FTRL的基础知识准备 part-1

前言

　　最近看了下在线学习FTRL的相关东东，对其背后的理论知识梳理下。
　　假设loss 函数为 f(x) ，其中 ft(xt) 表示第 t 轮数据，在第t轮参数 xt 所对应的损失。

xt+1=argminx∑t=1tft(x)

　　主要求证一个问题，上面这个取参数的策略在什么情况下有效？为什么有效？

1 评估函数 Regret

　　假设loss 函数为 f(x) ，其中 ft(xt) 表示第 t 轮数据所对应的loss函数。xt表示 t 轮数据时，预测模型所对应的参数。
　　那么，经过T轮数据后，每轮的损失叠加到一起，表示为：∑Tt=1ft(xt)
　　假设，有个全局最理想的参数 x∗ ，其对应的T轮数据后的，损失叠加到一起表示为： ∑Tt=1ft(x∗)
　　那么预测模型的经过T轮数据的损失总和与最理想状态的损失之和的差表示为：

Regret(x∗,ft)=∑t=1Tft(xt)−∑t=1Tft(x∗)=∑t=1Tft(xt)−f1:T(x∗)

　　我们通常用 Regret(x∗,ft) 来衡量预测模型的好坏，可以看到，其差是越小越好。
　　长远来看，平均的误差：

limT−>+∞Regret(x∗,ft)T

2 Regret Bound

　　 在loss函数和regular函数 ，(及其他约束函数) 选取得当的情况， Regret是有上限的。
　　 这里先给出Regret的两个上限，再然后予以证明。
　　1) General FTRL Bound
　　假设 rt使得h0:t+ft+1=r0:t+f1:t+1是1−strong−convexw.s.t||⋅||(t−1)
　　

Regret(x∗,ft)≤r0:T−1(x∗)+12∑t=1T||gt||2(t−1),∗

　　 2) FTRL - Proximal Bound
　　假设 rt使得h0:t=r0:t+f1:t是1−strong−convexw.s.t||⋅||(t)
　　

Regret(x∗,ft)≤r0:T(x∗)+12∑t=1T||gt||2(t),∗

　　证明在下一篇里《FTRL两个Regret上限的证明》。本篇主要讲解证明所需的基础知识。

3 基础知识

3.1 convex function(凸函数)

3.1.1 凸函数定义

　　凸是个重要概念。
　　凸集： ∀x,y∈集合S,xy之间的连线上的任意一点都在集合S内
　　非凸集： ∃x,y∈集合S,xy之间的连线上的某一点不在集合S内
　　一个函数是凸的当且仅当其上境图（在函数图像上方的点集）为一个凸集。
　　可以看到凸集是个连通域。
　
　　convex-fun数学定义： ∀x,y∈dom(f),θ∈[0,1];

f(θx−(1−θ)y)≤θf(x)+(1−θ)f(y)

　　 strict-convex 定义： ∀x,y∈dom(f),θ∈[0,1];

f(θx−(1−θ)y)<θf(x)+(1−θ)f(y)

　　 strong-convex 定义: ∀x,y∈dom(f),θ∈[0,1];
　　

f(θx−(1−θ)y)≤θf(x)+(1−θ)f(y)−m2θ(1−θ)||x−y||22,m>0

　 　　
　　 strong-convex 或定义： (f′(x)−f′(y))(x−y)≥m||x−y||22,m>0
　　 strong-convex 或定义： (f′(x)−f′(y))(x−y)≥m||x−y||22,m>0
　　 strong-convex 或定义： f(y)−f(x)≥f′(x)(y−x)+m2||x−y||22,m>0
　　strong-convex 则一定是 strict convex；
　　strict-convex 不一定是 strong-convex。
　　假设都存在二阶导数时：
　　 convex-fun 或定义： f′′(x)≥0
　　 strict-convex 或定义： f′′(x)>0
　　 strong-convex 或定义: f′′(x)≥m>0 　　

3.1.2 凸函数性质

导数grad和次导数subgrad。

　　连续可导的情况下：
　　一维时，连续可导函数 f(x) , 有导数 f′(x)=dfdx
　　多维时，连续可导函数 f(x,y) ，有梯度 grad=(∂f∂x+∂f∂y)
　　 l⃗ =(cos(α),cos(β)) 方向上， f(x,y) 有方向导数,

∂f(x,y)∂l=<grad,(cos(α),cos(β))>

　　 函数为凸函数时，若遇到连续不可导处，如何扩展导数的概念呢？
　　 次导数：subderivative 定义：
　　

f(y)−f(x)≥gx(y−x),∀y∈dom(f)

　　 其中gx为x处的次导数，其范围[a,b]，a=f′(x−)某点左侧导数;b=f′(x+)某点右侧导数

　　
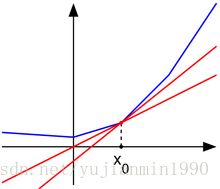
　　次微分：subdifferential
　　所有[a,b]范围内的次导数集合,称为x点处的次微分。
　　 次梯度：次微分的多维扩展。
　　

f(y)−f(x)≥<gx,(y−x)>,∀y∈dom(f)

　　其中所有向量 g 的集合，称为次梯度，记做∂f(x) 。
　　 注意到，
　　0）次梯度是对凸函数的导数的延伸。
　　1） ∂f(x) 是个封闭凸集。在连续可导时，为 ∂f(x)={dfdx} 。
　　2）最优解的充要条件：　
　　　　凸函数最值存在的条件： f(x∗)=minxf(x)⇔0∈∂f(x∗)
　　　　凸函数连续可导时条件： f(x∗)=minxf(x)⇔0=dfdx|x=x∗
　　　　 notice: 这里为后面更新参数时的最优封闭解的构造提供了思路。
　　3）次梯度仍然指示了下降的方向，跟梯度有异曲同工之妙。
　　　　假设 x2=x1−αg 迭代参数，会使得 x,x∗ 距离不断减小。
　　　　 ||x2−x∗||2≤||x1−x∗||2
　　　　　　　　　　 =||x1−x∗||2−2αgT(x1−x∗)+α2||g||2
　　　　　　　　　　 ≤||x1−x∗||2−2α(f(x1)−f(x∗))+α2||g||2
　　　　　　　　　　 ≤||x1−x∗||2
　　　　 notice:这里为次梯度下降法提供理论依据。

凸函数性质

　　对凸函数 f 而言，gx∈∂f(x),∀y∈dom(f)
　　有

f(y)−f(x)≥gx(y−x)

　　也即

f(x)−f(y)≤gx(x−y)

　　 这是个非常重要的性质，对Regret的右侧放缩，为何线性化近似损失 f(x) 为 gx 的理解非常重要。
　　对某一轮数据

ft(xt)−ft(x∗)≤gt(xt−x∗)

　　其中 x∗ 为凸函数的最优解， xt 为任意一个解， gt 为在 xt 处的一阶导数或者某个次梯度。 gt∈∂f(xt)
　　于是可得:

∑t=1Tft(xt)−ft(x∗)≤∑t=1Tgt(xt−x∗)

　　

Regret(x∗,ft)≤Regret(x∗,ft^),其中ft(x)^=gx

　　从而将general的convex-loss函数，根据其性质，将Regret的上限形式由loss凸函数f(x)转为另外更简单形式的loss函数的上限形式。

3.2 smooth function

　　函数上每一点满足： lim|h|→0|f(x+h)+f(x−h)−2f(x)||h|=0
　　则函数称为smooth function。

3.3 Lipschitz condition & Lipschitz constant

　　Lipschitz condition，用来描述连续模，满足LC，表示函数变化速度有限。
　　 f:[a,b]→R,若存在一个常数M,满足下式，则称f满足Lipschitz条件
　　

|f(y)−f(x)|≤M|y−x|

　　 Lipschitz constant，定义了最小的M>0。
　　

Lipschitz−constant=argminMM=supx≠y|f(y)−f(x)||y−x|

　　其中 sup 是最小上界的表示符号。

3.4 Dual Norm(对偶范数)

　　 ||⋅||为R上的的范数 ，则定义对偶范数 ||⋅||∗ 如下：
　　

||z||∗=sup{z∗x|||x||<1}

　　1-范数，||x||_1 = \sum_i | x_i |
　　1-范数的对偶范数 -> ∞−范数
　　 ||z||∗=sup{zx|||x||1≤1}=maxi|z[i]|=||z||∞
　　2-范数， ||x||2=∑i(xi)2−−−−−−−√
　　 2-范数的对偶范数 -> 2-范数，后面会频繁用到这一性质。
　　 ||z||∗=sup{zx|||x||2≤1}=supzx/||x||2=||z||2||x||2||x||2=||z||2
　　 ∞−范数 -> 1-范数的对偶范数.
　　p-范数， ||x||p=(∑i(xi)p)1/p
　　p-范数的对偶范数 -> q-范数，其中 1p+1q=1
　　notice： σ||⋅||2的对偶范数是1σ||⋅||2
　　 Rn 中向量 σ||⋅||2 的对偶范数， ||z||∗=sup{zx|σ||x||≤1}
　　 =sup{zxσ||x||2}=||z||2||x||2σ||x||2=1σ||z||2 ，这一性质会在后面频繁用到。

3.5 Legendre Transform 与 convex conjugate(凸共轭)

　　定义任意函数 y=f(x) ，直线函数 y=px ，定义两者的差如下：
　　

D(p,x)=px−f(x)

　　
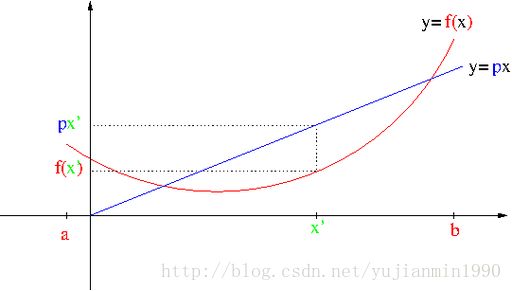
　　什么时候 D 取得最大值呢？
　　∂D∂x=0=p−dfdx
　　很明显，在 f(x) 上找到与 px 平行的切线时，取得最大差值。
　　 ∂D∂p=x 这个式子，则给出了D函数与x的关系。
　　这个式子，牛就牛在， 将f(x)与其导数的关系给联系起来。
　　若是我们一直取最大差，作为新的函数：

f∗(p)=supx{px−f(x)}

　　此时，将 f∗(p)称为f(x)的LegendreTransform
　　若 f(x) 是convex-function，则称 f∗(p)为f(x)的凸共轭(convex−conjugate)函数
　　当存在导数时： f∗=dfdxx−f(x)

3.6 relation between strong-smooth and strong-convex

3.6.1 α−strongly−convex 定义

　　 ∀x,y∈R；g∈∂f(x)
　　

f(y)−f(x)≥gx(y−x)+σ2||y−x||2

3.6.2 β−strongly−smooth 定义

　　 ∀x,y∈R

f∗(y)−f∗(x)≤▽f∗(x)(y−x)+12β||y−x||2∗

3.6.3 Duality relation between them

　　 f()is strongly−convexw.r.t||⋅||⇔ f∗()is strongly−smoothw.r.t||⋅||
　　 α−strongly−convexw.r.t||⋅||↔1α−strongly−smoothw.r.t||⋅||∗
　　简单感觉，就是将不等式的关系，通过LegendreTransform变换，翻了个跟头。
　　关系证明，见reference3第二篇paper。

4 reference

　　1. subgradient method 《2003-Subgradient Methods》
　　2. FTRL的两个上限《A Survey of Algorithms and Analysis for Adaptive Online Learning》
　　3. smooth&convex
　　《The Duality of Strong Convexity and Strong Smoothness Applications to Machine Learning》
　　《2009-On the duality of strong convexity and strong smoothness: Learning applications and matrix regularization》
　　4. 其他, wiki.
　　5. 数学概念网站, https://www.encyclopediaofmath.org/index.php/Main_Page