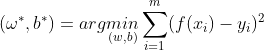机器学习-分类-线性分类器

在一个机器学习任务中，如果每一条数据的目标值是离散的，则该任务是一个分类任务。

解决分类问题基本的方法有：线性分类器、决策树、朴素贝叶斯、人工神经网络、K近邻（KNN）、支持向量机（SVM）；

组合基本分类器的集成学习算法：随机森林、Adaboost、Xgboost等。

一、线性分类器

线性分类器=假设函数+损失函数，假设函数是原始图像数据到类别的映射；

使用线性分类器分类的问题可以转化为最优化问题：通过更新假设函数的参数值来最小化损失函数的值，从而找到最优解。

在线性分类器中，输出是输入的加权和。

常用的线性分类器有：基本线性分类器、最小二乘线性分类器、感知器、逻辑回归分类器。

1.基本线性分类器

原理：

（1）计算目标值为1的所有正例数据的重心和目标值为0的所有负例数据的重心。

（2）计算与正例重心与负例重心距离相等的超平面。

过程：

（1）对训练集中目标值为1的正例逐个属性求均值，得到正例重心；对训练集中目标值为0的负例逐属性求均值，得到负例重心。

（2）正例重心和负例重心相减得到权重向量。

（3）将正例重心和负例重心相加除以2得到中点C。

（4）将T=作为分类阈值。对测试集的每个样本x与权重做点乘，若大于T，则分为1；否则分为0。

 python代码：

#1.基本线性分类器
class BaseLinearClassifier:
    def __init__(self,w=np.zeros((20,1))):
        #私有属性不允许继承
        self.weight=w
        
    #查看权重系数
    @property
    def get_weight(self):
        return self.weight
    
    #训练函数
    def fit(self,xtrain,ytrain):
        #得到正例索引
        index1=np.where(ytrain==1)
        #得到正例重心
        #axis=0表示“压缩行”，对各列求均值，最终得到1*n矩阵。
        pos_centriod=np.mean(xtrain[index1[0]],axis=0)
        
        #得到负例索引
        index2=np.where(ytrain==0)
        #得到负例重心
        neg_centriod=np.mean(xtrain[index2[0]],axis=0)

        #得到权重向量
        self.weight=pos_centriod-neg_centriod
        
        #计算阈值
        T=np.dot(self.weight,1/2*(pos_centriod+neg_centriod))
        
        return T
    
    #准确率测试
    def score(self,xtest,ytest,threshold):
        #测试集预测的类别
        predict=[]
        
        for i in xtest:
            #若大于阈值，则返回类别1
            if np.dot(i,self.weight)>=threshold:
                predict.append(1)
            #若小于阈值，则返回类别0
            else:
                predict.append(0)
        #计算准确率
        accuracy=accuracy_score(ytest, predict)
        return accuracy

#调用
baseLR=BaseLinearClassifier()
T=baseLR.fit(xtrain,ytrain)#返回阈值
accuracy_baseLR=baseLR.score(xtest,ytest,T)

2.最小二乘线性分类器

原理：

当预测值与真实值之间的均方误差最小时，预测值与真实值最接近。此时的与b即求解结果。

过程：

（1）把数据集D表示成一个m*(d+1)的矩阵X，每行对应一个样本，前d个元素对应样本的d个属性值，最后一个元素恒为1（把常数项b也合并进w中了）。

（2）此时的求解结果为：

（3）当满秩时，可以按照计算。

python代码：

#2.最小二乘线性分类器
import numpy.linalg as lin
class LsqClassifier(BaseLinearClassifier):
#在继承父类后，如果在子类中重新定义了和父类中名字一样的函数，则先执行子类的，当在子类中找不到时，才去父类中找。
    def __init__(self):
        super().__init__()#继承父类中的init属性
    
    #训练函数
    def fit(self,xtrain,ytrain):
        #按照最终得到的那个公式直接求出权重矩阵。
        XTX=np.matmul(xtrain.T,xtrain)#np.matmual函数用于矩阵相乘，这里计算出X{T}*X
        XTX_inv=lin.inv(XTX)#求矩阵的逆
        XTX_inv_XT=np.matmul(XTX_inv,xtrain.T)
        self.weight=np.dot(XTX_inv_XT,ytrain)
        
    #准确率测试
    def score(self,xtest,ytest,threshold=0):
        predict=[]
        for i in xtest:
            if np.dot(i,self.weight)>threshold:
                predict.append(1)
            else:
                predict.append(0)
        accuracy=accuracy_score(ytest, predict)
        return accuracy
    
    @property
    def get_weight(self):
        return self.weight

#调用
lsqLR=LsqClassifier()
lsqLR.fit(xtrain,ytrain)#返回阈值
accuracy_lsqLR=lsqLR.score(xtest,ytest)

3.感知器

原理：

假设有n个输入（每个样本有n个属性），将每个输入值加权求和，然后判断结果是否达到了某一个阈值v，若达到，则输出1；否则为-1。

现在令阈值v=-w_0，新增变量x_0=1，此时公式变为：

过程：

（1）随机初始化权重向量。

（2）对每个训练样本，按照公式计算其预期输出（符号函数的定义是，参数大于0时返回1；小于0时返回-1；等于0时返回0）。

（3）当预测值不等于真实值时，修改权重向量：，为更新步长，也叫学习速率。由于采用随机梯度下降，所以每次仅选取一个误分类样本来计算梯度。

（4）重复（2）（3），直到数据集没有被错分的样例。

python代码：

#3.感知器
class Perception(BaseLinearClassifier):
    def __init__(self,learning_rate=0.1):
        super().__init__(np.random.rand(20,1))
        self.learning_rate=learning_rate
        
    def fit(self,xtrain,ytrain):
        #找到训练集中所有正例
        indexes=np.where(ytrain==1)
        pos=xtrain[indexes[0],:]
        #对所有误分类样本进行权重学习，直到所有样本都分类正确，退出迭代；或者达到最大迭代次数，推出迭代。
        count=0
        for ite in range(500):#设置最大迭代次数为500
            for i in pos:
                if np.dot(i,self.weight)<0:#分类错误
                    self.weight+=self.__learning_rate*np.array(i).reshape(-1,1)
                    #reshape(-1,1)的意思是，我们并不知道原来数组的形状，但我们想让列数变为1列，如果在行的位置填入-1，那么系统会自动计算出需要多少行。
                else:#正确分类个数加1
                    count+=1
            if count==len(indexes[0]):#全部分类正确
                break
    def score(self,xtest,ytest,threshold=0):
        predict=[]
        for i in xtest:
            if np.dot(i,self.weight)>=0:
                predict.append(1)
            else:
                predict.append(0)
        accuracy=accuracy_score(ytest,predict)
        return accuracy
    @property
    def get_weight(self):
        return self.weight

#调用
perception=Perception()
perception.fit(xtrain,ytrain)
accuracy_perception=perception.score(xtest,ytest)

4.逻辑回归分类器

原理：

对于分类问题，需要一个函数能够通过所有的输入预测出类别。

考虑最简单的二分类情况，给定数据集。

利用线性回归模型计算得到预测值。

为了分类，需要将z转化为0和1。

考虑选取逻辑函数作为转化函数，将任意值映射到[0,1]，实现由值到概率的转换。

先从一条数据拟合的直线开始，沿着最大化可能性（最大化极大似然函数）的方向不断优化，最终求出模型参数。

过程：

（1）令则因为w为要求的参数，故去掉前面的负号，转换函数变为：

（2）有

（3）将y视为样本x为0类的概率，1-y视为样本x为1类的概率。二者的比值成为“几率”，一个事件的几率就是指该事件发生的概率与该事件不发生的概率的比值，反映了该事件发生的相对可能性。对几率取对数则得到对数几率（Logit）。

（4）若将y视为已知样本为x并且最终被分为0类的概率，即类后验概率p{y=0|x;w}。并且给出记号：p{y=1|x;w}=，则p{y=0|x;w}=1-，则有：

（5）在得到已知参数向量和所有训练样本的情况下，求得似然函数：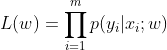

（6）

python代码：

sklearn库中有专门的逻辑回归分类器，直接调用即可。

#4.逻辑回归分类器
from sklearn.linear_model import LogisticRegression
lr=LogisticRegression()
lr.fit(xtrain,ytrain)
score=lr.score(xtest,ytest)