PyTorch使用教程-PyTorch构建神经网络(下)

PyTorch使用教程-PyTorch构建神经网络(下)

前言

上节我们使用了PyTorch自己组建了一个线性回归模型,并且我们自己实现了一个网络和优化,如果这些你都了解了那这节我们就能顺其自然的使用PyTorch给我们的封装来实现一个简单的DNN模型了

网络模型

一个简单的DNN应该有这三部分组成输入,隐藏,输出层

有个好玩的游乐场

可以自己组件DNN来拟合数据,其中的超参数有:
Learning rate:学习率,上节有讲到
Activation:激活函数,其作用让模型具有拟合非线性数据的能力
Regularization:正则化非常著名的有l1正则和l2正则,l1用于生成稀疏矩阵,而l2可以用来防止过拟合
Regularization rate:正则化的超参数
Problem type:选择模型是分类模型,还是回归模型

模型构建

1. 模型定义

import torch
from torch import nn
import torch.nn.functional as F
import torch.optim as optim
class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        self.fc1 = nn.Linear(in_features=1,out_features=128)
        self.fc2 = nn.Linear(in_features=128,out_features=1)
    def forward(self, inputs):
        x = F.relu(self.fc1(inputs))
        x = self.fc2(x)
        return x

类继承nn.Module类,这样我们的类就变成一个模型了,forward前向计算,并返回结果
2. 数据的准备(依然使用上节例子方便画出图像)

x = torch.rand(100, 1)
real_out = torch.tensor(10.) * x + torch.tensor(8) + torch.rand(100,1)

3. 准备优化器,计算损失,循环优化到最优值

dnn = DNN() #实例化模型,每实例化一个模型,那么参数是不相互共享的,是单独存在的
mse = nn.MSELoss() #实例化均方误差
adam = optim.Adam(lr=0.00001, params=dnn.parameters())
# 需要将需要优化的参数传入params中
for i in range(100000):
    pre_out = dnn(x) # 输入值,计算到预测值
    adam.zero_grad() # 清除梯度,为什要清除上节我们有讲到
    loss = mse(pre_out, real_out) # 计算均方误差
    loss.backward() # 自动求grad并累积到可训练参数中
    adam.step() # 执行最小化
    if (i+1) % 1000==0:
        print(loss)

上节自定义的优化,可以对比学习

for i in range(100000):
    pre_out = w * x + b
    loss = ((pre_out-real_out)**2).mean()
    loss.backward() # 自动求grad并累积到可训练参数grad中
    w.data = w.data - lr*w.grad.data # 执行最小化
    b.data = b.data - lr*b.grad.data # 执行最小化
    w.grad.data = torch.tensor(0.) # 清除梯度
    b.grad.data = torch.tensor(0.) # 清除梯度
    if (i+1) % 10000==0:
        print(loss)

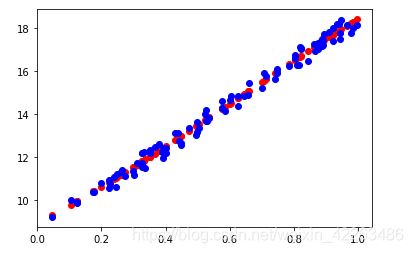
拟合效果的展示

import matplotlib.pyplot as plt
pre_out = dnn(x)
plt.scatter(x.detach().numpy(), pre_out.detach().numpy(), c='r')
plt.scatter(x.detach().numpy(), real_out.detach().numpy(), c='b')
plt.show()

总结

这节我们使用了,torch自带的函数帮助我们实现梯度下降,找梯度的最小值,是不是非常顺利的就可以理解了呢?

上节回顾

PyTorch使用教程-PyTorch构建神经网络(上)

预习

小试牛刀实现手写数字识别器