决策树——依据水果特征分类

一、获取数据集

水果中苹果和杨桃外部特征比较鲜明，例如下面两张苹果、杨桃图片，苹果颜色为红色、形状大致为椭圆形、表面光滑没有棱角、带叶子，杨桃则是黄色、五角星形、带有棱角、没叶子。

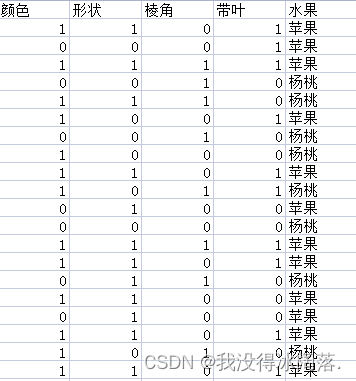
利用上述特征统计一些苹果和杨桃数据：

• 颜色： 1-红色 0-黄色
• 形状： 1-椭圆形 0-五角星形
• 棱角： 1-有棱角 0-无棱角
• 带叶： 1-带叶子 0-不带叶子

1、提取数据

利用CSV库将指定特征分类，将除去第一行的数据提取出来，作为本次实验的数据集

其中第一行就是决策树的每一个节点，存到lables中；再将特征对应每一种情况存到了labels中。

# 获取数据集
def createDataSet(filename):
    # 读取文件
    data = open(filename, 'rt', encoding='gbk')
    reader = csv.reader(data)
    # 获取标签列
    handlers = next(reader)
    lables = handlers[:-1]
    # 数据列表
    dataSet = []

    for row in reader:
        # 读取除第一行的数据
        dataSet.append(row[:])
        
    # 特征对应的所有可能的情况
    labels_full = {}
    for i in range(len(lables)):
        labelList = [example[i] for example in dataSet]
        uniqueLabel = set(labelList)
        labels_full[lables[i]] = uniqueLabel
    return dataSet, lables, labels_full

2、划分数据

dataSet输入的数据，axis是labels中对应坐标，value是对应属性下的属性值。

# 划分数据集  
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        # 给定特征值等于想要的特征值
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            # 将该特征值后面的内容保存起来
            reducedFeatVec.extend(featVec[axis + 1:])
            retDataSet.append(reducedFeatVec)

    return retDataSet
print(splitDataSet(dataSet, 1, '0'))

利用majorityCnt方法获取一个集合中，出现次数最多的标签

# 获取出现次数最多的类别
def majorityCnt(classList):
    classCount = collections.defaultdict(int)
    # 遍历所有的类别
    for vote in classList:
        classCount[vote] += 1
    # 降序排序，第一行第一列就是最多的
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

二、计算信息增益

1、信息熵

首先获取全部数据长度，再创建一个字典，键值是最后一列数值。每个键值记录了当前类别出现的次数，最后算出所有类标签的发生评率计算类别出现的评率，最后计算熵值。

# 获取水果信息熵
def calcShannonEnt(dataSet):
    # 总数
    numEntries = len(dataSet)
    # 用来统计标签
    labelCounts = collections.defaultdict(int)
    # 循环整个数据集，得到数据的分类标签
    for featVec in dataSet:
        # 得到当前的标签
        currentLabel = featVec[-1]
        labelCounts[currentLabel] += 1
    # 计算信息熵
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob, 2)
    return shannonEnt

2、计算信息增益

计算信息增益首先获取所有特征的种数，不包含最后水果分类；再计算每个特征对应信息熵；最后将分类的信息熵减去该特征的信息熵，就是对应特征的信息增益。获取到每个特征的信息增益之后，将最大值对应的标签下标返回，在构建决策树时作为数的根节点。
每个特征对应的信息增益，最后返回最大标签对应下标：

# 计算每个特征信息增益
def chooseBestFeatureToSplit(dataSet, labels):
    # 特征数 总的列数减去最后的一列
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    # 对每个特征值进行求信息熵
    for i in range(numFeatures):
        # 得到数据集中所有的当前特征值列表
        featList = [example[i] for example in dataSet]
        # 当前特征值中共有多少种
        uniqueVals = set(featList)
        newEntropy = 0.0

        # 遍历现在有的特征的可能性
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value)
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy

        print( labels[i] + '信息增益值为：' + str(infoGain))
        # 找出最大的值
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature
print(chooseBestFeatureToSplit(dataSet, lables))

三、绘制决策树

输入数据集和标签数组，能够得到一个类似字典的决策树。
首先拿到所有数据集的分类标签，再统计第一个标签出现的次数，与总标签个数比较。计算第一行有多少个数据，如果只有一个的话说明所有的特征属性都遍历完了，剩下的一个就是类别标签，或者所有的样本在全部属性上都一致，然后利用majorityCnt返回剩下标签中出现次数较多的那个。在利用chooseBestFeatureToSplit选择最好的划分特征，得到该特征的下标，作为根节点。最后递归调用，将数据集中该特征等于当前特征值的所有数据划分到当前节点下，递归调用时需要先将当前的特征去除掉。

# 绘制决策树
def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    print(classList)
    # 统计第一个标签出现的次数，与总标签个数比较
    if classList.count(classList[0]) == len(classList):
        return classList[0]

    if len(dataSet[0]) == 1 :
        # 返回剩下标签中出现次数较多的那个
        return majorityCnt(classList)

    bestFeat = chooseBestFeatureToSplit(dataSet=dataSet, labels=labels)
    bestFeatLabel = labels[bestFeat]

    myTree = {bestFeatLabel: {}}

    # 将本次划分的特征值从列表中删除掉
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)

    # 遍历所有的特征值
    for value in uniqueVals:
        subLabels = labels[:]
        subTree = createTree(splitDataSet(dataSet=dataSet, axis=bestFeat, value=value), subLabels)
        # 递归调用
        myTree[bestFeatLabel][value] = subTree
    return myTree
print(createTree(dataSet, lables))

获取一个字典形状的决策树：

{'带叶': 
    {'1': {'形状': 
            {'1': '苹果', 
            '0': {'棱角': 
                {'1': '杨桃', 
                 '0': '苹果'}}}}, 
     '0': {'棱角': 
            {'1': '杨桃', 
             '0': {'颜色': 
                {'1': {'形状': {'杨桃': '杨桃', '苹果': '苹果'}}, 
                 '0': {'形状': {'杨桃': '杨桃', '苹果': '苹果'}}}}}}}}

四、分类预测

分类预测也是一个递归函数，使用index方法查找当前列表中第一个匹配firstStr变量的元素。然后递归遍历整棵树，比较testVec变量中的值和树节点的值，若达到叶子节点就返回分类标签。

# 预测
def classify(inTree, featLabel, testVec):
    # 获取第一个节点
    firstStr = list(inTree.keys())[0]
    secondDict = inTree[firstStr]
    # 节点对应下标
    featIndex = featLabel.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            # 递归判断
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key], featLabel, testVec)
            else: classLabel = secondDict[key]
    # 返回预测
    return classLabel

测试结果：

代码：
链接：https://pan.baidu.com/s/1gjbXKDworG7ejzS6cCTvgQ?pwd=kupj
提取码：kupj