机器学习-评价指标总结

分类指标

错误率与精度

在分类任务中，即预测离散值的问题，最常用的是错误率和精度，错误率是分类错误的样本数占样本总数的比例，精度则是分类正确的样本数占样本总数的比例，易知：错误率+精度=1。

对样例集 D ， 分类错误率定义为（等概率）:

或（有概率分布的）

精度则定义为（等概率）：

或（有概率分布的）

参考文章

• 机器学习（西瓜书）-模型评估与选择
• 精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？
• 机器学习评估指标
• 你知道这11个重要的机器学习模型评估指标吗?
• 机器学习模型评估指标汇总
• 性能指标（模型评估）之mAP
• 机器学习分类模型评价指标详述
• 机器学习评价指标
• 面试官如何判断面试者的机器学习水平？

查准率、查全率与Fl

1. 查准率和查全率

错误率和精度虽然常用，但不能满足所有的需求，例如：在推荐系统中，我们只关心推送给用户的内容用户是否感兴趣（即查准率），或者说所有用户感兴趣的内容我们推送出来了多少（即查全率）。因此，使用查准/查全率更适合描述这类问题。对于二分类问题，分类结果混淆矩阵与查准/查全率定义如下：

查准率 P（学习器分类的正例中判断正确的比例） ：

查全率 R （所有的正例中学习器判断正确的比例）：

2. P-R曲线

正如天下没有免费的午餐，查准率和查全率是一对矛盾的度量。例如我们想让推送的内容尽可能用户全都感兴趣，那只能推送我们把握高的内容，这样就漏掉了一些用户感兴趣的内容，查全率就低了（比较收敛）；如果想让用户感兴趣的内容都被推送，那只有将所有内容都推送上，宁可错杀一千，不可放过一个，这样查准率就很低了（比较开放）。

“P-R曲线”正是描述查准/查全率变化的曲线，P-R曲线定义如下：根据学习器的预测结果（一般为一个实值或概率）对测试样本进行排序，将最可能是“正例”的样本排在前面，最不可能是“正例”的排在后面，按此顺序逐个把样本作为“正例”进行预测，每次计算出当前的P值和R值，如下图所示：

P-R曲线如何评估呢？

1、若一个学习器A的P-R曲线被另一个学习器B的P-R 曲线完全包住，则称：B的性能优于A。
2、若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。
3、但一般来说，曲线下的面积是很难进行估算的，所以衍生出了“平衡点”（Break-Event Point，简称BEP），即当P=R时的取值，平衡点的取值越高，性能更优。

3. 标准的F1

P和R指标有时会出现矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure，又称F-Score。F-Measure是P和R的加权调和平均：

其中 $\beta$>0 度量了查全率对查准率的相对重要性。

$\beta$ = 1时，退化为标准的 F1；
$\beta$> 1 时查全率有更大影响；
$\beta$< 1 时查准率有更大影响。

4. 宏F1和微F1

有时候我们会有多个二分类混淆矩阵，例如：多次训练或者在多个数据集上训练，那么估算全局性能的方法有两种，分为宏观和微观。

简单理解，宏观就是先算出每个混淆矩阵的 P 值和 R 值，也就是先在各混淆矩阵上分别计算出查准率 P 和查全率 R，然后取得平均 P 值 macro-P（宏查准率） 和平均 R 值 macro-R（宏查全率），再算出 $F_{\beta }$ 或 F1（宏F1），

微观则是计算出混淆矩阵的平均$\overline{TP}$、$\overline{FP}$、$\overline{TN}$、$\overline{FN}$，也就是先对各混淆矩阵对应元素（TP、FP、FN、TN）求平均，接着进行计算micro-P（微查准率）、micro-R（微查全率），进而求出 $F_{\beta }$ 或 micor-F1（微F1）。

参考文章

• 机器学习（西瓜书）-模型评估与选择

ROC与AUC

1. TPR、FPR和ROC曲线

学习器对测试样本的评估结果一般为一个实值或概率，设定一个阈值，大于阈值为正例，小于阈值为负例，因此这个实值的好坏直接决定了学习器的泛化性能，若将这些实值排序，则排序的好坏决定了学习器的性能高低。ROC曲线正是从这个角度出发来研究学习器的泛化性能。

ROC曲线与P-R曲线十分类似，都是按照排序的顺序逐一按照正例预测，不同的是ROC曲线以 “真正例率” （True Positive Rate，简称TPR）为横轴，

以 “假正例率” （False Positive Rate，简称FPR）为纵轴，

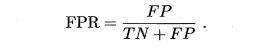
ROC偏重研究基于测试样本评估值的排序好坏。

简单分析图像，可以得知：当FN=0时，TN也必须0，反之也成立，我们可以画一个队列，试着使用不同的截断点（即阈值）去分割队列，来分析曲线的形状，

（0,0）表示将所有的样本预测为负例，
（1,1）表示将所有的样本预测为正例，
（0,1）表示正例全部出现在负例之前的理想情况，
（1,0）则表示负例全部出现在正例之前的最差情况。
限于篇幅，这里不再论述，主要心中有表2.1，P-R曲线和ROC曲线都是以这个表为基础的。

2. ROC曲线绘制方法

现实任务中通常是利用有限个测试样例来绘制 ROC 图，此时仅能获得有限个(真正例率，假正例率)坐标对，无法产生图 2.4(a) 中的光滑 ROC 曲线 ， 只能绘制出如图 2.4(b)所示的近似 ROC 曲线。

绘图过程很简单：
1、给定 $m^{+}$ 个正例和 $m^{-}$ 个反例，根据学习器预测结果对样例进行排序，然后把分类阈值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为 0 ， 在坐标 (0， 0) 处标记一个点；
2、然后将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例，设前一个标记点坐标为 $(x，y)$， 当前若为真正例，则对应标记点的坐标为 $(x,y+\frac{1}{m^{+}})$（真正例率TPR增加一点儿）；当前若为假正例，则对应标记点的坐标为 $(x+\frac{1}{m^{-}},y)$（假正例率FPR增加一点儿） ，然后用线段连接相邻点即得。

3. AUC计算方法

同样地，进行模型的性能比较时：
1、若一个学习器A的ROC曲线被另一个学习器B的ROC曲线完全包住，则称B的性能优于A。
2、若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。

ROC曲线下的面积定义为AUC（Area Under ROC Curve），不同于P-R的是，这里的AUC是可估算的，即ROC曲线下每一个小矩形的面积之和。易知：AUC越大，证明排序的质量越好，AUC为1时，证明所有正例排在了负例的前面（点(0,1)位置，最优），
AUC为0时，所有的负例排在了正例的前面（点（1,0）位置，最差）。

上图就是利用微积分原理估算AUC面积公式。

4. AUC和ROC曲线之上的面积 ${\ell }_{rank}$ 的关系

给定 m十个正例和 m 个反例，令 D+ 和 D-分别表示正、反例集合，
则排序损失 (loss)定义为

即考虑每一对正、反例，若正例的预测值小于反例，则记一个"罚分”；相等则记 0.5 个"罚分"容易看出 ， ${\ell }_{rank}$ 对应的是 ROC 曲线之上的面积。

AUC 和 ${\ell }_{rank}$ 有以上关系，两个代表的都是ROC曲线中的面积，与精确率和误差率的关系类似。

思考：
AUC会不会出现小于0.5的情况，出现了怎么调BUG
AUC小于0.5，说明分类器总是把对的预测成错的，错的预测成对的，说明类别弄反了，把类别顺序换下即可。

参考文章

• 机器学习（西瓜书）-模型评估与选择
• ROC曲线-阈值评价标准
• 机器学习面试题集-如何画 ROC 曲线
• ROC原理介绍及利用python实现二分类和多分类的ROC曲线
• 用Python绘制ROC曲线
• 为什么AUC一定会大于0.5？
• AUC ROC有可能等于1 吗？

P-R曲线和ROC曲线的区别

当正负样本的分布发生变化时，ROC 曲线的形状能够基本保持不变，而 P-R 曲线的形状一般会发生较剧烈的变化。

想要验证这个结论，可以先根据数据画出一对 ROC 和 PR 曲线，再将测试集中的负样本数量增加 10 倍后再画一对 ROC 和 PR 图，然后会看到 P-R 曲线发生了明显的变化，而 ROC 曲线形状基本不变。

这样，在评价一个模型的表现时，如果选择了不同的测试集进行评价，那么 ROC曲线可以更稳定地显示出模型的性能。

这个特点的实际意义

例如计算广告领域中的转化率模型，正样本的数量可能只是负样本数量的 1/1000 甚至 1/10000，这时若选择不同的测试集，ROC 曲线能够更加稳定地反映模型的好坏。

ROC 的这种稳定性使得它的应用场景更多，被广泛用于排序、推荐、广告等领域。

既然ROC更稳定，那要 PR 做什么？

当我们希望看到模型在某个特定数据集上的表现时，P-R 曲线能够更直观地反映模型性能。

参考文章

• 机器学习面试题集-如何画 ROC 曲线

AUC有没有更快的计算方法

1. AUC究竟指的是什么？

AUC其实就是随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。

具体关于AUC含义的分析可参考知乎上的解答，点击这里如何理解机器学习和统计中的AUC？。

2. 如何计算AUC

计算AUC时，推荐2种方法。

2.1 方法1

在有M个正样本，N个负样本的数据集里。一共有MN对样本（一对样本对即，一个正样本与一个负样本）。统计这MN对样本里，正样本的预测概率大于负样本的预测概率的个数。


举例说明：

ID	label	pro
A	0	0.1
B	0	0.4
C	1	0.35
D	1	0.8

假设有4条样本。2个正样本，2个负样本，那么M*N=4。即总共有4个样本对。分别是：（D,B）,（D,A）,(C,B),（C,A）。

在（D,B）样本对中，正样本D预测的概率大于负样本B预测的概率（也就是D的得分比B高），记为1；
同理，对于（C,B）。正样本C预测的概率小于负样本C预测的概率，记为0；
最后可以算得，总共有3个符合正样本得分高于负样本得分，故最后的AUC为：

在这个案例里，没有出现得分一致的情况，假如出现得分一致的时候，例如：

ID	label	pro
A	0	0.1
B	0	0.4
C	1	0.4
D	1	0.8

同样本是4个样本对，对于样本对（C,B）其 $I$ 值为 0.5。

最后的AUC为：

2.2 方法2

另外一个方法就是利用下面的公式：

这个公式看起来有点吓人，首先解释一下每一个符号的意思，公式的含义解释见： 公式解释-AUC计算方法总结

其中，$ran{k}_{in{s}_i}$ 代表第 $i$ 条样本的序号。（概率得分从小到大排，排在第 rank 个位置），$M,N$ 分别是正样本的个数和负样本的个数，${\sum }_{in{s}_i}\in positiveclass$ 只把正样本的序号加起来。

同样本地，我们用上面的例子解释下公式怎么计算的：

ID	label	pro
A	0	0.1
B	0	0.4
C	1	0.35
D	1	0.8

将这个例子排序。按概率排序后得到：

ID	label	pro	rank
A	0	0.1	1
C	1	0.35	2
B	0	0.4	3
D	1	0.8	4

按照上面的公式，只把正样本的序号加起来也就是只把样本C和D的rank值加起来后减去一个常数项：

即：

可以看出，该答案和方法1的计算结果是一样的。

这个时候，我们有个问题，假如出现得分一致的情况怎么办？下面举一个例子说明：

ID	label	pro
A	1	0.8
B	1	0.7
C	0	0.5
D	0	0.5
E	1	0.5
F	1	0.5
G	0	0.3

在这个例子中，我们有4个取值概率为0.5，而且既有正样本也有负样本的情况。计算的时候，其实原则就是相等得分的rank取平均值。具体来说如下：

先排序：

ID	label	pro	rank
G	0	0.3	1
F	1	0.5	2
E	1	0.5	3
D	0	0.5	4
C	0	0.5	5
B	1	0.7	6
A	1	0.8	7

这里需要注意的是：相等概率得分的样本，无论正负，谁在前，谁在后无所谓。

由于只考虑正样本的rank值：
对于正样本A，其rank值为7
对于正样本B，其rank值为6
对于正样本E，其rank值为（5+4+3+2）/4
对于正样本F，其rank值为（5+4+3+2）/4

最后我们得到：

以上解答参考AUC的计算方法这篇文章，该文章最后也提供了 Python 计算 AUC 的示例验证代码。

另外，还可参考图解AUC和GAUC这篇文章介绍的 AUC 计算图解，思路与方法1一致，十分推荐！

参考文章

• AUC的计算方法
• AUC计算方法总结
• 如何理解机器学习和统计中的AUC？
• AUC计算方法总结
• 图解AUC和GAUC

AUC值为1可能是由什么原因导致的

ROC 曲线的横轴是 FPR（假阳性率），纵轴是 TPR（真阳性率）。ROC曲线是一个单调递增的曲线。当AUC等于1时，ROC曲线将经过 (0,1) 点，即 FPR=0时，ROC曲线对应的 TPR=1，也就是说这时需存在一个阈值可以将所有的负样本预测为负样本，所有的正样本预测为正样本。

在一些实际中的简单测试集上是可以找到这样的阈值的，从理论上和在现实中均有AUC等于1的可能性出现。

参考文章

• AUC ROC有可能等于1 吗？

AUC为什么对正负样本分布不敏感

AUC表示ROC曲线下的面积，计算表达式如下：


注意：和准确率、召回率、F1值等依赖于判决阈值的评估指标相比，AUC则没有这个问题。AUC关心的是样本间的相对顺序，与模型为每一个样本输出的绝对分值没有关系，并且不易受正负样本数量变化的影响，因而是点击率预估模型中（搜索和推荐等场景）最重要的离线评价指标之一。

除了上述几何定义外，AUC还有一层概率含义，即随机从正负样本中选取一对正负样本，模型对正样本的得分高于负样本的概率。这个结论是可以证明的。具体证明过程可参考AUC为啥对正负样本比例不敏感？这篇文章。

这个问题的本质原因，在于横轴 FPR 只关注负样本，与正样本无关；纵轴 TPR 只关注正样本，与负样本无关。所以横纵轴都不受正负样本比例影响，积分当然也不受其影响。

思考：
如果对负样本进行采样，AUC的计算结果会发生变化吗？

参考文章

• AUC为啥对正负样本比例不敏感？
• 深入理解AUC——从概率意义的角度
• 深入理解AUC
• 对准确率、精确率、召回率、AUC、ROC的理解
• 为什么 AUC 对测试集上的类分布变化是不敏感的？
• AUC计算及为何不受样例不均衡的影响
• 为什么ROC曲线不受样本不均衡问题的影响
• AUC：直观理解AUC为何会对正负样本数分布不均匀情况鲁棒
• CTR 预测理论（十五）：分类评价指标 AUC 总结（优缺点、计算公式推导）
• 机器学习模型构建时正负样本不平衡带来的问题及解决方法

Group AUC（GAUC）

AUC在传统的机器学习二分类中还是很能打的，但是有一种场景，虽然是分类模型，但是却不适用AUC，即广告推荐领域。

推荐领域使用的CTR（点击率）来作为最终的商用指标，但是在训练推荐模型时，却不用这个指标，用的是GAUC，为什么呢，因为推荐模型目前比较成熟的模式是训练分类模型，这个分类模型的任务是预测用户是否会点击给定的商品，因此，推荐系统的核心，仍然是一个二分类问题，但是是更细力度的二分类。

总结：传统的AUC可以评判二分类，但是推荐领域要算的是对于每个人的二分类结果

给定如下情形：

我们准备训练一个模型用来预测用户A和用户B购买iphone、华为和小米的可能性，我们训练了模型α

对于所有出现的概率值：我们可以计算得到AUC为 $\frac{2+2+1}{2\ast 3}=0.833$ ，好像预测效果不太好。但是，如果对每个用户查看AUC，则有：

用户A auc：$\frac{1}{1\ast 1}=1$
用户B auc： $\frac{1}{1\ast 1}=1$

也就是说这个模型其实预测地很完美！

AUC的计算过程参考：
正样本：0.5，0.4，0.2
负样本：0.3，0.1
正样本3个，负样本2个，正负组合32=6种，
正样本值0.5大于负样本0.3、0.1 有两种，
正样本值0.4大于负样本0.3、0.1 有两种，
正样本值0.2大于负样本0.1 有一种，
所以正样本值大于负样本值的有2+2+1=5
所有AUC为5/6=0.833 。
GAUC计算过程参考：
用户A的正样本0.5，负样本0.3，所以GAUC为1；
用户B的正样本0.4，0.2，负样本0.1，正负组合为21种，正样本值大于负样本值有2种，
所以GAUC为1

所以传统的AUC在这种情况下失效了，由此引入了GAUC来从更细的力度上评估分类结果。

AUC反映的是整体样本间的一个排序能力，而在计算广告领域，我们实际要衡量的是不同用户对不同广告之间的排序能力，因此实际应该更关注的是同一个用户对不同广告间的排序能力。

GAUC（Group AUC）实际是计算每个用户的AUC，然后加权平均，最后得到Group AUC，这样就能减少不同用户间的排序结果不太好比较这一影响。

group auc具体公式如下：

实际处理时权重一般可以设为每个用户 view 或 click 的次数，而且会过滤掉单个用户全是正样本或负样本的情况。

以上回答来自知乎~

参考文章

• 机器学习算法评价指标之group auc（gauc）
• 图解AUC和GAUC
• 推荐系统评价指标：AUC和GAUC

F1和AUC有什么区别

1. 定义上的区别

AUC的优化目标：TPR和(1-FPR)
F1的优化目标：recall和precision

这里解释一下为什么 AUC 的优化目标是TPR和(1-FPR)。

大家知道AUC指的是ROC曲线下的面积大小。而ROC曲线是由TPR和FPR为轴的曲线。如果希望auc更大，那么在给定TPR的情况下，我们是希望FPR越小越好的，同样给定FPR，希望TPR越大越好，这样才能给曲线拉向对角线上方。所以我们可以认为：优化AUC就是希望同时优化TPR和(1-FPR)。另外，TPR又被成为sensitivity(灵敏度)，(1-FPR)又被成为specificity(特异度)

优化F1就是希望同时优化recall和precision这个比较好理解，因为F1的计算公式就是：
$$F1score=\frac{2\ast recall\ast precision}{recall+precision}$$

2. 两者的关系

相同点：
分析的起点是这两个指标存在一个共同目标。事实上：
$$recall=TPR=\frac{TP}{TP+FN}$$

也就是说 AUC 和 F1 score 都希望将样本中实际为真的样本检测出来(检验阳性)。

不同点：

区别就在于 AUC 除了希望提高 recall 之外，另一个优化目标是：
$$specificity=1-FPR=\frac{TN}{FP+TN}$$

希望提高非真样本在检验中呈阴性的比例，也就是降低非真样本呈阳性的比例(假阳性)，也就是检验犯错误的概率。

而 F1score 的另一个优化目标是：
$$precision=\frac{TP}{TP+FP}$$

希望提高检验呈阳性的样本中实际为真的比例，也就是提高检验的准确率/命中率。

那么说到这里，大家应该可以理解这里两个指标在 recall 之外，其实是存在内在矛盾的。如果说召回率衡量我们训练的模型(制造的一个检验)对既有知识的记忆能力(召回率)，那么两个指标都是希望训练一个能够很好拟合样本数据的模型，这一点上两者目标相同。但是 AUC 在此之外，希望训练一个尽量不误报的模型，也就是知识外推的时候倾向保守估计，而 F1 希望训练一个不放过任何可能的模型，即知识外推的时候倾向激进，这就是这两个指标的核心区别。

3. 不同情况怎么选择指标

在实际中，F1和AUC选择哪一个，需要做trade-off。如果我们犯检验误报错误的成本很高，那么我们选择 AUC 是更合适的指标。如果我们犯有漏网之鱼错误的成本很高，那么我们倾向于选择 F1score。

比如，对于检测传染病，相比于放过一个可能的感染者，我们愿意多隔离几个疑似病人，所以优选选择 F1score 作为评价指标。而对于推荐这种场景，由于现在公司的视频或者新闻库的物料总量是很大的，潜在的用户感兴趣的 item 有很多，所以我们更担心的是给用户推荐了他不喜欢的视频，导致用户体验下降，而不是担心漏掉用户可能感兴趣的视频。所以推荐场景下选择 AUC 是更合适的。

小结：
1）F1希望训练出一个不放过任何一种可能的模型。比如欺诈检测、癌症检测，漏诊是不负责的，宁可错杀一千，也不放过一个
2）AUC希望训练出一个尽量不误报的模型。比如推荐场景，推荐错了用户会非常反感
3）大部分场景都不能直接根据ACC来评价模型

参考文章

• 深入理解实际场景下 AUC vs F1 的区别——不说废话
• 精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？
• F1,AUC的区别与选择

回归指标

交叉熵跟MSE有什么区别

1. 适用场景不同

一般来说，平方损失函数（MSE）更适合输出为连续，并且最后一层不含 sigmoid 或 softmax 激活函数的神经网络；交叉熵损失则更适合二分类或多分类的场景。

1.1 分类问题中常用 cross entropy 而不用 MSE 的原因

解释角度1

在回归问题中，我们常常使用均方误差（MSE）作为损失函数，其公式如下：

其实这里也比较好理解，因为回归问题要求拟合实际的值，通过MSE衡量预测值和实际值之间的误差，可以通过梯度下降的方法来优化。而不像分类问题，需要一系列的激活函数（sigmoid、softmax）来将预测值映射到0-1之间，这时候再使用MSE的时候就要好好掂量一下了，为啥这么说，请继续看：

MSE + Sigmoid 的基本公式：

梯度求导过程：

上面复杂的推导过程，其实结论就是下面一张图：

其中，$C$ 就是的 $J$，$\sigma$ 就是 sigmoid 函数，$a$ 表示predict值。

从以上公式可以看出，$w$ 和 $b$ 的梯度跟激活函数的梯度成正比，激活函数的梯度越大，$w$ 和 $b$ 的大小调整得越快，训练收敛得就越快。而我们都知道 sigmoid 函数长这样：

在上图的绿色部分，初始值是0.98，红色部分初始值是0.82，假如真实值是0。直观来看那么0.82下降的速度明显高于0.98，但是明明0.98的误差更大，这就导致了神经网络不能像人一样，误差越大，学习的越快。

但是如果我们把MSE换成交叉熵会怎么样呢？

其中，$x$ 表示样本，$n$ 表示样本的总数。

重新计算梯度：


另外sigmoid有一个很好的性质：

我们从结果可以看出梯度中不再含有sigmoid的导数，有的是sigmoid的值和实际值之间的差，也就满足了我们之前所说的错误越大，下降的越快。这也就是在分类问题中常用cross entropy 而不是 MSE的原因了。

小结：
1）使用MSE作为损失函数，它的梯度和sigmod函数的导数有关，如果当前模型的输出接近0或者1时，就会非常小，接近0，使得求得的梯度很小，损失函数收敛的很慢；
2）使用交叉熵作为损失函数，它的导数就是一个差值（线性的），误差大的话更新的就快，误差小的话就更新的慢点，这正是我们想要的（不会存在学习速率过慢的问题）。

解释角度2

MSE实际上是高斯分布的最大似然，交叉熵是多项式分布的最大似然。

因为多分类问题的分布符合多项式分布，而二分类问题的分布符合伯努利分布（二项分布），所以分类问题当然得用多项式分布。

参考文章

• 简单的交叉熵，你真的懂了吗？
• 为什么LR模型损失数使用交叉熵不用MSE？
• 交叉熵损失函数原理详解
• 神经网络损失函数中怎样选择交叉熵和MSE，两者区别是什么？

排序指标

介绍下NDCG

1. NDCG是什么

NDCG的全称是：Normalized Discounted Cumulative Gain(归一化折损累计增益)

在搜索和推荐任务中，系统常返回一个item列表。如何衡量这个返回的列表是否优秀呢？

例如，当我们检索【推荐排序】，网页返回了与推荐排序相关的链接列表。列表可能会是[A,B,C,G,D,E,F],也可能是[C,F,A,E,D]，现在问题来了，当系统返回这些列表时，怎么评价哪个列表更好？

没错，NDCG就是用来评估排序结果的。搜索和推荐任务中比较常见。

2. 理解NDCG计算公式：G-CG-DCG-NDCG

2.1 G：增益

Gain: 表示一个列表中所有item的相关性分数。rel(i)表示item(i)相关性得分。

2.2 CG：累计增益

Cumulative Gain：表示对K个item的Gain进行累加。

CG只是单纯累加相关性，不考虑位置信息。

如果返回一个list_1=[A,B,C,D,E]，那list_1的CG为0.5+0.9+0.3+0.6+0.1=2.4
如果返回一个list_2=[D,A,E,C,B]，那list_2的CG为0.6+0.5+0.1+0.3+0.9=2.4
所以，顺序不影响CG得分。如果我们想评估不同顺序的影响，就需要使用另一个指标DCG来评估。

2.3 DCG：折损累计增益

Discounted Cumulative Gain：考虑排序顺序的因素，使得排名靠前的item增益更高，对排名靠后的item进行折损。

CG与顺序无关，而DCG评估了顺序的影响。DCG的思想是：list中item的顺序很重要，不同位置的贡献不同，一般来说，排在前面的item影响更大，排在后面的item影响较小。（例如一个返回的网页，肯定是排在前面的item会有更多人点击）。所以，相对CG来说，DCG使排在前面的item增加其影响，排在后面的item减弱其影响。

怎么实现这个思想呢？DCG在CG的基础上，给每个item的相关性比上log2(i+1)，i越大，log2(i+1)的值越大，相当于给每个item的相关性打个折扣，item越靠后，折扣越大。

还是上面那个例子：
list_1=[A,B,C,D,E], 其对应计算如下：

i	rel(i)	log(i+1)	rel(i)/log(i+1)
1 = A	0.5	1	0.5
2 = B	0.9	1.59	0.57
3 = C	0.3	2	0.15
4 = D	0.6	2.32	0.26
5 = E	0.1	2.59	0.04

list_1的 DCG_1= 0.5+0.57+0.15+0.26+0.04=1.52

list_2=[D,A,E,C,B]，其对应计算如下：

i	rel(i)	log(i+1)	rel(i)/log(i+1)
1 = D	0.6	1	0.6
2 = A	0.5	1.59	0.31
3 = E	0.1	2	0.05
4 = C	0.3	2.32	0.13
5 = B	0.9	2.59	0.35

list_2的 DCG_2= 0.6+0.31+0.05+0.13+0.35=1.44

DCG_1 > DCG_2, 所以在这个例子里list_1优于list_2。

到这里，我们可以知道，使用DCG方法就可以对不同的list进行评估，那为什么后面还有一个NDCG呢？

2.4 NDCG(Normalized DCG): 归一化折损累计增益

在NDCG之前，先了解一些IDGC(ideal DCG)–理想的DCG，IDCG的依据是：是根据rel(i)降序排列，即排列到最好状态。算出最好排列的DCG，就是IDCG。

IDCG=最好排列的DCG

对于上述的例子，按照rel(i)进行降序排列的最好状态为list_best=[B,D,A,C,E]

i	rel(i)	log(i+1)	rel(i)/log(i+1)
1 = B	0.9	1	0.9
2 = D	0.6	1.59	0.38
3 = A	0.5	2	0.25
4 = C	0.3	2.32	0.13
5 = E	0.1	2.59	0.04

IDCG = list_best的DCG_best = 0.9+0.38+0.25+0.13+0.04=1.7 (理所当然，IDCG>DCG_1和DCG_2)

因为不同query的搜索结果有多有少，所以不同query的DCG值就没有办法来做对比。所以提出NDCG。

所以NDGC使用DCG/IDCG来表示，这样的话，NDCG就是一个相对值，那么不同query之间就可以通过NDCG值进行比较评估。

参考文章

• NDCG
• 搜索评价指标——NDCG
• 推荐系统中的常用评价指标：NDCG，Recall，AUC，GAUC
• NDCG及实现

推荐系统评估指标

1. Hit Ratio(HR)

在top-K推荐中，HR是一种常用的衡量召回率的指标，其计算公式如下：

分母是所有的测试集合，分子式每个用户top-K推荐列表中属于测试集合的个数的总和。举个简单的例子，三个用户在测试集中的商品个数分别是10，12，8，模型得到的top-10推荐列表中，分别有6个，5个，4个在测试集中，那么此时HR的值是 (6+5+4)/(10+12+8) = 0.5。

2. Mean Average Precision(MAP)

在了解MAP(Mean Average Precision)之前，先来看一下AP(Average Precision), 即为平均准确率。

对于AP可以用这种方式理解: 假使当我们使用google搜索某个关键词，返回了10个结果。当然最好的情况是这10个结果都是我们想要的相关信息。但是假如只有部分是相关的，比如5个，那么这5个结果如果被显示的比较靠前也是一个相对不错的结果。但是如果这个5个相关信息从第6个返回结果才开始出现，那么这种情况便是比较差的。这便是AP所反映的指标，与recall的概念有些类似，不过是“顺序敏感的recall”。

比如对于用户 u, 我们给他推荐一些物品，那么 u 的平均准确率定义为：

用一个例子来解释AP的计算过程：

因此该user的AP为（1 + 0.66 + 0.5） ／ 3 = 0.72

那么对于MAP(Mean Average Precision)，就很容易知道即为所有用户 u 的AP再取均值(mean)而已。那么计算公式如下：

3. Mean Reciprocal Rank (MRR)

MRR计算公式如下：

其中|Q|是用户的个数，ranki是对于第i个用户，推荐列表中第一个在ground-truth结果中的item所在的排列位置。

举个例子，有三个用户，推荐列表中正例的最小rank值分别为3，2，1，那么MRR=(1 + 0.5 + 0.33) / 3 = 0.61

4. ILS

ILS是衡量推荐列表多样性的指标，计算公式如下：

如果S(bi,bj)计算的是i和j两个物品的相似性，如果推荐列表中物品越不相似，ILS越小，那么推荐结果的多样性越好。

参考文章

• 推荐系统遇上深度学习(十六)–详解推荐系统中的常用评测指标
• 如何量化评估推荐系统的推荐结果？
• 推荐系统研究中常用的评价指标
• 浅谈推荐系统的评估指标
• 在你做推荐系统的过程中都遇到过什么坑？

其它指标

介绍下Pearson相关系数

要理解Pearson相关系数，首先要理解协方差（Covariance），协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反，公式如下：

Pearson相关系数公式如下：

由公式可知，Pearson相关系数是用协方差除以两个变量的标准差得到的，虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但是协方差值的大小并不能很好地度量两个随机变量的关联程度，例如，现在二维空间中分布着一些数据，我们想知道数据点坐标X轴和Y轴的相关程度，如果X与Y的相关程度较小但是数据分布的比较离散，这样会导致求出的协方差值较大，用这个值来度量相关程度是不合理的，如下图：

为了更好的度量两个随机变量的相关程度，引入了Pearson相关系数，其在协方差的基础上除以了两个随机变量的标准差，容易得出，pearson是一个介于-1和1之间的值，当两个变量的线性关系增强时，相关系数趋于1或-1；当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；如果相关系数等于0，表明它们之间不存在线性相关关系。《数据挖掘导论》给出了一个很好的图来说明：

参考文章

• 如何理解皮尔逊相关系数（Pearson Correlation Coefficient）？