深入理解函数式编程（上）

函数式编程是一种历史悠久的编程范式。作为演算法，它的历史可以追溯到现代计算机诞生之前的λ演算，本文希望带大家快速了解函数式编程的历史、基础技术、重要特性和实践法则。在内容层面，主要使用JavaScript语言来描述函数式编程的特性，并以演算规则、语言特性、范式特性、副作用处理等方面作为切入点，通过大量演示示例来讲解这种编程范式。同时，文末列举比较一些此范式的优缺点，供读者参考。因为文章涵盖一些范畴论知识，可能需要其他参考资料一起辅助阅读。

前言

本文分为上下两篇，上篇讲述函数式编程的基础概念和特性，下篇讲述函数式编程的进阶概念、应用及优缺点。函数式编程既不是简单的堆砌函数，也不是语言范式的终极之道。我们将深入浅出地讨论它的特性，以期在日常工作中能在对应场景中进行灵活应用。

1. 先览：代码组合和复用

在前端代码中，我们现有一些可行的模块复用方式，比如：

除了上面提到的组件和功能级别的代码复用，我们也可以在软件架构层面上，通过选择一些合理的架构设计来减少重复开发的工作量，比如说很多公司在中后台场景中大量使用的低代码平台。

可以说，在大部分软件项目中，我们都要去探索代码组合和复用。

函数式编程，曾经有过一段黄金时代，后来又因面向对象范式的崛起而逐步变为小众范式。但是，函数式编程目前又开始在不同的语言中流行起来了，像Java 8、JS、Rust等语言都有对函数式编程的支持。

今天我们就来探讨JavaScript的函数，并进一步探讨JavaScript中的函数式编程（关于函数式编程风格软件的组织、组合和复用）。

2. 什么是函数式编程？

2.1 定义

函数式编程是一种风格范式，没有一个标准的教条式定义。我们来看一下维基百科的定义：

函数式编程是一种编程范式，它将电脑运算视为函数运算，并且避免使用程序状态以及易变对象。其中，λ演算是该语言最重要的基础。而且λ演算的函数可以接受函数作为输入的参数和输出的返回值。

我们可以直接读出以下信息：

1. 避免状态变更
2. 函数作为输入输出
3. 和λ演算有关

那什么是λ演算呢？

2.2 函数式编程起源：λ演算

λ演算（读作lambda演算）由数学家阿隆佐·邱奇在20世纪30年代首次发表，它从数理逻辑（Mathematical logic）中发展而来，使用变量绑定（binding）和代换规则（substitution）来研究函数如何抽象化定义（define）、函数如何被应用（apply）以及递归（recursion）的形式系统。

λ演算和图灵机等价（图灵完备，作为一种研究语言又很方便）。

通常用这个定义形式来表示一个λ演算。

所以λ演算式就三个要点：

1. 绑定关系。变量任意性，x、y和z都行，它仅仅是具体数据的代称。
2. 递归定义。λ项递归定义，M可以是一个λ项。
3. 替换归约。λ项可应用，空格分隔表示对M应用N，N可以是一个λ项。

比如这样的演算式：

通过变量代换（substitution）和归约（reduction），我们可以像化简方程一样处理我们的演算。

λ演算有很多方式进行，数学家们也总结了许多和它相关的规律和定律（可查看维基百科）。

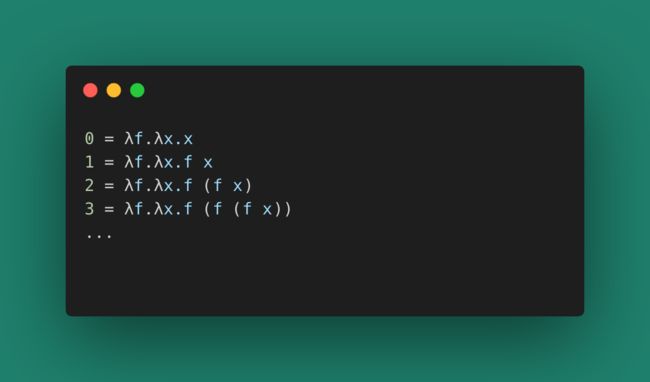
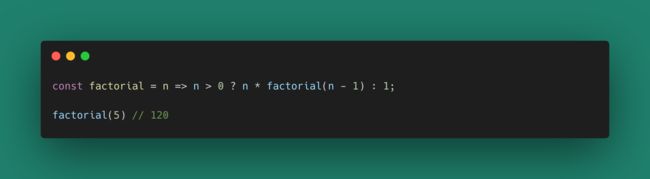
举个例子，小时候我们学习整数就是学会几个数字，然后用加法/减法来推演其他数字。在函数式编程中，我们可以用函数来定义自然数，有很多定义方式，这里我们讲一种实现方式：

上面的演算式表示有一个函数f和一个参数x。令0为x，1为f x，2为f f x…

什么意思呢？这是不是很像我们数学中的幂：a^x（a的x次幂表示a对自身乘x次）。相应的，我们理解上面的演算式就是数字n就是f对x作用的次数。有了这个数字的定义之后，我们就可以在这个基础上定义运算。

其中SUCC表示后继函数（+1操作），PLUS表示加法。现在我们来推导这个正确性。

这样，进行λ演算就像是方程的代换和化简，在一个已知前提（公理，比如0/1，加法）下，进行规则推演。

2.2.1 演算：变量的含义

在λ演算中我们的表达式只有一个参数，那它怎么实现两个数字的二元操作呢？比如加法a + b，需要两个参数。

这时，我们要把函数本身也视为值，可以通过把一个变量绑定到上下文，然后返回一个新的函数，来实现数据（或者说是状态）的保存和传递，被绑定的变量可以在需要实际使用的时候从上下文中引用到。

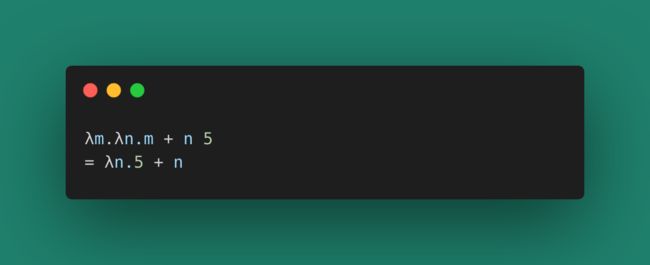
比如下面这个简单的演算式：

第一次函数调用传入m=5，返回一个新函数，这个新函数接收一个参数n，并返回m + n的结果。像这种情况产生的上下文，就是Closure（闭包，函数式编程常用的状态保存和引用手段），我们称变量m是被**绑定（binding）**到了第二个函数的上下文。

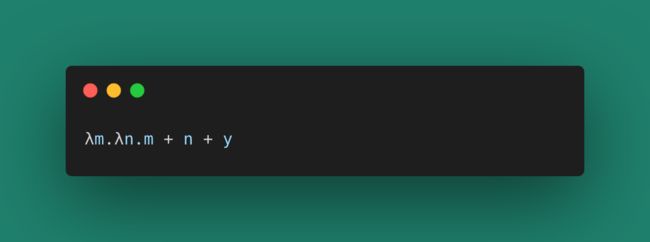
除了绑定的变量，λ演算也支持自由的变量，比如下面这个y：

这里的y是一个没有绑定到参数位置的变量，被称为一个自由变量。

绑定变量和自由变量是函数的两种状态来源，一个可以被代换，另一个不能。实际程序中，通常把绑定变量实现为局部变量或者参数，自由变量实现为全局变量或者环境变量。

2.2.2 演算：代换和归约

演算分为Alpha代换和Beta归约。 前面章节我们实际上已经涉及这两个概念，下面来介绍一下它们。

Alpha代换指的是变量的名称是不重要的，你可以写λm.λn.m + n，也可以写λx.λy.x + y，在演算过程中它们表示同一个函数。也就是说我们只关心计算的形式，而不关心细节用什么变量去实现。这方便我们不改变运算结果的前提下去修改变量命名，以方便在函数比较复杂的情况下进行化简操作。实际上，连整个lambda演算式的名字也是不重要的，我们只需要这种形式的计算，而不在乎这个形式的命名。

Beta归约指的是如果你有一个函数应用（函数调用），那么你可以对这个函数体中与标识符对应的部分做代换（substitution），方式为使用参数（可能是另一个演算式）去替换标识符。听起来有点绕口，但是它实际上就是函数调用的参数替换。比如：

可以使用1替换m，3替换n，那么整个表达式可以化简为4。这也是函数式编程里面的引用透明性的由来。需要注意的是，这里的1和3表示表达式运算值，可以替换为其他表达式。比如把1替换为(λm.λn.m + n 1 3)，这里就需要做两次归约来得到下面的最终结果：

2.3 JavaScript中的λ表达式：箭头函数

ECMAScript 2015规范引入了箭头函数，它没有this，没有arguments。只能作为一个表达式（expression）而不能作为一个声明式（statement），表达式产生一个箭头函数引用，该箭头函数引用仍然有name和length属性，分别表示箭头函数的名字、形参（parameters）长度。一个箭头函数就是一个单纯的运算式，箭头函数我们也可以称为lambda函数，它在书写形式上就像是一个λ演算式。

可以利用箭头函数做一些简单的运算，下例比较了四种箭头函数的使用方式：

这是直接针对数字（基本数据类型）的情况，如果是针对函数做运算（引用数据类型），事情就变得有趣起来了。我们看一下下面的示例：

fn_x类型，表明我们可以利用函数内的函数，当函数被当作数据传递的时候，就可以对函数进行应用（apply），生成更高阶的操作。 并且x => y => x(y)可以有两种理解，一种是x => y函数传入X => x(y)，另一种是x传入y => x(y)。

add_x类型表明，一个运算式可以有很多不同的路径来实现。

上面的add_1/add_2/add_3我们用到了JavaScript的立即运算表达式IIFE。

λ演算是一种抽象的数学表达方式，我们不关心真实的运算情况，我们只关心这种运算形式。因此上一节的演算可以用JavaScript来模拟。下面我们来实现λ演算的JavaScript表示。

我们把λ演算中的f和x分别取为countTime和x，代入运算就得到了我们的自然数。

这也说明了不管你使用符号系统还是JavaScript语言，你想要表达的自然数是等价的。这也侧面说明λ演算是一种形式上的抽象（和具体语言表述无关的抽象表达）。

2.4 函数式编程基础：函数的元、柯里化和Point-Free

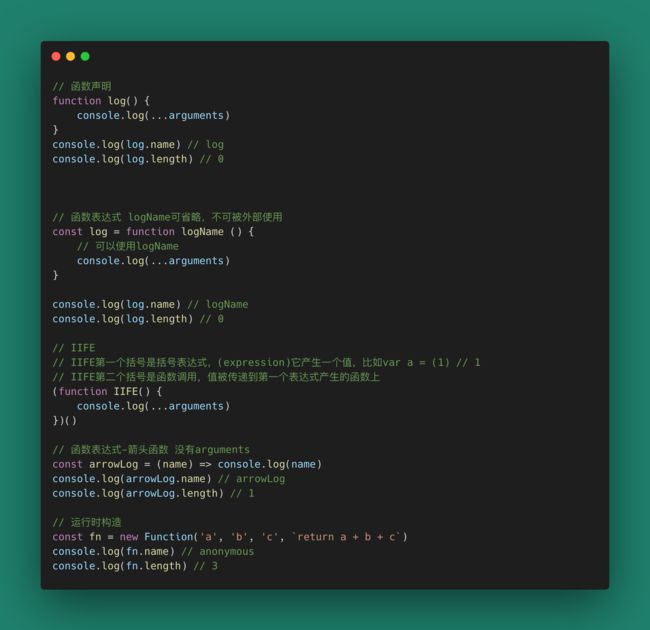
回到JavaScript本身，我们要探究函数本身能不能带给我们更多的东西？我们在JavaScript中有很多创建函数的方式：

虽然函数有这么多定义，但function关键字声明的函数带有arguments和this关键字，这让他们看起来更像是对象方法（method），而不是函数（function） 。

况且function定义的函数大多数还能被构造（比如new Array）。

接下来我们将只研究箭头函数，因为它更像是数学意义上的函数（仅执行计算过程）。

• 没有arguments和this。
• 不可以被构造new。

2.4.1 函数的元：完全调用和不完全调用

不论使用何种方式去构造一个函数，这个函数都有两个固定的信息可以获取：

• name 表示当前标识符指向的函数的名字。
• length 表示当前标识符指向的函数定义时的参数列表长度。

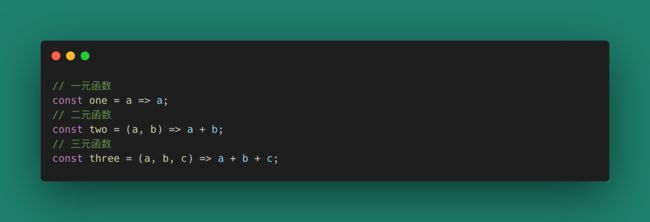
在数学上，我们定义f(x) = x是一个一元函数，而f(x, y) = x + y是一个二元函数。在JavaScript中我们可以使用函数定义时的length来定义它的元。

定义函数的元的意义在于，我们可以对函数进行归类，并且可以明确一个函数需要的确切参数个数。函数的元在编译期（类型检查、重载）和运行时（异常处理、动态生成代码）都有重要作用。

如果我给你一个二元函数，你就知道需要传递两个参数。比如+就可以看成是一个二元函数，它的左边接受一个参数，右边接受一个参数，返回它们的和（或字符串连接）。

在一些其他语言中，+确实也是由抽象类来定义实现的，比如Rust语言的trait Add。

但我们上面看到的λ演算，每个函数都只有一个元。为什么呢？

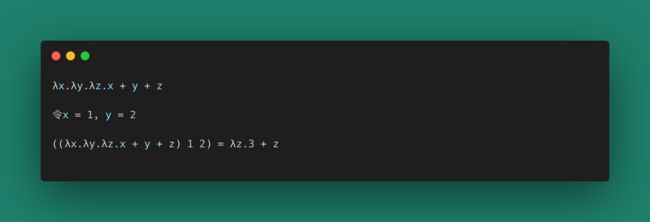
只有一个元的函数方便我们进行代数运算。λ演算的参数列表使用λx.λy.λz的格式进行分割，返回值一般都是函数，如果一个二元函数，调用时只使用了一个参数，则返回一个「不完全调用函数」。这里用三个例子解释“不完全调用”。

第一个，不完全调用，代换参数后产生了一个不完全调用函数 λz.3 + z。

第二个，Haskell代码，调用一个函数add（类型为a -> a -> a），得到另一个函数add 1（类型为a -> a）。

第三个，上一个例子的JavaScript版本。

“不完全调用”在JavaScript中也成立。实际上它就是JavaScript中闭包（Closure，上面我们已经提到过）产生的原因，一个函数还没有被销毁（调用没有完全结束），你可以在子环境内使用父环境的变量。

注意，上面我们使用到的是一元函数，如果使用三元函数来表示addThree，那么函数一次性就调用完毕了，不会产生不完全调用。

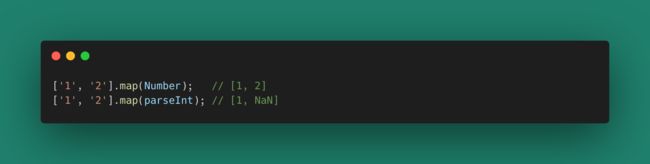
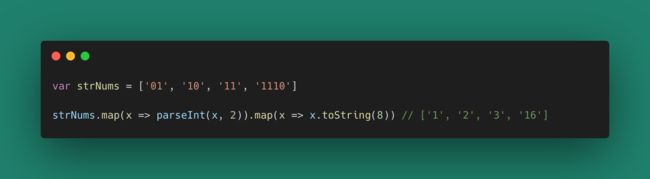
函数的元还有一个著名的例子（面试题）：

造成上述结果的原因就是，Number是一元的，接受map第一个参数就转换得到返回值；而parseInt是二元的，第二个参数拿到进制为1（map函数为三元函数，第二个参数返回元素索引），无法输出正确的转换，只能返回NaN。这个例子里面涉及到了一元、二元、三元函数，多一个元，函数体就多一个状态。如果世界上只有一元函数就好了！我们可以全通过一元函数和不完全调用来生成新的函数处理新的问题。

认识到函数是有元的，这是函数式编程的重要一步，多一个元就多一种复杂度。

2.4.2 柯里化函数：函数元降维技术

柯里化（curry）函数是一种把函数的元降维的技术，这个名词是为了纪念我们上文提到的数学家阿隆佐·邱奇。

首先，函数的几种写法是等价的（最终计算结果一致）。

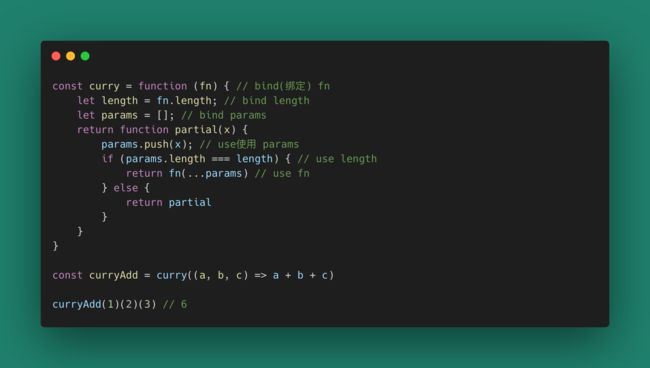
这里列一个简单的把普通函数变为柯里化函数的方式（柯里化函数Curry）。

柯里化函数帮助我们把一个多元函数变成一个不完全调用，利用Closure的魔法，把函数调用变成延迟的偏函数(不完全调用函数)调用。这在函数组合、复用等场景非常有用。比如：

虽然你可以用其他闭包方式来实现函数的延迟调用，但Curry函数绝对是其中形式最美的几种方式之一。

2.4.3 Point-Free｜无参风格：函数的高阶组合

函数式编程中有一种Point-Free风格，中文语境大概可以把point认为是参数点，对应λ演算中的函数应用（Function Apply），或者JavaScript中的函数调用（Function Call），所以可以理解Point-Free就指的是无参调用。

来看一个日常的例子，把二进制数据转换为八进制数据：

这段代码运行起来没有问题，但我们为了处理这个转换，需要了解 parseInt(x, 2) 和 toString(8) 这两个函数（为什么有魔法数字2和魔法数字8），并且要关心数据（函数类型a -> b）在每个节点的形态（关心数据的流向）。有没有一种方式，可以让我们只关心入参和出参，不关心数据流动过程呢？

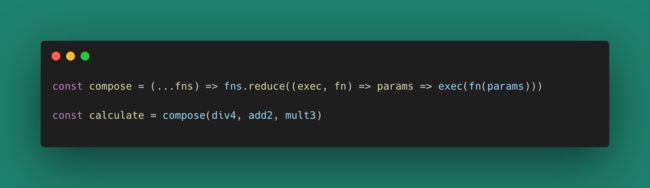
上面的方法假设我们已经有了一些基础函数toBinary（语义化，消除魔法数字2）和toStringOx（语义化，消除魔法数字8），并且有一种方式（pipe）把基础函数组合（Composition）起来。如果用Typescript表示我们的数据流动就是：

用Haskell表示更简洁，后面都用Haskell类型表示方式，作为我们的符号语言。

值得注意的是，这里的x-> [int] ->y我们不用关心，因为**pipe(…)**函数帮我们处理了它们。pipe就像一个盒子。

BOX内容不需要我们理解。而为了达成这个目的，我们需要做这些事：

• utils 一些特定的工具函数。
• curry 柯里化并使得函数可以被复用。
• composition 一个组合函数，像胶水一样粘合所有的操作。
• name 给每个函数定义一个见名知意的名字。

综上，Point-Free风格是粘合一些基础函数，最终让我们的数据操作不再关心中间态的方式。这是函数式编程，或者说函数式编程语言中我们会一直遇到的风格，表明我们的基础函数是值得信赖的，我们仅关心数据转换这种形式，而不是过程。JavaScript中有很多实现这种基础函数工具的库，最出名的是Lodash。

可以说函数式编程范式就是在不停地组合函数。

2.5 函数式编程特性

说了这么久，都是在讲函数，那么究竟什么是函数式编程呢？在网上你可以看到很多定义，但大都离不开这些特性。

• First Class 函数：函数可以被应用，也可以被当作数据。
• Pure 纯函数，无副作用：任意时刻以相同参数调用函数任意次数得到的结果都一样。
• Referential Transparency 引用透明：可以被表达式替代。
• Expression 基于表达式：表达式可以被计算，促进数据流动，状态声明就像是一个暂停，好像数据到这里就会停滞了一下。
• Immutable 不可变性：参数不可被修改、变量不可被修改—宁可牺牲性能，也要产生新的数据（Rust内存模型例外）。
• High Order Function 大量使用高阶函数：变量存储、闭包应用、函数高度可组合。
• Curry 柯里化：对函数进行降维，方便进行组合。
• Composition 函数组合：将多个单函数进行组合，像流水线一样工作。

另外还有一些特性，有的会提到，有的一笔带过，但实际也是一个特性（以Haskell为例）。

• Type Inference 类型推导：如果无法确定数据的类型，那函数怎么去组合？（常见，但非必需）
• Lazy Evaluation 惰性求值：函数天然就是一个执行环境，惰性求值是很自然的选择。
• Side Effect IO：一种类型，用于处理副作用。一个不能执行打印文字、修改文件等操作的程序，是没有意义的，总要有位置处理副作用。（边缘）

数学上，我们定义函数为集合A到集合B的映射。在函数式编程中，我们也是这么认为的。函数就是把数据从某种形态映射到另一种形态。注意理解“映射”，后面我们还会讲到。

2.5.1 First Class：函数也是一种数据

函数本身也是数据的一种，可以是参数，也可以是返回值。

通过这种方式，我们可以让函数作为一种可以保存状态的值进行流动，也可以充分利用不完全调用函数来进行函数组合。把函数作为数据，实际上就让我们有能力获取函数内部的状态，这样也产生了闭包。但函数式编程不强调状态，大部分情况下，我们的“状态”就是一个函数的元（我们从元获取外部状态）。

2.5.2 纯函数：无状态的世界

通常我们定义输入输出（IO）是不纯的，因为IO操作不仅操作了数据，还操作了这个数据范畴外部的世界，比如打印、播放声音、修改变量状态、网络请求等。这些操作并不是说对程序造成了破坏，相反，一个完整的程序一定是需要它们的，不然我们的所有计算都将毫无意义。

但纯函数是可预测的，引用透明的，我们希望代码中更多地出现纯函数式的代码，这样的代码可以被预测，可以被表达式替换，而更多地把IO操作放到一个统一的位置做处理。

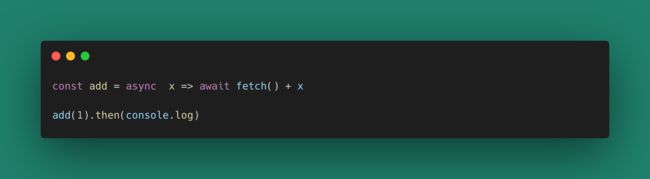
这个add函数是不纯的，但我们把副作用都放到它里面了。任意使用这个add函数的位置，都将变成不纯的（就像是async/await的传递性一样）。需要说明的是抛开实际应用来谈论函数的纯粹性是毫无意义的，我们的程序需要和终端、网络等设备进行交互，不然一个计算的运行结果将毫无意义。但对于函数的元来说，这种纯粹性就很有意义，比如：

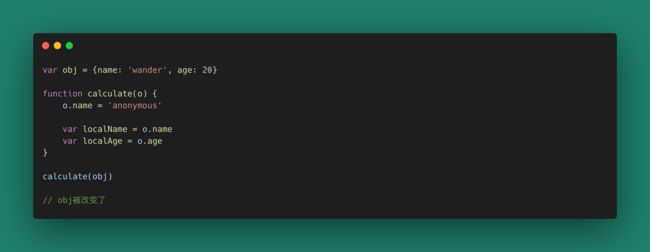
当函数的元像上面那样是一个引用值，如果一个函数的调用不去控制自己的纯粹性，对别人来说，可能会造成毁灭性打击。因此我们需要对引用值特别小心。

上面这种解构赋值的方式仅解决了第一层的引用值，很多其他情况下，我们要处理一个引用树、或者返回一个引用树，这需要更深层次的解引用操作。请小心对待你的引用。

函数的纯粹性要求我们时刻提醒自己降低状态数量，把变化留在函数外部。

2.5.3 引用透明：代换

通过表达式替代（也就是λ演算中讲的归约），可以得到最终数据形态。

也就是说，调用一个函数的位置，我们可以使用函数的调用结果来替代此函数调用，产生的结果不变。

一个引用透明的函数调用链永远是可以被合并式代换的。

2.5.4 不可变性：把简单留给自己

一个函数不应该去改变原有的引用值，避免对运算的其他部分造成影响。

一个充满变化的世界是混沌的，在函数式编程世界，我们需要强调参数和值的不可变性，甚至在很多时候我们可以为了不改变原来的引用值，牺牲性能以产生新的对象来进行运算。牺牲一部分性能来保证我们程序的每个部分都是可预测的，任意一个对象从创建到消失，它的值应该是固定的。

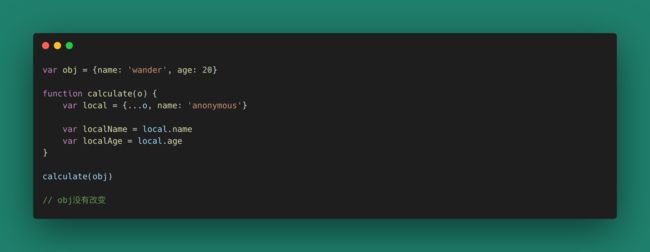
一个元如果是引用值，请使用一个副本（克隆、复制、替代等方式）来得到状态变更。

2.5.5 高阶：函数抽象和组合

JS中用的最多的就是Array相关的高阶函数。实际上Array是一种Monad（后面讲解）。

通过高阶函数传递和修改变量：

高阶函数实际上为我们提供了注入环境变量（或者说绑定环境变量）提供了更多可能。React的高阶组件就从这个思想上借用而来。一个高阶函数就是使用或者产生另一个函数的函数。高阶函数是函数组合（Composition）的一种方式。

高阶函数让我们可以更好地组合业务。常见的高阶函数有：

• map
• compose
• fold
• pipe
• curry
• …

2.5.6 惰性计算：降低运行时开销

惰性计算的含义就是在真正调用到的时候才执行，中间步骤不真实执行程序。这样可以让我们在运行时创建很多基础函数，但并不影响实际业务运行速度，唯有业务代码真实调用时才产生开销。

map(addOne)并不会真实执行+1，只有真实调用exec才执行。当然这个只是一个简单的例子，强大的惰性计算在函数式编程语言中还有很多其他例子。比如：

“无穷”只是一个字面定义，我们知道计算机是无法定义无穷的数据的，因此数据在take的时候才真实产生。

惰性计算让我们可以无限使用函数组合，在写这些函数组合的过程中并不产生调用。但这种形式，可能会有一个严重的问题，那就是产生一个非常长的调用栈，而虚拟机或者解释器的函数调用栈一般都是有上限的，比如2000个，超过这个限制，函数调用就会栈溢出。虽然函数调用栈过长会引起这个严重的问题，但这个问题其实不是函数式语言设计的逻辑问题，因为调用栈溢出的问题在任何设计不良的程序中都有可能出现，惰性计算只是利用了函数调用栈的特性，而不是一种缺陷。

记住，任何时候我们都可以重构代码，通过良好的设计来解决栈溢出的问题。

2.5.7 类型推导

当前的JS有TypeScript的加持，也可以算是有类型推导了。

没有类型推导的函数式编程，在使用的时候会很不方便，所有的工具函数都要查表查示例，开发中效率会比较低下，也容易造成错误。

但并不是说一门函数式语言必须要类型推导，这不是强制的。像Lisp就没有强制类型推导，JavaScript也没有强制的类型推导，这不影响他们的成功。只是说，有了类型推导，我们的编译器可以在编译器期间提前捕获错误，甚至在编译之前，写代码的时候就可以发现错误。类型推导是一些语言强调的优秀特性，它确实可以帮助我们提前发现更多的代码问题。像Rust、Haskell等。

2.5.8 其他

你现在也可以总结一些其他的风格或者定义。比如强调函数的组合、强调Point-Free的风格等等。

3. 小结

函数式有很多基础的特性，熟练地使用这些特性，并加以巧妙地组合，就形成了我们的“函数式编程范式”。这些基础特性让我们对待一个function，更多地看作函数，而不是一个方法。在许多场景下，使用这种范式进行编程，就像是在做数学推导（或者说是类型推导），它让我们像学习数学一样，把一个个复杂的问题简单化，再进行累加/累积，从而得到结果。

同时，函数式编程还有一块大的领域需要进入，即副作用处理。不处理副作用的程序是毫无意义的（仅在内存中进行计算），下篇我们将深入函数式编程的应用，为我们的工程应用发掘出更多的特性。

4. 作者简介

俊杰，美团到家研发平台/医药技术部前端工程师。

阅读美团技术团队更多技术文章合集

前端 | 算法 | 后端 | 数据 | 安全 | 运维 | iOS | Android | 测试

| 在公众号菜单栏对话框回复【2021年货】、【2020年货】、【2019年货】、【2018年货】、【2017年货】等关键词，可查看美团技术团队历年技术文章合集。

| 本文系美团技术团队出品，著作权归属美团。欢迎出于分享和交流等非商业目的转载或使用本文内容，敬请注明“内容转载自美团技术团队”。本文未经许可，不得进行商业性转载或者使用。任何商用行为，请发送邮件至[email protected]申请授权。