计算机LCG/PCG/MWC/XorShift等PRNG算法，以及V8中Math.random()、webkit中crypto等随机算法的实现

计算机LCG/PCG/MWC/XorShift等PRNG算法，以及V8中Math.random()、webkit中crypto等随机算法的实现

本文篇幅较长，如想直接看 js 的随机数实现可定位本文ECMAScript JavaScript实现章节。

*本人github：https://github.com/MichealWayne，本人博客地址：https://blog.michealwayne.cn/

引言

无论用哪种编程语言开发，都有很多场景有生成随机数的需求。当然在日常开发过程中，我们会直接调用API方法来实现，比如js的Math.random()、Python的random()，但其实现随机数的原理也是一个值得深究的问题。

随机数的应用场景

• 仿真：当使用一台计算机仿真自然现象时，就需要用随机数使事情变得更真，比如模拟机场人流。
• 抽样：通常要考察所有可能的情况是不实际的，而随机的抽样将使我们能了解“典型”的行为。
• 数值分析：利用随机数已经想出了许多巧妙的技术来解复杂的数值问题。
• 计算机程序设计：为验证计算机算法的有效性，随机值乃是数据的好来源。更重要的是，随机值对于随机化算法的运算是很要紧的，随机化算法经常比确定性算法要优越得多。
• 决策：许多决策人通过抛硬币或掷飞镖等来做出判断，做出这样完全“无偏见”的判断是重要的，随机性也是矩阵游戏理论中优化策略的必不可少的部分。
• 美学：一点儿随机性就会使计算机生成的图形和音乐似乎更活泼。
• 娱乐：摇骰子、洗扑克牌、转轮盘等娱乐方式，随意数的这些传统用法，已经被命名为“蒙特卡洛方法”，它已成为描述任何使用随机数的算法的通用术语。

也正因为有着如此多的应用，随机数的实现才显得格外重要。

随机数概念

概率论

首先来回顾下大学里概率论中与随机数相关的概念：

• 频率：定义在相同的条件下，进行了 n 次实验，在这 n 次实验中，事件 A 发生的次数 nA 称为事件 A 发生的频数，比值 nA/n 称为事件 A 发生的频率。
• 概率：设 E 是随机试验，S 是它的样本空间，对于 E 的每一事件 A 赋予一个实数，记为 P(A)，称为事件的概率。
• 随机变量：设随机试验的样本空间为 S={e}，若 X=X(e) 为定义在样本空间 S 上的实值单值函数，则称 X=X(e) 为随机变量。
• 随机事件：在条件 S 下可能发生也可能不发生的事件，叫相对于条件 S 的随机事件。

一个确定分布的独立的随机数序列：每个数的出现都只是偶然的，并且与这序列中的其他数无关，每个数入任何给定的范围都有一个确定的概率。

随机事件在一次试验中发生与否是随机的，但随机性中含有规律性。随机事件A的概率是频率的稳定值，频率是概率的近似值。

像 js 中的Math.random()在概率分布理论中属于连续和离散的均匀分布。均匀分布的特点是：所有基本事件的可能性相等。

判定标准

可以参考Federal Office for Information Security （德国联邦信息安全办公室）给出了随机数发生器质量评判的四个标准-BSI评估标准：

• K1 - 产生的随机数序列彼此不同的概率应该是很高的。
• K2 - 根据某些统计测试，无法分辨产生的序列和真随机序列。这些测试包括： monobit测试（序列中的0和1的数量相等）、poker测试（ chi-squared测试的特殊情况）、runs测试（不同长度运行的频率）、来自于BSI 和 NIST 的longruns测试、autocorrelation测试。
• K3 - 给定任何子序列，任何攻击者都无法计算后续序列或者生成器的内部状态。
• K4 - 给定生成器的内部状态，任何攻击者都无法计算之前的序列或者生成器之前的状态。
  对于密码学应用，只有满足K3和K4标准的生成器是可以接受的。。

计算机实现

确定性的方法无法真实地创造随机性，正如《计算机程序设计艺术（第二卷）》中所说：“当今使用的大部分随机数生成器都不够优秀，而且开发者倾向于拿来就用，不去了解具体的生成策略。以至于我们常常发现一些略有瑕疵、年代久远的随机数生成器会被盲目地用在一个又一个的程序中，而对于它们的局限性，却无人问津。”

发展历程

• 早期，那些在科学工作中需要随机数的人们，用一个“充分转动起来”的坛子中抓出球来或要骰子、分牌之类的办法获得随机数。

• 1927年，L.H.C.Tippett发布超过40000个随机数字的一张表，那些数字是“从人口统计调查报告中随机地取得的”。自那以后，已经造出了一些特殊的装置，用来机械地生成随机数。

• 1939年，M.G.Kendall和B.Babington-Smith使用头一部这样的机器造出了有100000个随机数字的一张表

• 1949年，D.H.Lehmer提出线性同余法（LCG）的算法方案。

• 1951年首次安装的Ferranti Mark Ⅰ计算机有一个内置指令，它使用一个电阻噪声生成器将20个随机位放入累加器中，这一功能受到了A.M.Turing的推荐。

• 1955年，RAND公司又公布了一张被广泛使用的有100万个随机数字的表，这张表是利用另一部特殊装置得到的。一台取名为ERNIE（厄尼）的著名随机数机器被使用了许多年，用于产生英国政府有奖债券的中奖号码。

• 在计算机问世之后不久，人们开始探求在计算机程序中求随机数的有效方法，可以使用一张表，但由于内存空间和输入时间的要求，这种方法的实用性有限。在20世纪90年代技术的发展又使这张表变得有用起来，因为CDROM上可以分布（存储）1GB的经过测试的随机数。

• 1995年，George Marsaglia 将一个噪声二极管的电流输出与确定的经过扰频的rap音乐叠加在一起生成了650MB的随机值（称之为黑白噪声）并把它们做成演示光盘，因而促进了随机数表的复兴。

• 2014年，计算机PRNG算法-PCG诞生，它以更小的，快速的代码和小的状态量实现了出色的统计性能。

算法（伪随机）

平方取中法-随机序列

早期用机械方式生成随机数的缺点，引起了人们利用一台计算机的普通算术操作来产生随机数的兴趣。1946年前后，Jogn von Neumann（冯诺伊曼）头一个建议利用这种方法。他的办法是取前面的随机数的平方，并抽取中部的数字。

例如，如果正在生成10位数字，并且先前的值是5772156649，则把它平方得到33317792380594909201，因此下一个数就是7923805949。

对于这种技术，有十分明显的异议：既然每个数完全由它先前的数所决定，那么以这样的方法产生的序列怎么会是随机的呢？这个序列当然不是随机的，仅仅像是随机的而已。在典型的应用中，一个数与跟在它后面的那个数之间的真实关系并无客观的意义，因此，这种非随机性的特征并不真是不可取的。从直观上看，平方取中似乎相当充分地搅乱了前面的数。

已经证明，冯诺伊曼的这种方法并不是求随机数的好方法，危险在于这个序列容易出现重复元素的短循环。例如，如果0一旦作为这个序列的一个数出现，则它将不断地重现本身。

一些人在20世纪50年代初曾以“平方取中法”进行了实验。G.E.Forsythe用4位数字代替10位数字，试验了16个不同的初始值，结果发现，其中的12个导致了以循环6100、2100、4100、8100、6100,…为结局的序列，而其中有两个退化成0。N.Metropolis对平方取中法进行了广泛的试验，试验中大多采用二进数系统，他证明了：用20位数字进行工作时，序列可能退化成13个不同的循环，其中最长的循环周期位142。

π（Pi）—随机序列

1965年，根据I.J.Matrix博士的说法，数学家把π的十进制展开当做是随机序列，而对于一个现代数值逻辑学家说来，它有极丰富的值得注意的模式。

例如，Matrix博士指出，在π的展开式中头一次重复的两位数字是26，而它的第二次出现是在一个奇妙的重复模式中间

在列出许多位数字或它们的其他性质之后，人们就会发现，如果正确地解释的话，π可以反映人类经历的整个历史。

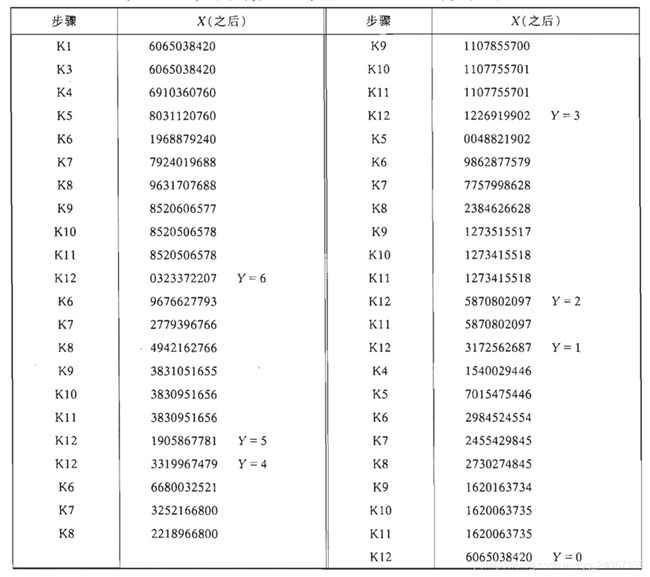
算法K-超随机数生成程序

（其中X是一个10位的十进制数）

考虑到算法 K 的复杂设计，这一算法似乎能产生无穷尽的令人难以置信的随机数，但事实上，当把这个算法头一次放到计算机上时，它几乎立即收敛到10位数值6065038420——非常巧合，本算法把这个数转换成它自己。若以另外一个数开始，则这个序列在7401个值之后，开始以长度为3178的周期进行循环

这个事告诉我们，随机数并不是通过随机地选择的方法就可生成的，应当使用某些理论。

PRNG

后文算法便是通过理论算法实现的，统称为 PRNG（pseudo random number generator）伪随机数生成器，又被称为确定性随机比特生成器（deterministic random bit generator，DRBG）。其中适合于加密应用程序的PRNG称为加密安全的 PRNG（CSPRNG）。CSPRNG 的一个必要条件是不知道初始种子的敌人在分辨生成器的输出序列和真随机序列时只有可忽略的优势。换句话说，若 PRNG 只需要通过特定统计测试时，则 CSPRNG 必须通过种子规模的多项式复杂度内的所有统计测试

PRNG 是一个生成数字序列的算法，其特性近似于随机数序列的特性。PRNG 生成的序列并不是真随机，因此它完全由一个初始值决定，这个初始值被称为 PRNG 的随机种子（seed，但这个种子可能包含真随机数）。尽管接近于真随机的序列可以通过硬件随机数生成器生成，但伪随机数生成器因为其生成速度和可再现的优势，在实践中也很重要。

PRNG 的周期定义为：所有初始值的最大长度的无重复前缀序列。周期受状态数的限制，通常用比特位数表示。然而，每增加一个比特位，周期长度就可能增加一倍，所以构建周期足够长的 PRNG 对于许多实际应用程序来说是很容易的。

线性同余法LCG（linear congruential generators）

当今使用的流行的随机数生成程序是 D.H.Lehmer 1949年介绍过的下列方案的特殊情况。我们选择 4 个魔术整数：

m, 模*数； 0

然后通过置公式（1）

Xn+1 = (aX0 + c) mod m,  n>=0

而得到所求的随机数序列。这个序列称做线性同余序列。对m求余有点像确定转动的轮盘上球的落点。

例如，当 m = 10 和 X0 = a = c = 7 时，得到的序列是：

7,6,9,0,7,6,9,0...

如此例所示，对于 m, a, c 和 X0 的所有选择，这个序列并不总是“随机”的。这个例子有一个长度为 4 的周期，也说明了同余序列总是进入一个循环的事实。

改进：

定义b = a - 1，a>=2, b>=1，公式（2）：

Xn+k = (a^k * Xn + (a^k - 1) * c / b) mod m,  k>=0, n>=0

它借助于第 n 项来直接表达第 (n + k) 项，由此得出，由的每第 k 项组成的子序列是另一个线性同余序列，该子序列具有乘数a^k mod m和增量((a^k - 1) * c / b) mod m。

这个公式的一个重要推论是：由m、a、c和X0定义的一般序列，能非常简单地借助c=1和X0=0的特殊情况来表示，设

Y0 = 0, Yn+1 = (a * Yn + 1) mod m

根据公式（2），我们得到Yk等于(a^k - 1) / b(modulo m)，因此公式（1）中定义的一般序列满足

Xn = (A * Yn + X0) mod m，其中A = (X0 * b + c) mod m

并且可以通过分析（详见《计算机程序设计艺术（第二卷）》3.2.1.1）得出m可以取2^31 - 1（2^32），乘数a选择在0.01m和0.99m之间，而且它的二进制表示或十进制表示数字不应有一个简单的正规模式，推荐值是（7^5，即16807）。

但是对于现代的计算机而言，这样的周期还是太短了。生成器的内部结构如栅栏结构和超平面点的分布也很重要。对于不同的生成器有特定的检测方法。结构检测用到最多的就是谱检验，谱检验就是基于相邻平行超平面之间最大距离的检验，该距离越大，生成器越差。

如图：

MWC-梅森旋转算法

1991年，MWC（multiply-with-carry）由 George Marsaglia 和 Zaman 发明，非常类似于 LCG。MWC以其最简单的形式使用与线性同余生成器类似的公式，但是c（“加数”）在每次迭代中都不同。

其优势在于调用简单的计算机整数算法，使得非常快速地生成具有巨大周期的随机数序列；生成的循环周期更长（2^60 ~ 2^2000000），接近于 CPU 的循环周期。

它被广泛运用于游戏类的开发中，被非正式地称为“所有PRNG的母亲”，这个名字最初由 Marsaglia 自己创造。

以下是使用128位乘法并具有64位输出的小型MWC生成器的c语言实现：

// C99 + __uint128_t MWC, 256 bits of state, period approx. 2^255

/* The state must be neither all zero, nor x = y = z = 2^64 - 1, c =
   MWC_A3 - 1. The condition 0 < c < MWC_A3 - 1 is thus sufficient. */
   
uint64_t x, y, z, c = 1;

#define MWC_A3 0xff377e26f82da74a

uint64_t inline next() {
    const __uint128_t t = MWC_A3 * (__uint128_t)x + c;
    x = y;
    y = z;
    c = t >> 64;
    return z = t;
}

MWC1616

一个高速、简便的 MWC 实现，其中 js 的 V8 引擎在早期就是用了它（见后文）。

#define ulong unsigned long

static ulong mwc1616_x = 1;
static ulong mwc1616_y = 2;

void seed_rand_mwc1616(ulong seed) {
    mwc1616_x = seed | 1;   /* Can't seed with 0 */
    mwc1616_y = seed | 2;
}

ulong rand_mwc1616(void) {
    mwc1616_x = 18000 * (mwc1616_x & 0xffff) + (mwc1616_x >> 16);
    mwc1616_y = 30903 * (mwc1616_y & 0xffff) + (mwc1616_y >> 16);
    return (mwc1616_x<<16)+(mwc1616_y&0xffff);
}

但是 MWC 无法通过 TestU01 的多项测试。

PCG

置换同余生成器（PCG, permuted congruential generator）是LCG的改进，2014产生。它以更小的，快速的代码和小的状态量实现了出色的统计性能。
PCG与传统线性同余生成器在以下三个方面有所不同：

• LCG模数和状态较大，通常是所需输出大小的两倍；
• 它使用2的幂模，这导致使用全周期发生器和无偏输出位特别有效的实现
• 状态不是直接输出，而是状态的最高有效位用于选择按位旋转或移位，将其应用于状态以产生输出。

也正是可变的旋转，消除了2次幂的LCG的低阶比特短时间周期的问题。

PCG系列包括许多变体。虽然实际建议仅使用64位和128位，但核心LCG的定义宽度为8位至128位。如PCG-XSH-RR：

#include 
static uint64_t       state      = 0x4d595df4d0f33173;		// Or something seed-dependent
static uint64_t const multiplier = 6364136223846793005u;
static uint64_t const increment  = 1442695040888963407u;	// Or an arbitrary odd constant

static uint32_t rotr32(uint32_t x, unsigned r)
{
	return x >> r | x << (-r & 31);
}

uint32_t pcg32(void)
{
	uint64_t x = state;
	unsigned count = (unsigned)(x >> 59);		// 59 = 64 - 5

	state = x * multiplier + increment;
	x ^= x >> 18;								// 18 = (64 - 27)/2
	return rotr32((uint32_t)(x >> 27), count);	// 27 = 32 - 5
}

void pcg32_init(uint64_t seed)
{
	state = seed + increment;
	(void)pcg32();
}

XorShift算法

XorShift随机数生成器，也称为移位寄存器生成器，是George Marsaglia发现的一类伪随机数生成器。它是线性反馈移位寄存器（LFSR）的子集，它们允许在软件中进行特别有效的实现，而无需使用过于稀疏的多项式。

它的实现基本原理是通过重复取其自身或移位版本的数字的异或来生成其序列中的下一个数字，这使得它具有高效的特征。

它的缺点也是众所周知的，可以通过将它们与非线性函数结合来加以修正，例如在xorshift+或xorshift*生成器中。

xorshift有三种简单的模式：32-bit、64-bit、128-bit，如下列c的实现：

#include 

/* 32-bit */
struct xorshift32_state {
  uint32_t a;
}
uint32_t xorshift32 (struct xorshiift32_state *state) {
  uint32_t x = state->a;
  x ^= x << 13;
  x ^= x >> 17;
  x ^= x << 5;
  return state->a=x;
}


/* 64-bit */
struct xorshift64_state {
  uint64_t a;
}
uint64_t xorshift64 (struct xorshift64_state *state) {
  uint64_t x = state->a;
  x ^= x << 13;
  x ^= x >> 7;
  x ^= x << 17;
  return state->a=x;
}

/* 128-bit */
struct xorshift128_state {
  uint32_t a, b, c, d;
}
uint32_t xorshift128(struct xorshift128_state *state) {
  uint32_t t = state->d;
  uint32_t const s = state->a;
  state->d = state->c;
  state->c = state->b;
  state->b = s;
  
  t ^= t << 11;
  t ^= t >> 8;
  return state->a = t ^ s ^ (s >> 19);
}

其中128位算法通过了顽固测试，但是它没有通过 TestU01 框架的 BigCrush 测试套件的 MatrixRank 和 LinearComp 测试。所有 xorshift 生成器(包括下面的优化)都无法通过其中的某些测试，但是很容易通过对这种发生器的输出进行干扰以提升其质量。

xsorrow

Marsaglia 建议通过将输出与简单的加法计数器模2^32（Weyl序列）组合，这会使周期增加2^32倍，达到2^192-2^32。

#include 
struct xorwow_state {
  uint32_t a, b, c, d, e;
  uint32_t counter;
}
uint32_t xorwow (struct xorwow_state *state) {
  uint32_t t = state->e;
  uint32_t s = state->a;
  state->e = state->d;
  state->d = state->c;
  state->c = state->b;
  state->b = s;
  t ^= t >> 2;
  t ^= t << 1;
  t ^= s ^ (s << 4);
  state->a = t;
  state->counter += 362437;
  return t + state->counter
}

该生成器的典型案例是 Nvidia CUDA 工具包。

xorshift*

xorshift* 采用 xorshift 生成器，并对其输出应用可逆乘法（以字大小为模），作为非线性变换。

以下具有64位状态的64位生成器的最大周期为2^64-1，仅TestU01 BigCrush 的 MatrixRank 测试失败：

#include 
struct xorshift64s_state {
  uint64_t a;
}
uint64_t xorshift64s (struct xorshift64s_state *state) {
  uint64_t x = state->a;
  x ^= x >> 12;
  x ^= x << 25;
  x ^= x >> 27;
  state->a = x;
  return x * UINT64_C(0x2545F4914F6CDD1D);
}

Vigna 建议使用下面的xorshift1024 *生成器，该生成器具有1024位状态且最大周期为2^1024-1：

#include 

/* The state must be seeded so that there is at least one non-zero element in array */
struct xorshift1024s_state {
	uint64_t array[16];
	int index;
};

uint64_t xorshift1024s(struct xorshift1024s_state *state)
{
	int index = state->index;
	uint64_t const s = state->array[index++];
	uint64_t t = state->array[index &= 15];
	t ^= t << 31;		// a
	t ^= t >> 11;		// b
	t ^= s ^ (s >> 30);	// c
	state->array[index] = t;
	state->index = index;
	return t * (uint64_t)1181783497276652981;
}

xorshift+

除了使用乘法，还可以使用加法作为更快的非线性变换。这个想法最初是由 Saito 和 Matsumoto（还负责Mersenne Twister）在 XSadd 生成器中提出的，该生成器基于32位移位将基础xorshift生成器的两个连续输出相加。

但是，其输出的低阶位有一些弱点；当输出字位反转时，它在几次 BigCrush 测试中失败。为了解决这个问题，Vigna 引入了基于64位移位的 xorshift + 系列：以下 xorshift128 + 生成器使用 128 位状态，最大周期为2^128-1。

#include 

struct xorshift128p_state {
  uint64_t a, b;
};

/* The state must be seeded so that it is not all zero */
uint64_t xorshift128p(struct xorshift128p_state *state)
{
	uint64_t t = state->a;
	uint64_t const s = state->b;
	state->a = s;
	t ^= t << 23;		// a
	t ^= t >> 17;		// b
	t ^= s ^ (s >> 26);	// c
	state->b = t;
	return t + s;
}

此生成器是通过 BigCrush 测试最快的生成器之一，添加连续输出的一个缺点是，底层的 xorshift128 生成器是二维分布的，而关联的 xorshift128 + 生成器只有一维分布的。

xorshift+没有通过BigCrush的反向测试。

xoshiro 和 xoroshiro

xoshiro 和 xoroshiro 是移位寄存器生成器的其他变体，除了移位之外还使用旋转。根据Vigna的说法，与 xorshift 相比，它们速度更快，并产生更好的质量输出。
此类生成器具有32位和64位整数和浮点输出的变体。对于浮点数，取高53位（对于binary64）或高23位（对于binary32），因为高位的质量比浮点生成器中的低位更好。该算法还包括跳转功能，该功能将状态向前设置若干步（通常为2的幂），以允许许多执行线程从不同的初始状态开始。

xoshiro256**是该系列的通用随机64位数字生成器：

/*  Adapted from the code included on Sebastian Vigna's website */

#include 

uint64_t rol64(uint64_t x, int k)
{
	return (x << k) | (x >> (64 - k));
}

struct xoshiro256ss_state {
	uint64_t s[4];
};

uint64_t xoshiro256ss(struct xoshiro256ss_state *state)
{
	uint64_t *s = state->s;
	uint64_t const result = rol64(s[1] * 5, 7) * 9;
	uint64_t const t = s[1] << 17;

	s[2] ^= s[0];
	s[3] ^= s[1];
	s[1] ^= s[2];
	s[0] ^= s[3];

	s[2] ^= t;
	s[3] = rol64(s[3], 45);

	return result;
}

xoshiro256+ 比 xoshiro256** 快约15％，但最低的三位具有较低的线性复杂度；因此，应仅通过提取高53位数值并将其用于浮点结果。

#include 

uint64_t rol64(uint64_t x, int k)
{
	return (x << k) | (x >> (64 - k));
}

struct xoshiro256p_state {
	uint64_t s[4];
};

uint64_t xoshiro256p(struct xoshiro256p_state *state)
{
	uint64_t (*s)[4] = &state->s;
	uint64_t const result = s[0] + s[3];
	uint64_t const t = s[1] << 17;

	s[2] ^= s[0];
	s[3] ^= s[1];
	s[1] ^= s[2];
	s[0] ^= s[3];

	s[2] ^= t;
	s[3] = rol64(s[3], 45);

	return result;
}

值得注意的是：如果空间有限，则xoroshiro128 **等同于xoshiro256 **，xoroshiro128 +等同于xoshiro256 +。它们具有较小的状态空间，因此对于大规模并行程序没有多大用处。 xoroshiro128 +还表现出对Hamming权重的轻微依赖，在输出5TB数据后会产生故障。
对于32位输出，xoshiro128 ** 和xoshiro128 +完全等同于xoshiro256 **和xoshiro256 +。

算法检验

原则上，在设计随机算法的时候，我们会希望初始状态使用尽可能少的内存，执行速度更快，循环周期更长，且随机性质量越高。

理论检验主要是检验随机数的周期，内在结构和关联性。不过光理论检验是不够的，我们还需要经验检验。经验检验性对较简单，且有很多的方法。比如：等分布检验：又称均匀性检验，将[0,1)区间分成k个相等的子区间，落在每个子区间的伪随机数个数应该相等。常用的是x^2检验。序列检验：相继的数偶独立一致分布。计算的是数偶对的出现次数。间隔检验：用来考察在某个范围内序列的出现的间隔长度。扑克检验：考虑5个相继整数组成的n个组，观察其出现模式…

随机性的质量测试主要可以通过工具TestU01，它是一个软件库，以ANSI C语言实现，并提供了用于对统一随机数生成器进行经验统计测试的实用程序的集合。
TestU01直接测试的必须是一个能生成[0,1)之间浮点数的函数或一个能生成32位全随机无符号整数的函数。
它的整套测试被称作BigCrush，是目前最严格的随机数测试套件，它可以很好地检测一个随机数生成器的可靠程度。

如下图所示，只有7中RNG算法通过了测试，详细测试报告可见：
https://www.pcg-random.org/pdf/toms-oneill-pcg-family-v1.02.pdf

*优秀的 PRNG 还有很多，像非常安全且周期极长的 Mersenne Twiste（马特赛特旋转演算法），本文暂时先不记录。

---

具体实现

1.ECMAScript（JavaScript）

js随机数的主要生成方式毫无疑问是通过Math.random()，首先我们来看官方文档（ES6）对这个方法的介绍：

简单翻译来说就是通过在0～1范围内以大致均匀的分布随机或伪随机生成一个0～1范围内的数字。以V8引擎为例，我们来看看Math.random()的具体实现：

直至v4.9.40版本，V8选择的是MWC1616算法，核心内容：

uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616 () {
  state0 = 18030 * (state0 & 0xFFFF) + (state0 >> 16);
  state1 = 30903 * (state1 & 0xFFFF) + (state1 >> 16);
  return state0 << 16 + (state1 & 0xFFFF);
}

MWC1616的计算速度很快，且占用很少的内存，但是它的质量低于标准水平：

• 1.范围限制：这种算法的随机数范围在2^32以内，但是双精度浮点数能代表2^52个0～1的小数；

• 2.结果控制：结果值的上半部分非常依赖于state0；如果初始状态选择不正确，周期长度可能少于4亿；

• 3.无法通过TestU01的多项测试。

因此V8对随机数的算法进行了优化（v4.9.41.0开始，Chrome49开始）：

最新（2021.04.11）V8的实现（目录地址：v8/src/numbers/）

首先来看Math.random()的源码（v8/src/numbers/math-random.cc）：

// Copyright 2018 the V8 project authors. All rights reserved.
// Use of this source code is governed by a BSD-style license that can be
// found in the LICENSE file.

#include "src/numbers/math-random.h"

#include "src/base/utils/random-number-generator.h"
#include "src/common/assert-scope.h"
#include "src/execution/isolate.h"
#include "src/objects/contexts-inl.h"
#include "src/objects/fixed-array.h"
#include "src/objects/smi.h"

namespace v8 {
namespace internal {

void MathRandom::InitializeContext(Isolate* isolate,
                                   Handle native_context) {
  Handle cache = Handle::cast(
      isolate->factory()->NewFixedDoubleArray(kCacheSize));
  for (int i = 0; i < kCacheSize; i++) cache->set(i, 0);
  native_context->set_math_random_cache(*cache);
  Handle> pod =
      PodArray::New(isolate, 1, AllocationType::kOld);
  native_context->set_math_random_state(*pod);
  ResetContext(*native_context);
}

void MathRandom::ResetContext(Context native_context) {
  native_context.set_math_random_index(Smi::zero());
  State state = {0, 0};
  PodArray::cast(native_context.math_random_state()).set(0, state);
}

Address MathRandom::RefillCache(Isolate* isolate, Address raw_native_context) {
  Context native_context = Context::cast(Object(raw_native_context));
  DisallowHeapAllocation no_gc;
  PodArray pod =
      PodArray::cast(native_context.math_random_state());
  State state = pod.get(0);
  // Initialize state if not yet initialized. If a fixed random seed was
  // requested, use it to reset our state the first time a script asks for
  // random numbers in this context. This ensures the script sees a consistent
  // sequence.
  if (state.s0 == 0 && state.s1 == 0) {
    uint64_t seed;
    if (FLAG_random_seed != 0) {
      seed = FLAG_random_seed;
    } else {
      isolate->random_number_generator()->NextBytes(&seed, sizeof(seed));
    }
    state.s0 = base::RandomNumberGenerator::MurmurHash3(seed);
    state.s1 = base::RandomNumberGenerator::MurmurHash3(~seed);
    CHECK(state.s0 != 0 || state.s1 != 0);
  }

  FixedDoubleArray cache =
      FixedDoubleArray::cast(native_context.math_random_cache());
  // Create random numbers.
  for (int i = 0; i < kCacheSize; i++) {
    // Generate random numbers using xorshift128+.
    base::RandomNumberGenerator::XorShift128(&state.s0, &state.s1);
    cache.set(i, base::RandomNumberGenerator::ToDouble(state.s0));
  }
  pod.set(0, state);

  Smi new_index = Smi::FromInt(kCacheSize);
  native_context.set_math_random_index(new_index);
  return new_index.ptr();
}

}  // namespace internal
}  // namespace v8

总的来说，此文件与随机数生成相关的主要内容：

• 生成和控制随机种子state.s0和state.s1（调用random-number-generator.h的方法：base::RandomNumberGenerator::MurmurHash3(seed)和base::RandomNumberGenerator::MurmurHash3(~seed)）

  • *其中seed来源于v8/src/base/utils/random-number-generator.cc ：

    int64_t seed = Time::NowFromSystemTime().ToInternalValue() << 24;
      seed ^= TimeTicks::HighResolutionNow().ToInternalValue() << 16;
      seed ^= TimeTicks::Now().ToInternalValue() << 8;
      SetSeed(seed);
    

    即根据时间信息进行位运算处理，所以seed也是一个伪随机数。

• 调用random-number-generator.h的方法：base::RandomNumberGenerator::XorShift128(&state.s0, &state.s1);

• 设置和控制seed缓存

所以核心生成还是在v8/src/base/utils/random-number-generator.cc文件中：

// Copyright 2013 the V8 project authors. All rights reserved.
// Use of this source code is governed by a BSD-style license that can be
// found in the LICENSE file.

#include "src/base/utils/random-number-generator.h"

#include 
#include 

#include 
#include 

#include "src/base/bits.h"
#include "src/base/macros.h"
#include "src/base/platform/mutex.h"
#include "src/base/platform/time.h"
#include "src/base/platform/wrappers.h"

namespace v8 {
namespace base {

static LazyMutex entropy_mutex = LAZY_MUTEX_INITIALIZER;
static RandomNumberGenerator::EntropySource entropy_source = nullptr;

// static
void RandomNumberGenerator::SetEntropySource(EntropySource source) {
  MutexGuard lock_guard(entropy_mutex.Pointer());
  entropy_source = source;
}


RandomNumberGenerator::RandomNumberGenerator() {
  // Check if embedder supplied an entropy source.
  {
    MutexGuard lock_guard(entropy_mutex.Pointer());
    if (entropy_source != nullptr) {
      int64_t seed;
      if (entropy_source(reinterpret_cast(&seed),
                         sizeof(seed))) {
        SetSeed(seed);
        return;
      }
    }
  }

#if V8_OS_CYGWIN || V8_OS_WIN
  // Use rand_s() to gather entropy on Windows. See:
  // https://code.google.com/p/v8/issues/detail?id=2905
  unsigned first_half, second_half;
  errno_t result = rand_s(&first_half);
  DCHECK_EQ(0, result);
  result = rand_s(&second_half);
  DCHECK_EQ(0, result);
  SetSeed((static_cast(first_half) << 32) + second_half);
#elif V8_OS_MACOSX || V8_OS_FREEBSD || V8_OS_OPENBSD
  // Despite its prefix suggests it is not RC4 algorithm anymore.
  // It always succeeds while having decent performance and
  // no file descriptor involved.
  int64_t seed;
  arc4random_buf(&seed, sizeof(seed));
  SetSeed(seed);
#else
  // Gather entropy from /dev/urandom if available.
  FILE* fp = base::Fopen("/dev/urandom", "rb");
  if (fp != nullptr) {
    int64_t seed;
    size_t n = fread(&seed, sizeof(seed), 1, fp);
    base::Fclose(fp);
    if (n == 1) {
      SetSeed(seed);
      return;
    }
  }

  // We cannot assume that random() or rand() were seeded
  // properly, so instead of relying on random() or rand(),
  // we just seed our PRNG using timing data as fallback.
  // This is weak entropy, but it's sufficient, because
  // it is the responsibility of the embedder to install
  // an entropy source using v8::V8::SetEntropySource(),
  // which provides reasonable entropy, see:
  // https://code.google.com/p/v8/issues/detail?id=2905
  int64_t seed = Time::NowFromSystemTime().ToInternalValue() << 24;
  seed ^= TimeTicks::HighResolutionNow().ToInternalValue() << 16;
  seed ^= TimeTicks::Now().ToInternalValue() << 8;
  SetSeed(seed);
#endif  // V8_OS_CYGWIN || V8_OS_WIN
}


int RandomNumberGenerator::NextInt(int max) {
  DCHECK_LT(0, max);

  // Fast path if max is a power of 2.
  if (bits::IsPowerOfTwo(max)) {
    return static_cast((max * static_cast(Next(31))) >> 31);
  }

  while (true) {
    int rnd = Next(31);
    int val = rnd % max;
    if (std::numeric_limits::max() - (rnd - val) >= (max - 1)) {
      return val;
    }
  }
}


double RandomNumberGenerator::NextDouble() {
  XorShift128(&state0_, &state1_);
  return ToDouble(state0_);
}


int64_t RandomNumberGenerator::NextInt64() {
  XorShift128(&state0_, &state1_);
  return bit_cast(state0_ + state1_);
}


void RandomNumberGenerator::NextBytes(void* buffer, size_t buflen) {
  for (size_t n = 0; n < buflen; ++n) {
    static_cast(buffer)[n] = static_cast(Next(8));
  }
}

static std::vector ComplementSample(
    const std::unordered_set& set, uint64_t max) {
  std::vector result;
  result.reserve(max - set.size());
  for (uint64_t i = 0; i < max; i++) {
    if (!set.count(i)) {
      result.push_back(i);
    }
  }
  return result;
}

std::vector RandomNumberGenerator::NextSample(uint64_t max,
                                                        size_t n) {
  CHECK_LE(n, max);

  if (n == 0) {
    return std::vector();
  }

  // Choose to select or exclude, whatever needs fewer generator calls.
  size_t smaller_part = static_cast(
      std::min(max - static_cast(n), static_cast(n)));
  std::unordered_set selected;

  size_t counter = 0;
  while (selected.size() != smaller_part && counter / 3 < smaller_part) {
    uint64_t x = static_cast(NextDouble() * max);
    CHECK_LT(x, max);

    selected.insert(x);
    counter++;
  }

  if (selected.size() == smaller_part) {
    if (smaller_part != n) {
      return ComplementSample(selected, max);
    }
    return std::vector(selected.begin(), selected.end());
  }

  // Failed to select numbers in smaller_part * 3 steps, try different approach.
  return NextSampleSlow(max, n, selected);
}

std::vector RandomNumberGenerator::NextSampleSlow(
    uint64_t max, size_t n, const std::unordered_set& excluded) {
  CHECK_GE(max - excluded.size(), n);

  std::vector result;
  result.reserve(max - excluded.size());

  for (uint64_t i = 0; i < max; i++) {
    if (!excluded.count(i)) {
      result.push_back(i);
    }
  }

  // Decrease result vector until it contains values to select or exclude,
  // whatever needs fewer generator calls.
  size_t larger_part = static_cast(
      std::max(max - static_cast(n), static_cast(n)));

  // Excluded set may cause that initial result is already smaller than
  // larget_part.
  while (result.size() != larger_part && result.size() > n) {
    size_t x = static_cast(NextDouble() * result.size());
    CHECK_LT(x, result.size());

    std::swap(result[x], result.back());
    result.pop_back();
  }

  if (result.size() != n) {
    return ComplementSample(
        std::unordered_set(result.begin(), result.end()), max);
  }
  return result;
}

int RandomNumberGenerator::Next(int bits) {
  DCHECK_LT(0, bits);
  DCHECK_GE(32, bits);
  XorShift128(&state0_, &state1_);
  return static_cast((state0_ + state1_) >> (64 - bits));
}


void RandomNumberGenerator::SetSeed(int64_t seed) {
  initial_seed_ = seed;
  state0_ = MurmurHash3(bit_cast(seed));
  state1_ = MurmurHash3(~state0_);
  CHECK(state0_ != 0 || state1_ != 0);
}


uint64_t RandomNumberGenerator::MurmurHash3(uint64_t h) {
  h ^= h >> 33;
  h *= uint64_t{0xFF51AFD7ED558CCD};
  h ^= h >> 33;
  h *= uint64_t{0xC4CEB9FE1A85EC53};
  h ^= h >> 33;
  return h;
}

}  // namespace base
}  // namespace v8

可以看出核心是XorShift128+ 算法：

static inline void XorShift128(uint64_t* state0, uint64_t* state1) {
    uint64_t s1 = *state0;
    uint64_t s0 = *state1;
    *state0 = s0;
    s1 ^= s1 << 23;
    s1 ^= s1 >> 17;
    s1 ^= s0;
    s1 ^= s0 >> 26;
    *state1 = s1;
}

它使用128位内部状态，周期长度为2^128 - 1，并且 XorShift128+ 通过了TestU01的所有测试。

不过更新之后仍然会存在“密码学安全伪随机数生成”的危险，并且对于诸如散列、签名生成和加解密之类的用例，普通的PRNG不合适。因此便有了下面的模块。

crypto

为了解决上述问题，浏览器和node提供了解决方案：

1.浏览器环境（webkit）：安全变量API——crypto，window.crypto.getRandomValues

兼容情况：总体兼容较好

• 移动：iOS8起步，Android5起步
• PC：IE11，Chrome37起步

2.nodejs环境：加密模块-crypto，crypto.randomFill

兼容情况：此方法或替代方法在v4.x的文档中也能看到，所以几乎没有兼容问题。

这两种方式的使用方式本文不做介绍，它们为了确保足够的性能，不使用真正的随机数生成器，而是使用具有足够高质量的熵值作为伪随机数生成器的种子，如操作系统熵源（如"/dev/urandom"）。

它们都是牺牲性能成本返回加密安全随机值的方法，像uuid就用到了它们。

基于webkit的浏览器（Chrome、Safari）似乎使用基于ARC4的RNG，该RNG丢弃早期的密钥流，并每隔1.5mb混合系统OS熵。

webkit加密模块代码（/Source/WebCore/page/Crypto.cpp）：

/*
 * Copyright (C) 2011 Google Inc. All rights reserved.
 * Copyright (C) 2013 Apple Inc. All rights reserved.
 *
 * Redistribution and use in source and binary forms, with or without
 * modification, are permitted provided that the following conditions
 * are met:
 *
 * 1.  Redistributions of source code must retain the above copyright
 *     notice, this list of conditions and the following disclaimer. 
 * 2.  Redistributions in binary form must reproduce the above copyright
 *     notice, this list of conditions and the following disclaimer in the
 *     documentation and/or other materials provided with the distribution. 
 * 3.  Neither the name of Google, Inc. ("Google") nor the names of
 *     its contributors may be used to endorse or promote products derived
 *     from this software without specific prior written permission. 
 *
 * THIS SOFTWARE IS PROVIDED BY GOOGLE AND ITS CONTRIBUTORS "AS IS" AND ANY
 * EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED
 * WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
 * DISCLAIMED. IN NO EVENT SHALL APPLE OR ITS CONTRIBUTORS BE LIABLE FOR ANY
 * DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES
 * (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES;
 * LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND
 * ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT
 * (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF
 * THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
 */


#include "config.h"
#include "Crypto.h"

#include "Document.h"
#include "SubtleCrypto.h"
#include 
#include 

#if OS(DARWIN)
#include 
#include 
#endif

namespace WebCore {

Crypto::Crypto(ScriptExecutionContext* context)
    : ContextDestructionObserver(context)
#if ENABLE(WEB_CRYPTO)
    , m_subtle(SubtleCrypto::create(context))
#endif
{
}

Crypto::~Crypto() = default;

ExceptionOr Crypto::getRandomValues(ArrayBufferView& array)
{
    if (!isInt(array.getType()))
        return Exception { TypeMismatchError };
    if (array.byteLength() > 65536)
        return Exception { QuotaExceededError };
#if OS(DARWIN)
    auto rc = CCRandomGenerateBytes(array.baseAddress(), array.byteLength());
    RELEASE_ASSERT(rc == kCCSuccess);
#else
    cryptographicallyRandomValues(array.baseAddress(), array.byteLength());
#endif
    return { };
}

#if ENABLE(WEB_CRYPTO)

SubtleCrypto& Crypto::subtle()
{
    return m_subtle;
}

#endif

}

可以看出核心是调用了wtf/CryptographicallyRandomNumber.h的cryptographicallyRandomValues方法。

加密实现可见Source/WTF/wtf/CryptographicallyRandomNumber.cpp：

/*
 * Copyright (c) 1996, David Mazieres 
 * Copyright (c) 2008, Damien Miller 
 *
 * Permission to use, copy, modify, and distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR
 * ANY SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF
 * OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

/*
 * Arc4 random number generator for OpenBSD.
 *
 * This code is derived from section 17.1 of Applied Cryptography,
 * second edition, which describes a stream cipher allegedly
 * compatible with RSA Labs "RC4" cipher (the actual description of
 * which is a trade secret).  The same algorithm is used as a stream
 * cipher called "arcfour" in Tatu Ylonen's ssh package.
 *
 * RC4 is a registered trademark of RSA Laboratories.
 */

#include "config.h"
#include 

#include 
#include 
#include 
#include 

namespace WTF {

namespace {

class ARC4Stream {
    WTF_MAKE_FAST_ALLOCATED;
public:
    ARC4Stream();

    uint8_t i;
    uint8_t j;
    uint8_t s[256];
};

class ARC4RandomNumberGenerator {
    WTF_MAKE_FAST_ALLOCATED;
public:
    ARC4RandomNumberGenerator();

    uint32_t randomNumber();
    void randomValues(void* buffer, size_t length);

private:
    inline void addRandomData(unsigned char *data, int length);
    void stir();
    void stirIfNeeded();
    inline uint8_t getByte();
    inline uint32_t getWord();

    ARC4Stream m_stream;
    int m_count;
    Lock m_mutex;
};

ARC4Stream::ARC4Stream()
{
    for (int n = 0; n < 256; n++)
        s[n] = n;
    i = 0;
    j = 0;
}

ARC4RandomNumberGenerator::ARC4RandomNumberGenerator()
    : m_count(0)
{
}

void ARC4RandomNumberGenerator::addRandomData(unsigned char* data, int length)
{
    m_stream.i--;
    for (int n = 0; n < 256; n++) {
        m_stream.i++;
        uint8_t si = m_stream.s[m_stream.i];
        m_stream.j += si + data[n % length];
        m_stream.s[m_stream.i] = m_stream.s[m_stream.j];
        m_stream.s[m_stream.j] = si;
    }
    m_stream.j = m_stream.i;
}

void ARC4RandomNumberGenerator::stir()
{
    unsigned char randomness[128];
    size_t length = sizeof(randomness);
    cryptographicallyRandomValuesFromOS(randomness, length);
    addRandomData(randomness, length);

    // Discard early keystream, as per recommendations in:
    // http://www.wisdom.weizmann.ac.il/~itsik/RC4/Papers/Rc4_ksa.ps
    for (int i = 0; i < 256; i++)
        getByte();
    m_count = 1600000;
}

void ARC4RandomNumberGenerator::stirIfNeeded()
{
    if (m_count <= 0)
        stir();
}

uint8_t ARC4RandomNumberGenerator::getByte()
{
    m_stream.i++;
    uint8_t si = m_stream.s[m_stream.i];
    m_stream.j += si;
    uint8_t sj = m_stream.s[m_stream.j];
    m_stream.s[m_stream.i] = sj;
    m_stream.s[m_stream.j] = si;
    return (m_stream.s[(si + sj) & 0xff]);
}

uint32_t ARC4RandomNumberGenerator::getWord()
{
    uint32_t val;
    val = getByte() << 24;
    val |= getByte() << 16;
    val |= getByte() << 8;
    val |= getByte();
    return val;
}

uint32_t ARC4RandomNumberGenerator::randomNumber()
{
    auto locker = holdLock(m_mutex);

    m_count -= 4;
    stirIfNeeded();
    return getWord();
}

void ARC4RandomNumberGenerator::randomValues(void* buffer, size_t length)
{
    auto locker = holdLock(m_mutex);

    unsigned char* result = reinterpret_cast(buffer);
    stirIfNeeded();
    while (length--) {
        m_count--;
        stirIfNeeded();
        result[length] = getByte();
    }
}

ARC4RandomNumberGenerator& sharedRandomNumberGenerator()
{
    static LazyNeverDestroyed randomNumberGenerator;
    static std::once_flag onceFlag;
    std::call_once(
        onceFlag,
        [] {
            randomNumberGenerator.construct();
        });

    return randomNumberGenerator;
}

}

uint32_t cryptographicallyRandomNumber()
{
    return sharedRandomNumberGenerator().randomNumber();
}

void cryptographicallyRandomValues(void* buffer, size_t length)
{
    sharedRandomNumberGenerator().randomValues(buffer, length);
}

}

相比Math.random()，可以看出crypto的实现更为复杂，且有os依赖。

笔者也发现了webkit中如WebRtc单独实现了随机算法，其复杂度介于crypto和Math.random()之间，有兴趣可以去看一看/Source/webrtc/rtc_base/helpers.cc文件

后续我们随性用js写几个前文PRNG的js实现（虽然几乎毫无实际意义）：

简易实现随机数

方法1：MWC1616

const Utils = {
  state0: 1,
  state1: 2,
  getRandom: () => {
    let state0 = Utils.state0;
    let state1 = Utils.state1;
    Utils.state0 = state0 = 18030 * (state0 & 0xffff) + (state0 >> 16);
    Utils.state1 = state1 = 30903 * (state1 & 0xffff) + (state1 >> 16);
    return state0 << 16 + (state1 & 0xffff);
  }
};

// use:
// Utils.getRandom();

方法2：XorShift

• npm-xorshift

const Utils = {
    t: undefined,
    x: 123456789, 
    y: 362436069, 
    z: 521288629,
    getRandom () {
        let x = Utils.x;
        x ^= x << 16;
        x ^= x >> 5;
        x ^= x << 1;
    
        Utils.t = x;
        Utils.x = Utils.y;
        Utils.y = Utils.z;
        Utils.z = Utils.t ^ Utils.x ^ Utils.y;
        return Utils.z;
    }
}

方法3: XorShift128+

• https://www.npmjs.com/package/xorshift128plus

const Utils = {
  state0: 1,
  state1: 2,
  getRandom () {
    let s1 = Utils.state0;
    let s0 = Utils.state1;
    Utils.state0 = s0;
    s1 ^= s1 << 23;
    s1 ^= s1 >> 17;
    s1 ^= s0;
    s1 ^= s0 >> 26;
    Utils.state1 = s1;
    return Utils.state0 + Utils.state1;
  }
}

最后

本文的篇幅较长，总结一下主要内容：

• 1.随机数/随机序列的介绍、作用、定义；
• 2.一些常见的随机算法及检测工具介绍；
• 3.V8引擎的算法改进
• 4.随机算法的js实现

最后引入一句名言：

Any one who considers arithmetical methods of producing random digits is , of course, in a state of sin. ——JOHN VON NEUMANN, 1951

---

文篇博客地址：http://blog.michealwayne.cn/2021/04/11/notes/%E9%9A%8F%E6%9C%BA%E6%95%B0%E4%B8%8E%E8%AE%A1%E7%AE%97%E6%9C%BA%E5%AE%9E%E7%8E%B0/
有建议或转载可 -> [email protected]

---

相关链接

• http://www.math.sci.hiroshima-u.ac.jp/m-mat/MT/emt.html
• https://link.zhihu.com/?target=https%3A//www.bsi.bund.de/cae/servlet/contentblob/478152/publicationFile/30552/ais20e_pdf.pdf
• https://www.cnblogs.com/houkai/p/3807041.html
• https://www.w3cplus.com/javascript/tifu-by-using-math-random.html
• http://v8project.blogspot.tw/2015/12/theres-mathrandom-and-then-theres.html
• http://simul.iro.umontreal.ca/testu01/tu01.html
• http://simul.iro.umontreal.ca/testu01/guideshorttestu01.pdf
• https://www.javamex.com/tutorials/random_numbers/multiply_with_carry.shtml
• https://en.wikipedia.org/wiki/Multiply-with-carry_pseudorandom_number_generator
• http://www.helsbreth.org/random/rng_mwc1616.html
• https://en.wikipedia.org/wiki/Xorshift
• 《计算机程序设计艺术（第二卷）》
• https://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E5%8F%8D%E9%A6%88%E7%A7%BB%E4%BD%8D%E5%AF%84%E5%AD%98%E5%99%A8
• https://en.wikipedia.org/wiki/Multiply-with-carry
• https://github.com/v8/v8/tree/master/src
• https://zh.wikipedia.org/wiki/%E6%A6%82%E7%8E%87%E5%88%86%E5%B8%83
• http://www.voidcn.com/article/p-ddubmgpj-bbw.html
• https://developer.mozilla.org/en-US/docs/Web/API/Window/crypto
• https://zh.wikipedia.org/wiki/%E4%BC%AA%E9%9A%8F%E6%9C%BA%E6%95%B0%E7%94%9F%E6%88%90%E5%99%A8
• https://www.pcg-random.org/pdf/toms-oneill-pcg-family-v1.02.pdf
• https://cloud.tencent.com/developer/article/1836767