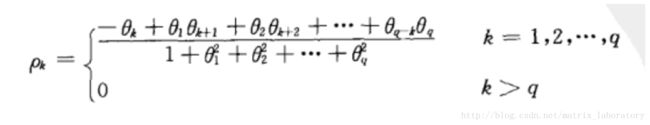金融时间序列分析：7. MA滑动平均模型

0. 目录

金融时间序列分析：9. ARMA自回归移动平均模型
金融时间序列分析：8. MA模型实例（Python）
金融时间序列分析：7. MA滑动平均模型
金融时间序列分析：6. AR模型实例
金融时间序列分析：5. AR模型实例（Python）
金融时间序列分析：4. AR自回归模型
金融时间序列分析：3. First Demo By Python
金融时间序列分析：2. 数学分析模型
金融时间序列分析：1. 基础知识

---

1. 前言

AR和MA模型是时序数据分析两个最基本的模型。

AR仅通过时间序列变量的自身历史观测值来反映有关因素对预测目标的影响和作用，不受模型变量相互独立的假设条件约束，所构成的模型可以消除普通回归预测方法中由于自变量选择、多重共线性等造成的困难

简单来说：AR模型是通过分析研究历史数据对当前数据的影响进行建模。

MA模型是用过去各个时期的随机干扰或预测误差的线性组合来表达当前预测值。

2. MA模型

q阶模型公式：

xt=μ+at−θ1at−1−...−θqat−q...........2.1

或者：

xt=μ+(1−θ1B−...−θqBq)at.............2.2

q⊆N+，μ为常量

3. MA（1）

3.1 模型公式

xt=μ+at−θat−1........................3.1

3.2 数学特征

期望

E(xt)=μ,.............3.2

推导方法：直接对公式3.1两边求期望即可

方差

Var(xt)=（1+θ2）σa2,....................3.3

推导方法：直接对公式3.1两边求方差即可

自协方差
为了简单，令 μ=0

在计算方差，协方差，相关系数时，对序列整体加减一常量不会对这几种数学特征的结果产生影响。

一阶

γ1=Cov(rt,rt−1)=−θσa2,..............3.4

k阶

γk=Cov(rt,rt−1)=0,k>0,..................3.5

所以对于MA（1）来说， xt只和xt−1 相关

自相关函数 ACF

ρk=⎧⎩⎨⎪⎪1,−θ1+θ2,0,if k=0if k=0if k>1

3.3 预测

从ACF可以看出，对于一阶MA模型来说，不会记忆1个周期以前的数据，所以只能进行单步预测；
超出一步预测后，数据将会变为均值

（1）预测

x̂ n(1)=μ−θan

（2）误差

en(1)=xn+1−x̂ n(1)=an+1

（3）误差波动率

Var(en(1))=σa2

4. MA（q）

4.1 模型公式

q阶模型公式：

xt=μ+at−θ1at−1−...−θqat−q...........4.1

或者：

xt=μ+(1−θ1B−...−θqBq)at.............4.2

q⊆N+，μ为常量

4.2 数学特征

期望

E(xt)=μ,.............4.3

方差

Var(xt)=（1+θ12+θ22+.....θq2）σa2,..........4.4

自相关函数 ACF

4.3 预测

和MA（1）模型一样。

超出q阶的多不预测数据收敛于均值。

5. 模型参数估计

首先用PACF对模型进行定阶，然后根据历史数据估算参数。
比如说我们通过PACF定阶，确认MA模型为3阶，那么就可以用
xt 的历史数据 xt−1,xt−2,xt−3 估算响应的参数，其中 at 就可以很简单的算出来。
其它参数的估计有两种方法：

6. 参考文献

[1] MIT， Analysis of Financial Time Series
[2] 金融时间序列分析, Ruey S. Tray
[3] 金融时间序列分析, 炼数成金