MOCO----Momentum Contrast
对比学习
这个博客写的很好,去看他的吧
对比学习是一种在高维(即指图片)的连续的输入信号上去构建字典的一种方式,这个字典是动态,因为这个字典里的key都是随机去取样的,而且用来给这些key做编码的也是在训练过程中不停地改变的。
如果要想学一个好的特征,这个字典必须有两个特性:1.字典要够大,因为大的字典能够包含很多语义丰富的负样本从而有助于学到那些更有判别性的特征,2.一致性:是为了模型的训练,能避免他学到一些trivial solution,就是一些捷径解。基于这些研究动机提出来momentum contrast
为什么要用queue来表示字典呢?
主要是受限于显卡的内存,把字典的大小和每次forward的batchSize大小剥离开。就是队列可以很大,队列可以很大,但是每次更新这个队列的时候是一点一点进行的;当我们用一个很小的batchSize的时候,现在这个batch抽得的特征进入队列,然后把最老的那个mini-batch移除队列,这样就把训练时用的Mini-batch的大小和队列的大小分开了。所以最后的队列的大小或字典的大小可以设置的非常大,因为它里面大部分的元素都不是每个iteration都需要更新的
如果只有一小部分,也就是说当前的batch是从当前的编码器得到的,而之前的key都是用不同时刻的编码器去抽取的特征,那就会产生编码不一致,可能是因为1个batch后会对编码器进行更新
改进:Momentum encoder
θ k θ_{k} θk 刚开始是由 θ q θ_{q} θq 初始化得来的,但是在模型训练的过程中,如果我们选择了一个很大的动量,那这个动量编码器 θ k θ_{k} θk 其实是更新的 非常缓慢的,它不会跟着这个 θ q θ_{q} θq 去快速的改变,从而保证这个字典里的所有的 k k k 都是由相似的编码器抽取得到的,尽最大可能的保持了他们之间的一致性,即编码器不能更新的太快,因为更新的太快的话,编码出来的相邻的 batch 之间的结果就很不一样。有点像模板变化太大不,那做出来的东西也不一样的,评判标准怎么定?
所以 MoCo 这个方法可以构建一个又大又一致的字典从而去无监督地学习视觉表征

设置 m=0.99

这一整个队列就是一个字典,里面的元素就是我们放进去的那些key,在模型训练的过程中,每一个mini-batch就会有新的一批key被送进来,同时也会有一批老的key移出去。所以作者说用队列的好处就是可以让我们重复用那些已经编码好的key,而这些key是从之前的mini-batch得到的。比如上图中的从左往右数的第2个batch里的key就是之前已经编码好送进来的,这样使用了字典后就可以把字典的大小和mini-batch的大小解耦,那我们在模型训练的过程中就可以使用一个标准的 mini-batchSize,一般就是128,256,而字典的大小就可以非常大,字典的大小非常灵活,字典的大小也可以当做一个超参数来单独设置,这个字典一直都是所有数据的一个子集,因为之前说到,想算对比学习的这个目标函数只是取一个近似,而不是在整个数据集上去算一个loss,而且使用队列这个数据结构可以让维护这个字典的计算开销非常小,字典的大小从几百到上万,整体的训练时间实际上是不变的,而且队列有先进先出的特性,这样每次移除队列的都是那些最老的batch,这样对于对比学习来说是很有利的,因为从一致性的角度来说,最早计算的那些batch的key是最早过时的,也就是说和最新算的batch的key是最不一致的。
因为队列太大了,所以无法给队列中的所有元素进行梯度回传,即key的编码器无法通过反向传播的方式去更新他的参数,那怎么办呢?总不能query编码器那边的那个fq一直在更新吧,但是你这边key的编码器就一直不动?作者提出了一个简单的方法,就是在每个iteration结束后,把更新好的编码器参数fq直接复制过来给这个key的编码器fk就行了,但是这样的效果并不好,作者认为可能是因为一个快速改变的编码器降低了这个队列里所有key的这个特征的一致性
假设batch=1,则k1,k2,k3,k4,k5这些key都是由不同的编码器产生的,那这样一个快速改变的编码器就会降低所有key之间的一致性,所以提出了一个动量更新的方式来解决这个问题

− l o g e x p ( Z x ) ∑ i = 1 K e x p ( Z i ) -log\frac{exp(Z_{x})}{\overset{K}{\underset{i=1}{\sum}} exp(Z_{i})} −logi=1∑Kexp(Zi)exp(Zx)
上面为softmax loss,也就是交叉熵损失函数
但是这在对比学习中并不适用,因为对比学习中Queue中的每个单独的个体就是一个类,K会变得非常大,类别太多,无法计算softmax和 loss func.
所以就产生了NCE Loss, noise contrastive estimation
NCE
NCE是将Queue中的数据简化为两个类别:data sample, noise sample, 每次只拿数据样本和噪声样本做对比即可,就是说可以把Queue中所有的负样本都当做noise sample, 而Queue中唯一的正样本当做data sample, 那实际上noise constractive解决了类别多的问题,但是计算复杂度没有降下来。
所以可以取近似,与其在整个数据集上计算loss, 不如从这个数据集中选取一些负样本来计算loss即可,这也就是estimation的含义,它只是一个估计,一种近似。
要求: 选取的样本不能太少,不然的话会没有那么近似。所以选取的样本要比较大,这样采样才更贴合实际。这也就是MoCo希望字典能够足够大的原因,因为越大的字典就能提供一个越好的近似
NCE就是把一些超级多类的分类问题,变成一系列的二分类问题,从而还可以使用softmax
InfoNCE:
是NCE一个简单的变体,即如果只把问题看做一个二分类,就只有data sample和noise sample的话可能对模型的学习不那么友好,也就是说负样本里面很有可能是正样本,所以还是把它看做一个多分类问题比较合理
L q = − log exp ( q ⋅ k + τ ) ∑ i = 0 K exp ( q ⋅ k i / τ ) \mathcal{L}_{q}=-\log \frac{\exp \left(\frac{q \cdot k_{+} }{\tau}\right)}{\sum_{i=0}^{K} \exp \left(q \cdot k_{i} / \tau\right)} Lq=−log∑i=0Kexp(q⋅ki/τ)exp(τq⋅k+)
其中: q q q 和 k k k都是模型出来的 l o g i t logit logit
τ \tau τ 是一个温度的超参数,一般用来控制分布的形状,比如说:原来的 logit分布大概如Fig1所示:
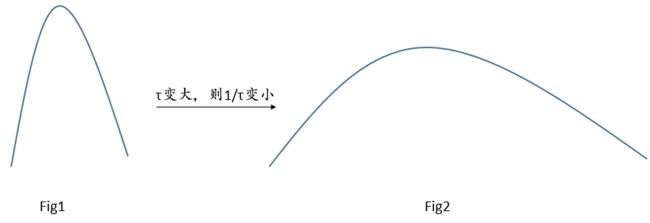
这样, τ \tau τ 变大的话,也就是 1 τ \frac{1}{\tau} τ1 变小了,相当于把这个分布里的数值都变小了,加上exp后就变得更小了,最后就会使分布变得更平滑,如Fig2所示。
τ \tau τ 变小的话,也就是 1 τ \frac{1}{\tau} τ1 变大了,相当于把这个分布里的数值都变大了,加上exp后就变得更大了,最后就会使分布变得更集中,也就是更peak, 更瘦,即Fig1所示。
如果温度设的越大,那对比损失对所有的负样本都一视同仁,导致模型的学习没有轻重;如果温度的值设的过小,又会让模型只关注那些特别特别困难的样本,而那些负样本很有可能是潜在的正样本,如果过渡关注特别困难的负样本,会导致模型很难收敛或者学好的特征不容易泛化。
其实温度这个超参数就是一个标量,如果忽略不看的话,InfoNCE其实就是cross entropy,做的就是一个K+1类的分类任务。(因为K个负样本,1个正样本)
