多元线性回归中的岭回归,LASSO和弹性网
这篇文字大致会写一写用多元线性回归一般会出现的情况。
通常如果说构造一个多元线性回归: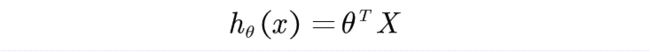
然后引入正态分布通过极大似然函数求解:
两边取对数后展开即得: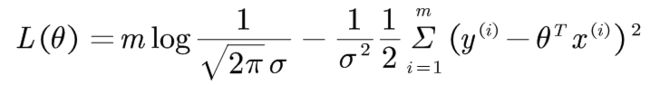
对该似然函数求最大值,恰好是求残差最小值。此时目标函数即为
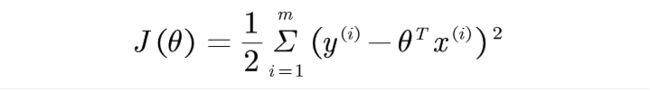
那么对其求偏导,最终为
将θ移至一边有: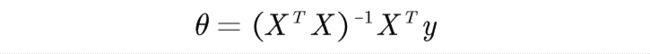
好了,此时有一个问题:XT X可逆否?
(1)如果可逆,那么直接解出来就有最优解。
(2)如果不可逆,下面给出几种解决方案
让我们先做一个问题转化:求该矩阵可逆等价于求该矩阵满秩,接下来,我们来看看什么情况矩阵才不能满秩。我们先假设X有n个样本,k个属性,那么XTX的秩就为k阶方阵,由线性方程组同解,我们可以知道r(XTX)=r(X),所以说求XTX满秩相当于求X满秩(r(X)=k)。
第一种情况,我们知道当属性的种类小于样本数时候即n 第二种情况,当出现完成多重共线性(即任意个属性完全相关,如当我知道其中一个属性的值,另一个随之得出)的情况,举个例子,比如我想要研究性别对薪资待遇的影响,我设了一个X1(男性为1,女性为0),X2(女性为1,男性为0),这就不得了了,当我们把这两个属性当成列向量塞进我们的大X的矩阵里,我们会发现这两列相关了,因为列向量线性相关所以该矩阵行列式为0,该矩阵退化不可逆。两种情况都说完了(小编在此只讨论了两种情况,并不绝对)。下面来探讨如何解决该问题。 来个切分数据集,我们发现GNP的那一列才是我们预测的目标 结果为: 与岭回归一样,LASSO也是擅长处理多重共线性问题,他同样也构造了惩罚项,但是LASSO的解释性很强,原因在于: 结果为: 弹性网这个概念是05年提出来的,比较新,结合了岭回归和弹性网,但是就别说这个结合了两者他就无敌了。下面看具体怎么样。给出他的损失函数 输出结果为: 这里小编弄了好久,legend加不上(分别在ax1和ax2和ax3下面plt.legend()会报错!),大家会的可以私信我,谢谢!!
(i)使用岭回归或者,让XT X可逆。(或者说LASSO和弹性网)
(ii)如果出现n
下面来说是岭回归如何让矩阵变成可逆,即上面最后一个公式,在我们的可逆矩阵里动手脚。岭回归
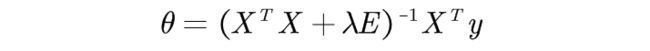
即我们在矩阵里加入了一个数量矩阵,该矩阵定是可逆的,如此,顺应地就达成我们的目标了。这里的λ是岭回归系数!下面让我们来看看,这个等式如何推导
也就是说,更改我们的损失函数就恰当的使用了岭回归。导包侠来试一番,数据集如下,选取了一个共线性较强的数据,大家很容易也看得出来。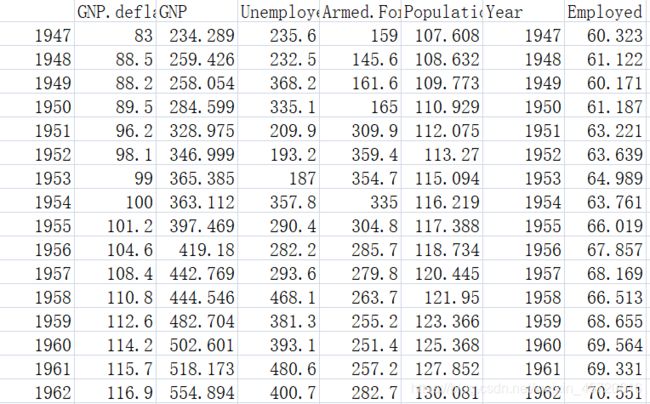
首先到了最喜欢的导包环节import pandas as pd
line_train=pd.read_csv('D:/BaiduNetdiskDownload/longley(1).csv')
from sklearn import linear_model
import matplotlib.pyplot as plt
import numpy as np
x_data=line_train.iloc[:,2:8]
y_data=line_train.iloc[:,1]
alpha__=np.linspace(0.001,1,100)#这里我们自己用自己切割的lamda
model_1=linear_model.RidgeCV(alpha__,store_cv_values=True)#后面这个参数=True指五折交叉检验
model_1.fit(x_data,y_data)
##画出lamda更新过程
plt.plot(alpha__,model.cv_values_.mean(axis=0))
plt.plot(model_1.alpha_,min(model_1.cv_values_.mean(axis=0)),'ro')
print('岭回归系数:',model_1.alpha_)#岭回归系数
y_predict_1=model_1.predict(x_data)
loss_1=sum((y_predict_1-y_data)**2)+sum(model_1.alpha_*abs(model_1.coef_))
print('岭回归损失值:',loss_1)
print("线性模型的参数为 w :",model_1.coef_)
print("线性模型的参数为 b:", model_1.intercept_)
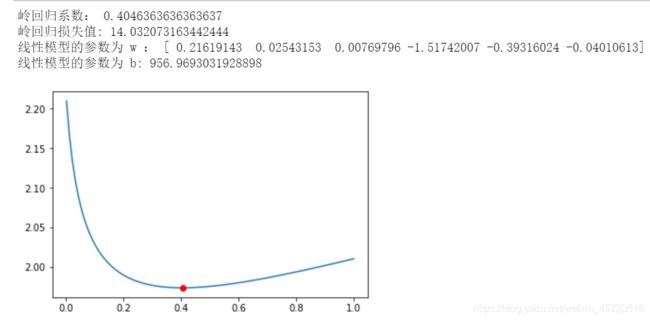
输出如下,这里输出了损失值,待会我们用这个数据集跟LASSO和弹性网比较。LASSO
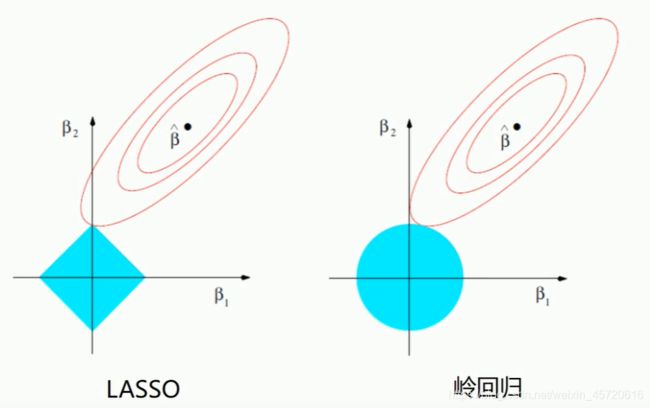 如果我们就两种属性分析,红色圆圈值每一个损失值的等高线。所以LASS更倾向于取顶点,如果扩大区域,虽然可以取其他蓝色趋于的点,但是损失值增大,而岭回归他就在β1和β2琢磨不定,这两个系数都很小的概率等于0,大多情况下是只能趋于0.这就给我们的模型的解释增大了难度。下面来看看LASSO是怎么样的。与岭回归相同,他也是增加了一个惩罚项,不过大家从上图也可以看出,他长什么样,岭回归是β1平方+β1平方对应的是圆。那么LASSO的损失函数为:
如果我们就两种属性分析,红色圆圈值每一个损失值的等高线。所以LASS更倾向于取顶点,如果扩大区域,虽然可以取其他蓝色趋于的点,但是损失值增大,而岭回归他就在β1和β2琢磨不定,这两个系数都很小的概率等于0,大多情况下是只能趋于0.这就给我们的模型的解释增大了难度。下面来看看LASSO是怎么样的。与岭回归相同,他也是增加了一个惩罚项,不过大家从上图也可以看出,他长什么样,岭回归是β1平方+β1平方对应的是圆。那么LASSO的损失函数为:

绝对值,所以说我们我们θ区域是个正方形。跟刚刚一样,这里就不给大家求了,大家可以按上面的推导,再对这个类似的进行操作。下面就来sklearn。这里的数据集接着上面的,而且x_data与y_data相同model_2=linear_model.LassoCV()
model_2.fit(x_data,y_data)
print('岭回归lamda:',model_2.alpha_)
print('岭回归回归系数:',model_2.coef_)
y_predict_2=model_2.predict(x_data)
print('岭回归预测值',y_predict_2)
loss_2=sum((y_predict_2-y_data)**2)+sum(model_2.alpha_*abs(model_2.coef_))
print("岭回归损失值",loss_2)

大家关注一下损失值。在这个数据集中暂且认为岭回归比LASSO好一点。弹性网ElasticNet
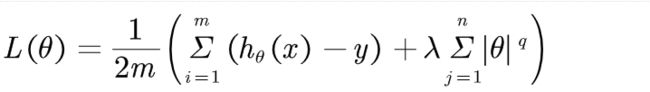
可以很明显的发现,这个人把两个东西搞到一起了。我们来看看不同的q值未知数的解空间
我们普遍取q=0.2,据大佬们多次考证,这个值损失的比较少。
那就来看看它怎么样model_3=linear_model.ElasticNetCV()
model_3.fit(x_data,y_data)
print('弹性lamda:',model_3.alpha_)
print('弹性网回归系数:',model_3.coef_)
y_predict_3=model_3.predict(x_data)
a=0.5
loss_3_1=sum((y_predict_3-y_data)**2)
loss_3_2=model_3.alpha_*(a*sum(model_3.coef_**2)+(1-a)*sum(abs(model_3.coef_)))
loss_3=loss_3_1+loss_3_2
print('弹性网误差为:',loss_3)

也不知道是操作错误还是咋地了,这个和LASSO同解啊,太奇妙了,但是这个损失函数就没那么辛运了,他比LASSO还大一点。
我们来比较一下这三个Year=line_train.iloc[:,0]
fig=plt.figure(figsize=(18,4))
s1=ax1=fig.add_subplot(1,3,1)
s2=ax2=fig.add_subplot(1,3,2)
ax3=fig.add_subplot(1,3,3)
ax1.plot(Year,y_predict_1,c='b',label='Ridge')
ax1.scatter(Year,y_data,c='r')
ax2.plot(Year,y_predict_2,c='y',label='LASSO')
ax2.scatter(Year,y_data,c='r')
ax3.plot(Year,y_predict_3,c='g',label='Elastic')
ax3.scatter(Year,y_data,c='r')
plt.legend()
plt.show()
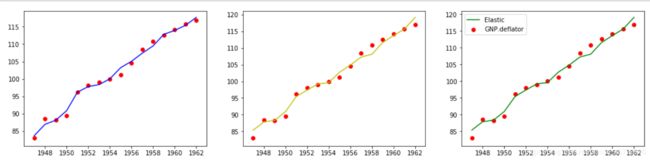
第一个是Ridge就是岭回归,第二个是LASSO,第三个是弹性网。其中2与3同解,所以画出来的预测值曲线一样。