如何理解线性回归的多重共线性、岭回归和Lasso（案例：波士顿房价数据集）

前言：本文主要介绍多重共线性、岭回归和Lasso的概念、公式推导及sklearn应用，使用的数据集为波士顿房价数据集、加利福尼亚房价数据集。

目录

如何从行列式理解多重共线性？

如何理解使用岭回归解决多重共线性？

如何在sklearn中使用linear_model.Ridge岭回归？（案例：波士顿房价数据集）

如何使用岭迹图选择最佳正则化参数？（案例：希尔伯特矩阵）

如何在sklearn中使用linear_model.RidgeCV，带交叉验证的岭回归？（案例：波士顿房价数据集）

如何理解Lasso，以及用Lasso进行特征选择？（案例：加利福尼亚房价数据集）

如何在sklearn中使用linear_model.LassoCV，带交叉验证的Lasso？（案例：加利福尼亚房价数据集）

---

如何从行列式理解多重共线性？

之前提及使用最小二乘法求解多元线性回归的损失函数，公式推导中需要左乘，但是没有讨论是否存在。

，为行列式，作为分母，那么等式成立的条件自然是不能等于0。

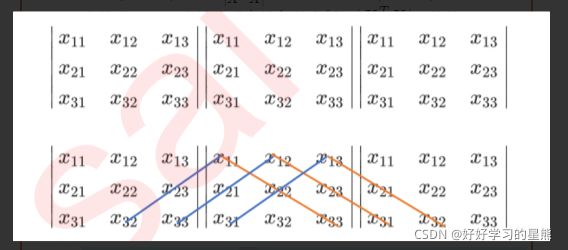
如何计算矩阵的行列式？

3条↘对角线元素相乘，然后相加，依次减去3条↙对角线元素相乘。

任何矩阵都有行列式，行列式通过初等行/列变换后大小不变，所以可以将行列式转换成梯形行列式，从而直接计算对角线元素之积即可求得行列式。

---

行列式不为0的条件为：当行列式通过变幻，变为对角矩阵时，对角线上的元素不为0。这种满足行列式变换后对角线元素不为0的矩阵，称为“满秩矩阵”。

可以通过numpy计算矩阵是否满秩

np.trace(array) # 计算矩阵对角线元素之和
np.linalg.det(array) # 计算矩阵的行列式，为0说明不满秩

如果，分母出现“除0错误”，称为特征存在精确相关关系；如果趋近于0，趋近于，称为特征存在高度相关关系。以上两种情况下，w都无法计算得出结果，统称为存在多重共线性。 

多重共线性属于相关性的一种，当特征存在高度相关、精确相关时，则称特征存在多重共线性。

---

多重共线性的解决方案有如下思路：

1. 使用统计学的先验思路，对特征进行相关性检验或降维；计算量增加；
2. 使用前向逐步回归法，筛选对模型高度相关的特征；计算量增大；
3. 对线性回归进行改进，使用岭回归、Lasso、弹性网等方式改进。

---

如何理解使用岭回归解决多重共线性？

岭回归解决多重共线性的办法为：在多元线性回归的损失函数上加上正则项：w的L2范式乘以正则化系数α，公式为：

岭回归解决多重共线性的原理：通过对对角线加上一个α，使变成满秩矩阵，从而消除多重共线性。其公式推导情况如下：

？没懂的地方：为什么上面是Xw-y，下面是y-Xw？

（中间左边变换，是因为令求导为0）

---

因为α可以人为设置，所以永远满秩，则不为0，所以存在，可以同时左乘，从而求解w。 

---

既然α可以人为设置，那么应该如何设置才能取得比较好的结果呢？首先，不能为0，否则永无效；其次不能太小，否则趋近于0，会产生高度精确相关，同样无法有效求解；并且也不能将α设置得太大，超过特征对模型的影响。

---

如何在sklearn中使用linear_model.Ridge岭回归？（案例：波士顿房价数据集）

为了选择合适的α，可以使用绘制学习曲线的方式，得出不同α对模型的影响。以下案例通过选取不同的正则化系数α，观察模型和MSE下不同的线性回归模型结果，数据集为波士顿房价数据集。

---

# 系数说明
Ridge(alpha=1.0 # 设定正则化系数
      , fit_intercept=True # 是否有截距项
      , normalize=False # 是否归一化
      , copy_X=True # 是否copyX
      , max_iter=None # 最大迭代次数
      ,tol=0.001 # 结果的精度
      , solver='auto' # 计算方式
      , random_state=None # 设定随机模式
     )

# 案例：线性回归模型_波士顿房价数据集
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
X,y=load_boston(return_X_y=True)

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=9)

from sklearn.linear_model import Ridge
model_log=LinearRegression().fit(X_train,y_train)
print(model_log.score(X_train,y_train))

model_ridge=Ridge().fit(X_train,y_train)
print(model_ridge.score(X_train,y_train))

# 0.7176202687340321
# 0.7154454888738826

# 正则化系数选择的学习曲线_R2
alpha_range=np.linspace(1,500,50)
score_linear=[]
score_ridge=[]
for i in alpha_range:
    model_log=LinearRegression().fit(X_train,y_train)
    score_linear.append(model_log.score(X_test,y_test))
    model_ridge=Ridge(alpha=i).fit(X_train,y_train)
    score_ridge.append(model_ridge.score(X_test,y_test))

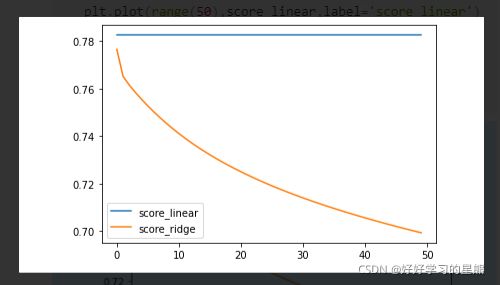
plt.plot(range(50),score_linear,label='score_linear')
plt.plot(range(50),score_ridge,label='score_ridge')
plt.legend()
plt.show()

# 正则化系数选择的学习曲线_MSE
alpha_range=np.linspace(1,100,100)
score_linear=[]
score_ridge=[]
for i in alpha_range:
    model_log=LinearRegression().fit(X_train,y_train)
    score_linear.append(cross_val_score(model_log,X_test,y_test,cv=5,scoring='neg_mean_squared_error').mean()*-1)
    model_ridge=Ridge(alpha=i).fit(X_train,y_train)
    score_ridge.append(cross_val_score(model_ridge,X_test,y_test,cv=5,scoring='neg_mean_squared_error').mean()*-1)

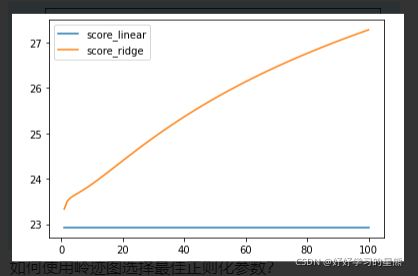
plt.plot(alpha_range,score_linear,label='score_linear')
plt.plot(alpha_range,score_ridge,label='score_ridge')
plt.legend()
plt.show()

结论：岭回归正则化下，正则化系数越大，MSE越大，越低，模型表现越差，说明模型几乎不存在多重共线性。

sklearn中自带的数据集基本不存在多重共线性。且通常情况下我们获取的数据集都不会有太大的多重共线性，所以岭回归实际的使用场景有限，且因为岭回归会进行特征过滤，模型也可能会因此效果变差。

---

如何使用岭迹图选择最佳正则化参数？（案例：希尔伯特矩阵）

什么是岭迹图：通过绘制不同的正则化系数α下，w的表现。选择较平稳的“喇叭口”时对应的正则化系数α，为最佳正则化系数。

但是岭迹图并没有对“平稳”定义，判断标准模糊，并不属于最佳正则化系数选择方案，所以了解即可。

---

代码案例：

from sklearn.linear_model import Ridge
X=1./(np.arange(1,11)+np.arange(0,10)[:,np.newaxis]) # 希尔伯特矩阵,如下图
# [:,np.newaxis]将一维数组变成n行1列的二维数组
y=np.ones(10)

n_alphas=200
alphas=np.logspace(-10,-2,n_alphas)
coefs=[]
for a in alphas:
    ridge=Ridge(alpha=a,fit_intercept=False).fit(X,y)
    coefs.append(ridge.coef_)

ax=plt.gca() # 没办法使用plt.figure()
ax.plot(alphas,coefs)
ax.set_xscale('log') # 横坐标显示为log
ax.set_xlim(ax.get_xlim()[::-1]) # 左右反转横坐标
# ax.axis('tight') #好像没有区别
plt.show()

---

如何在sklearn中使用linear_model.RidgeCV，带交叉验证的岭回归？（案例：波士顿房价数据集）

岭回归下，选择正则化系数最好的方式为交叉验证，所以sklearn提供了带交叉验证的岭回归RidgeCV，下面对RidgeCV的参数和使用方式进行案例演示，使用的数据集为波士顿房价数据集。

# 系数说明
RidgeCV (alphas=(0.1, 1.0, 10.0) # 正则化系数的取值
         , fit_intercept=True # 是否有截距项
         , normalize=False # 是否归一化
         , scoring=None # 评分方式，默认留一验证时使用R^2,否则返回均方误差（不论填什么都返回均方误差）
         , cv=None # 交叉验证次数，默认进行留一交叉验证
         , gcv_mode='auto' # 进行留一验证时，使用什么计算方法
         , store_cv_values=False # 是否保留交叉验证结果,cv=None时才保留
        )

# 属性
model.score(X,y) # 返回无交叉验证后的结果
model.cv_values_ # 返回所有交叉验证的结果，r^2或者MSE
model.alpha_ # 返回交叉验证结果最好时的alpha值

留一交叉验证是什么？

在交叉验证时，只留1条数据作为测试集，所以每条数据都会作为测试集。
留一交叉验证是岭回归交叉验证时最好的交叉验证方式。

？没懂的地方：scoring=None # 评分方式，默认留一验证时使用，否则返回均方误差
。
但是在操作过程中好像不论填什么都返回均方误差？ 为什么会这样，这个指标到底怎么用？ 

# 案例：带交叉验证的岭回归模型_波士顿房价数据集
from sklearn.linear_model import RidgeCV
from sklearn.datasets import fetch_california_housing as fch

X,y=fch(return_X_y=True)
ridge_cv=RidgeCV(alphas=np.linspace(1,1001,10)
#                  ,cv=5 # 如果不注这一行，则需要注掉store_cv_values
                 ,store_cv_values=True
                 ,scoring=None
                ).fit(X,y)

ridge_cv.score(X,y) # 返回无交叉验证后的结果

ridge_cv.cv_values_.mean(axis=0) # 返回所有交叉验证的结果

ridge_cv.alpha_ # 返回交叉验证结果最好的alpha值

---

如何理解Lasso，以及用Lasso进行特征选择？（案例：加利福尼亚房价数据集）

Lasso解决多重共线性的方法：通过在损失函数上添加w的1-范数乘以正则化系数α，其表达式为：

和岭回归一样，经过变化可得：

通过和岭回归对比可知，Lasso并不能通过调整保证存在，所以Lasso不能避免精确相关关系，只能限制高度相关关系。所以在使用时，如果线性回归无法求解，可以使用Lasso和岭回归调整；如果线性回归无解或者“除0错误”，只能使用岭回归调整。

---

在Lasso下，w求解的表达式为：

因为α可以人为设置，所以可以通过调整α，使得w为0。可以通过这种方法做特征选择，将w求解下系数为0的特征舍弃掉。

---

以下演示Lasso及特征选择：

# Lasso系数说明
Lasso(alpha=1.0 # 设定正则化系数
      ,fit_intercept=True # 是否有截距项，默认有
      ,copy_X=True # 是否复制X
      ,scoring=None # 设定评估指标
      ,normalize='deprecated' # 设定归一化方法
      ,max_iter=1000 # 设定最大迭代次数
      ,tol=0.001 # 设定精度
      ,random_state=None # 设定随机模式
      ,precompute=False # 是否加速计算，False则保持稀疏性
      ,warm_start=False # 重置fit
      ,positive=True # 为True时，求得的参数必须为正，把不为正的信息量放到截距项上。
      ,seleciton='cyclic' # 'random'时，每次迭代都随机，能加速迭代次数；cyclic为顺序迭代
     )

# Lasso特征选择（案例：对比ridge，加利福尼亚房价数据集）
from sklearn.linear_model import Lasso
X,y=fch(return_X_y=True)
alpha_range=np.linspace(0,2,20)
feature_lasso=[]
feature_ridge=[]
for a in alpha_range:
    model_lasso=Lasso(alpha=a).fit(X,y)
    feature_lasso.append((model_lasso.coef_!=0).sum())
    model_ridge=Ridge(alpha=a).fit(X,y)
    feature_ridge.append((model_ridge.coef_!=0).sum())
plt.plot(alpha_range,feature_lasso,label='feature_lasso')
plt.plot(alpha_range,feature_ridge,label='feature_ridge')
plt.legend()
plt.show()

model_ridge=Ridge(alpha=2).fit(X,y)
model_ridge.coef_

# array([ 4.36495800e-01,  9.43901106e-03, -1.06944092e-01,  6.43062429e-01,
#       -3.96430115e-06, -3.78617577e-03, -4.21284056e-01, -4.34455530e-01])

结论：随着正则化系数α的增大，系数为0的特征越来越多，当α＞1.75时，只剩下1个特征；而Ridge特征系数只会趋近于0，不会等于0。

---

如何在sklearn中使用linear_model.LassoCV，带交叉验证的Lasso？（案例：加利福尼亚房价数据集）

如果不希望alpha过大导致特征系数为0，应该如何设置alpha呢？

这时可以使用LassoCV中的eps和n_alphas参数调节正则化路径，从而使alpha以较小的路径变动，从而在调整alpha的时候，不使特征系数为0。

# 系数说明
from sklearn.linear_model import LassoCV

LassoCV(eps=0.001 # 正则化路径的长度
        ,n_alphas=100 # 正则化路径中的个数
        ,alphas=None # 设定alphas取值范围，如果输入了alphas，就不用输入eps和n_alpha
        ,cv=None # 交叉验证的折数
        ,fit_intercept=True # 是否有截距项
        ,normalize='deprecated' # 归一化方式
        ,copy_X=True # copyX
        ,max_iter=1000 # 最大迭代次数
        ,tol=0.0001 # 精度/阈值
        ,random_state=None # 随机模式
        ,precompute='auto' 
        ,positive=False
        ,selection='cyclic'
        ,verbose=False
        ,n_jobs=None
)
model.alpha_ # 返回交叉验证中最佳的alpha
model.alphas_ # 返回交叉验证中所有使用的alpha
model.coef_ # 返回模型的系数解
model.mse_path_ # 返回所有alpha及交叉验证的均方误差结果

# 使用正则化路径调整alpha的取值，以至于不让特征系数为0
from sklearn.datasets import fetch_california_housing
X,y=fetch_california_housing(return_X_y=True)
model=LassoCV(eps=0.0001
              ,n_alphas=200
              ,cv=9).fit(X,y)

model.alpha_
# 0.003221092661065102

model.alphas_

model.coef_
# array([ 4.24825188e-01,  9.65575964e-03, -8.44550706e-02,  5.25631726e-01,-3.09667549e-06, -3.73804407e-03, -4.17417323e-01, -4.28786474e-01])

model.mse_path_.mean()
# 0.90667071394857