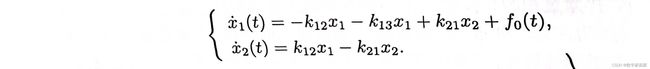《数学建模简明教程--基于python》学习笔记-第四章-微分方程-课后习题解答

先纵览一下题目,主要分为常微分方程的编程练习和建模两部分。

⭐️0.准备工作⭐️

# 通常的库
import numpy as np
import matplotlib.pyplot as plt
# 通用设置
plt.rc('font', family='SimHei')     # 显示中文字体
plt.rc('axes',unicode_minus=False)  # 显示负号
np.set_printoptions(precision=3, suppress=True)  # 设置print()时的小数位数为3，并关闭科学计数法
np.random.seed(2022)                # 设置随机数种子

# 比较重要的两个库
from scipy.integrate import odeint  # 求数值解 
import sympy as sp                  # 求解析解

• 关于 scipy.integrate下的odeint方法

  • integrate : 使…成整体;求…的积分
  • odeint(Integrate a system of ordinary differential equations) : 积分常微分方程组

• 关于sympy库的官方文档

  • 有时网速会非常慢

• 详细程序编写流程请看 1.编程练习-例 4.3 马尔萨斯人口改进模型

• 详细建模流程请看 2.应用练习-题1:介壳虫，澳洲瓢虫和DDT 和 3.拓展练习-艾滋病发展模型
  
  

1.编程练习

例4.2 容器漏水问题

求解析解

• 企图用sympy求该常微分方程的解析解

# 定义自变量
sp.var('t')
# 定义关于t的函数，或者说是因变量
h = sp.var('h', cls=sp.Function)
# 定义微分方程，这里要都移项到左边
eq = h(t).diff(t, 1) + 1.24*sp.sqrt(5)*sqrt(h(t))/(pi*(200*h(t)-h(t)**2))
# 求解微分方程
s1 = sp.dsolve(eq)

---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

 in 
      4 h = sp.var('h', cls=sp.Function)
      5 # 定义微分方程，这里要都移项到左边
----> 6 eq = h(t).diff(t, 1) + 1.24*sp.sqrt(5)*sqrt(h(t))/(pi*(200*h(t)-h(t)**2))
      7 # 求解微分方程
      8 s1 = sp.dsolve(eq)


NameError: name 'sqrt' is not defined

• 求解失败。
  因为这个微分方程是一阶非线性的齐次微分方程，对于非线性的微分方程很少会有解析解，所以我猜测这个微分方程要么没有解析解，要么就是这个模块求不出来。

求数值解

把微分方程左边只保留一阶导数,然后把右端项写成如下函数形式

• 定义未知函数可以用def也可以用lambda

dh = lambda h,t: - 0.62*np.sqrt(20*h)/np.pi*(200*h-h**2)

# def dh(h,t): 
#     return - 0.62*np.sqrt(20*h)/np.pi*(200*h-h**2) 

• 定义要求函数值的时间t的数组

t = np.arange(0, 0.02, 0.0001)  # 要求的数值点 [0,0.02) 左闭右开 间隔0.0001   根据实际情况调整

• 用odeint函数求解这个常微分方程组的数值解，并且设置初始值为100,指t[0]时刻。

s1 = odeint(dh, 100, t)         # 采用龙格库塔方法求解，一般默认是四阶的方法。

关于龙格库塔方法的简单介绍可以参考mooc浙江大学的常微分方程的第八章-数值常微分方程入门。

• 绘制图像

plt.plot(t, s1)  # 绘制水面高度随着时间的变化曲线
plt.grid()

注意:Python只能求解一阶常微分方程组或方程组的数值解，高阶常微分方程必须转化成一阶方程组。

如果你忘记怎么转化了，可以参考mooc中天津师范大学的常微分方程-第五章-第一节。

ps:讲得还蛮不错的!

例4.3 马尔萨斯人口改进模型

求数值解

1.取定相关参数值

m = 10000   
r = 0.2

m: 人口增长数量
r: 固有增长率

2.以函数形式定义常微分方程

dx = lambda x,t: r*(1 - x/m)*x

3.定义要求的时间范围

t = np.arange(0, 100, 1)

4.调用odeint函数来求解常微分方程的数值解

• 初值条件:其中第二个参数值100对应t[0]时对应的初值。

X = odeint(dx, 100, t)

• 返回值的类型时一个数组，这里用X来承接每个t时刻的人口数x,

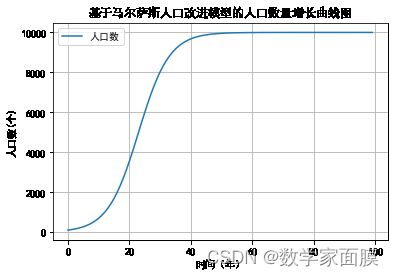
5.绘制人口x随t的变化图

plt.plot(t, X)
plt.grid()
# 装饰性函数
plt.legend(['人口数'])
plt.xlabel('时间（年）')
plt.ylabel('人口数(个)')
plt.title('基于马尔萨斯人口改进模型的人口数量增长曲线图')

Text(0.5, 1.0, '基于马尔萨斯人口改进模型的人口数量增长曲线图')

求解析解

r = 0.1
m = 10000

1.定义自变量和未知函数

sp.var('t')  # 自变量
x = sp.var('x', cls=sp.Function)  # 未知函数

• 注意写入微分方程时，右端项全部写到左边。

2.定义微分方程

eq = x(t).diff(t,1) - r*(1 - x(t)/m)*x(t)

• x(t).diff(t,1) :表示一阶导数
• differentiate: 求导

3.初值条件

con = {x(0):100}

4.求解微分方程

s = sp.dsolve(eq, ics=con)  # ics承接初始条件
print(s)

Eq(x(t), -10000.0/(-1.0 - 99.0*exp(-0.1*t)))

• ics(initial conditions):初始条件,下图取自官方文档。

• 查看一下dsolve函数的返回值s的参数

s.args

(x(t), -10000.0/(-1.0 - 99.0*exp(-0.1*t)))

• 求t=10时的函数值

s.evalf(subs={t:10})  

$x\left(10\right)=267.236309893952$

s.evalf(subs={t:10}).args[1]  

$267.236309893952$

s.subs(t,10)  # 或者

$x\left(10\right)=267.236309893952$

• 绘制函数时需要输入s.args[1](等式的右端项)

s.args[1] 

$-\frac{10000.0}{-1.0-99.0e^{-0.1t}}$

看一下s.args[1]的类型

print(type(s.args[1]))

sp.Mul(x,x) : 乘法

5.绘制函数图像

• 求出解析解后绘制函数图像和求出数值解后绘制函数图像是不一样的

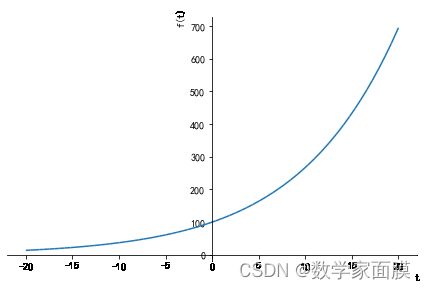
5.1 用sp模块的plot函数绘制图像

sp.plot(s.args[1], (t,-20,20))

• 参数值(t,-20,20)表示定义域，t是自变量
  

关于sp.plot的官方文档

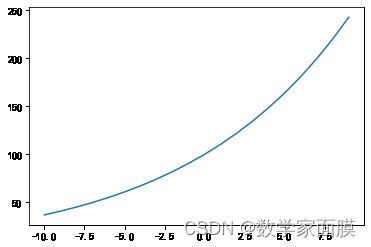
5.2 或用evalf函数先生成一些值，然后再用matplotlib绘制

# 生成[-10,9]的函数值
ls = []
for i in range(-10,10):
    ls.append(s.evalf(subs={t:i}).args[1])

# 用matplotlib绘制函数图像
plt.plot(range(-10,10), ls)
plt.show()

例4.4 药物在体内分布与排除问题

• 必要的说明:
  题目中还根据$x_i(t)$与血药浓度c_i(t)、房室容积$V_i$之间的关系式$x_i(t)$ = $V_i{c}_i(t),i=1，2，$
  进一步把两个房室的质量关于时间的动力系统转化为两个房室的浓度关于时间的动力系统，
  本质是一样的，所以我就选择前者进行求解！

求解析解

sp.var('t')
x,y = sp.var('x,y', cls=sp.Function) # 未知函数 中心室和周边室内的药物质量
f = 2*sp.exp(-2*t)  # 关于时间t的给药函数 我用指数分布函数E（2）来模拟

k12 = 1  # 药物由中心室流向周边室的速率系数            
k21 = 3  # 药物由周边室流向中心室的速率系数
k13 = 2  # 药物由中心室排除的速率系数 

• 然后根据二室模拟示意图建立常微分方程组。注意全部写到等式左边。

eqs = [x(t).diff(t) - (- k12*x(t) - k13*x(t) + k21*y(t) + f),
       y(t).diff(t) - (k12*x(t) - k21*y(t))]

# 定义初值条件
con = {x(0):100, y(0):5}
# 求解微分方程组
s = sp.dsolve(eqs, ics = con)  #; print(s.args[1])

s  # 是一个列表，里面有关于两个未知函数的等式

[Eq(x(t), (101 - 6*sqrt(3))*exp(-t*(sqrt(3) + 3))/2 + (6*sqrt(3) + 101)*exp(-t*(3 - sqrt(3)))/2 - exp(-2*t)),
 Eq(y(t), (18 - 101*sqrt(3))*exp(-t*(sqrt(3) + 3))/6 + (18 + 101*sqrt(3))*exp(-t*(3 - sqrt(3)))/6 - exp(-2*t))]

sp.plot(s[0].args[1],s[1].args[1], (t, -5, 5))  

• 参数说明
  s[0].args[1] 是第一个函数。
  s[1].args[1] 是第二个函数。
  (t, -5, 5) 是上面两个函数的范围。
  
  

求数值解

# 定义相关参数值
k12 = 1
k21 = 3.6
k13 = 10
m = 10000 
r = 0.2

• 关于时间t的给药函数,我用正弦型函数来模拟

# 定义给药函数
f = lambda t:200*np.sin(t)  

# 定义微分方程组
d = lambda x,t:[- k12*x[0] - k13*x[0] + k21*x[1] + f(t),
                   k12*x[0] - k21*x[1]]
# 求[0,99)的未知函数的数值解
t = np.arange(0, 100, 1)
s1 = odeint(d, [100,300], t)

# 绘制函数图像
plt.plot(t, s1)
plt.grid()
plt.legend(['中心室', '周边室'])
plt.title('中心室和周边室的药物质量随时间变化的曲线图')

Text(0.5, 1.0, '中心室和周边室的药物质量随时间变化的曲线图')

发现由于排药物速度较快，药物浓度迅速下降，由于给（gei）药函数是正弦型函数，所以连个室的药物质量也呈现出了近似的波动，

此外由于药物是仅仅从中心排出体外，故中心室的浓度要低一些。

2. 应用练习

前面的题目都已经建立好模型了，只要代码实现就可以了，但下面的题目就要自己想办法建立模型了，会有更大的挑战，但其实也不难。

题1：介壳虫，澳洲瓢虫和DDT

1.模型假设

• 介壳虫和澳洲瓢虫在独立的正常环境下都会呈现S型增长曲线。
• 引入的澳洲瓢虫要吃的介壳虫数量和澳洲瓢虫的数量呈正比。
• 介壳虫的数量对于澳洲瓢虫的增长没有影响。
• DDT 杀死介壳虫和澳洲瓢虫的速率都和它们的数量呈正比。
• DDT会杀死介壳虫，但不会影响没有活着的介壳虫的正常繁殖。

2.符号说明

符号	含义
k21	每只澳洲瓢虫吃的介壳虫数量
k31	单位时间DDT杀死的介壳虫的比例
k32	单位时间DDT杀死的澳洲瓢虫的比例
r1	介壳虫的固有增长率
r2	澳洲瓢虫的固有增长率
m1	介壳虫的最大可持续容量
m2	澳洲瓢虫的最大可持续容量

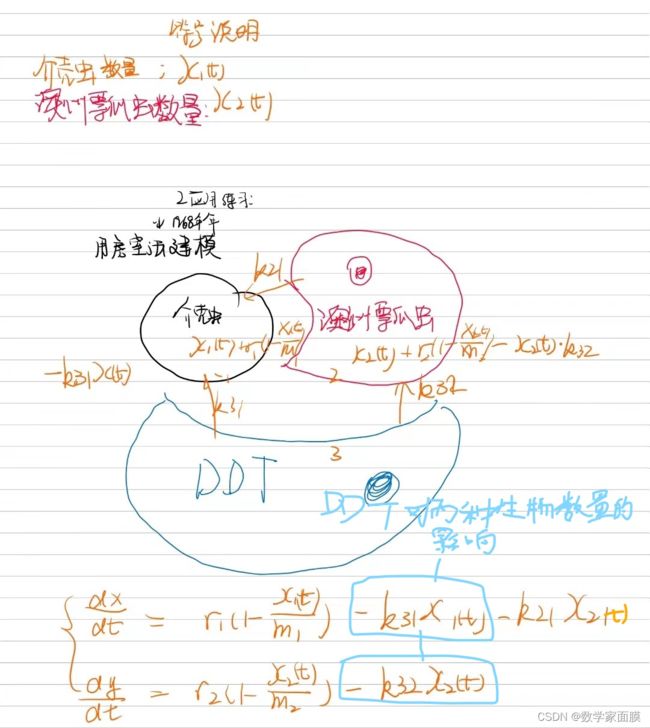
3.模型建立

下图是我第一次微分方程建模手稿，主要运用书中介绍的房室建模法。

• 由于美国首先是引入天敌澳洲瓢虫，后来檬园主才使用DDT，故不妨以开始使用DDT为界限分为前后两个时间段，分别建立微分方程。

• 第一阶段（引入澳洲瓢虫）

根据假设条件写出介壳虫和澳洲瓢虫的数量$X_1(t)$,$X_2(t)$所满足的微分方程。

$X_1(t)$的变化率由自身的逻辑斯蒂增长速率$r_1(1-\frac{X_1(t)}{m_1})$、单位时间自身被澳洲瓢虫吃掉的数量$-k_{21}{X}_2$组成，$X_2(t)$的变化率仅由自身的逻辑斯蒂增长速率$r_2(1-\frac{X_2(t)}{m_2})$。于是有

$$\{\begin{array}{l}\frac{d{X}_1}{dt}=r_1(1-\frac{X_1}{m_1})-k_{21}{X}_2,\\ \frac{d{X}_2}{dt}=r_2(1-\frac{X_2}{m_2}),\end{array}$$

• 第二阶段（使用DDT）

考虑被DDT杀死的介壳虫和澳洲瓢虫的数量$-k_{31}{X}_1$，$-k_{32}{X}_2$。

$$\{\begin{array}{l}\frac{d{X}_1}{dt}=r_1(1-\frac{X_1}{m_1})-k_{21}{X}_2-k_{31}{X}_1,\\ \frac{d{X}_2}{dt}=r_2(1-\frac{X_2}{m_2})-k_{32}{X}_2,\end{array}$$

4.模型求解

4.1 确定参数

先求第一阶段的方程的数值解，采用的一组参数如下:
k21 = 0.2只/天
k31 = 0.1/天
k32 = 0.5/天
r1 = 0.2/天
r2 = 0.2/天

最大可持续容量:
m1 = 1000只
m2 = 1000只
两个种群的初始数量都是300只

• 对于采取这些参数的理由理应是要加以说明的，但是限于时间和学识，我选取了一组使得结果与题目描述较符合的参数。

编写程序如下:

k21 = 0.2
k31 = 0.1
k32 = 0.5
r1 = 0.2 
r2 = 0.2
# 最大可持续容量
m1 = 1000
m2 = 1000

4.2 第一阶段

d1 = lambda x,t1:[r1*(1 - x[0]/m1)*x[0]  - k21*x[1],r2*(1 - x[1]/m2)*x[1]]   # 要把x[1]加上 不然就只是环比增长率（无单位） 而不增长速率 

t1 = np.arange(0, 10, 0.01)
s1 = odeint(d1, [300,300], t1)

plt.plot(t1, s1)
plt.grid()
plt.legend(['介壳虫', '澳洲瓢虫'])

s1[199] 

array([242.4  , 389.528])

• 可以看到引进澳洲瓢虫还是有一定的效果的。
• 选取第2天为分界点，以第二天的介壳虫和澳洲瓢虫的数量作为第二阶段的初始条件。
• 介壳虫242只。
• 澳洲瓢虫390只。

4.3 第二阶段

m = 10000 
r = 0.2
d2 = lambda x,t2:[r1*(1 - x[0]/m1)*x[0] - k31*x[0] - k21*x[1],
                   r2*(1 - x[1]/m2)*x[1] - k32*x[1]]

t2 = np.arange(2, 40, 0.01)
s2 = odeint(d2, [242,390], t2)

plt.plot(t2, s2)
plt.grid()
plt.legend(['介壳虫', '澳洲瓢虫'])

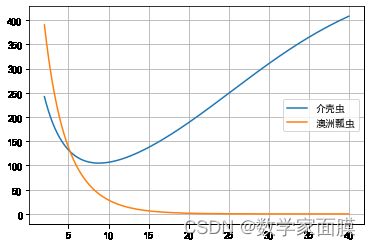
5.两阶段合并和结果分析

• 将两个阶段的生物数量变化绘制在一起，凸显出加入DDT后，首先在澳洲瓢虫数量还没有太少时，介壳虫在澳洲瓢虫和DDT的双重压力下快速下降，但是又由于DDT对澳洲瓢虫的致死率更大，故在澳洲瓢虫的数量进一步减少时，介壳虫又凭借自生顽强的生命力和抗DDT性又死灰复燃。介壳虫增加起来，澳洲瓢虫反而减少了。

plt.plot(np.arange(0,39.99,0.01), np.r_[s1[:199],s2])  # 两个阶段的时间和数量 s[199]数量四舍五入和s2[0]是一样的，避免重复故切片取到199（不包含199）
plt.legend(['介壳虫', '澳洲瓢虫'])
plt.annotate('DDT"大显身手"', xy=(2, 380), xytext=(12.5, 250),
             arrowprops=dict(arrowstyle="->",connectionstyle="angle3,angleA=0,angleB=-90"), 
             horizontalalignment='center',verticalalignment ='bottom', fontsize=20)
plt.annotate('介壳虫:我又行了', xy=(8, 110), xytext=(20, 10),
             arrowprops=dict(arrowstyle="->",connectionstyle="angle3,angleA=0,angleB=-90"), 
             horizontalalignment='center',verticalalignment ='bottom', fontsize=20)
plt.legend(['介壳虫', '澳洲瓢虫'])

• 该数学模型基本可以解释这个现象了。

题2：白蚁和批发虫的共生演化模型

• 使用模拟近似法建模。

白蚁和披发虫时一个共生的关系，故不妨套用已有的共生演化模型。

求解析解

sp.var('t')
x,y= sp.var('x,y', cls=sp.Function)

N1 = 100
N2 = 100
r1 = 0.2  # 白蚁
r2 = 0.1

• a21和a12为共生作用系数，当共生作用系数之和均为负时，系统属于互惠共生模式演化。

a21 = -0.3
a12 = -0.3

eqs = [x(t).diff(t) - r1*x(t)*(1 - x(t)/N1 - a21*y(t)/N2),
      y(t).diff(t) - r2*y(t)*(1 - y(t)/N2 - a12*x(t)/N1)]

• 运用程序无法求出解析解。

# sp.dsolve(eqs)  # 运行后会卡死

• 参考文献：
  [1]张影,高长元,王京.跨界创新联盟生态系统共生演化模型及实证研究[J/OL].中国管理科学:1-14[2022-05-30].DOI:10.16381/j.cnki.issn1003-207x.2019.0314.

• 这时应该进行平衡点分析（不用求出解析解）。

求数值解

d = lambda x,t:  [r1*x[0]*(1 - x[0]/N1 - a21*x[1]/N2),
       r2*x[1]*(1 - x[1]/N2 - a12*x[0]/N1)]

t = np.arange(0, 100, 1)
s1 = odeint(d, [100,100], t)

plt.plot(t, s1)
plt.grid()
plt.legend(['白蚁', '披发虫'])

题3：捕鱼模型

题3-1 鱼儿数量的和时间的数学模型

• 在逻辑斯谛方程基础上，在右端添加$EX(t)$即可，E表示捕捞率或捕捞强度。

解析解

• 定义未知函数和自变量

sp.var('t')
x = sp.var('x', cls = sp.Function)

• 定义相关参数取值

E = 0.1 # 捕捞率
m = 1000  # 鱼量上限
r = 0.1

• 定义微分方程

eq = [x(t).diff(t) - r*(1 - x(t)/m) + E*x(t)]  # 注意右端项移到左边要变号

• 求解

s1 = sp.dsolve(eq, ics = {x(0):100})

• 绘图

sp.plot(s1[0].args[1])

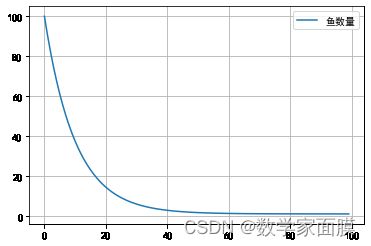
数值解

# 定义微分方程
dx = lambda x,t: r*(1 - x/m) - E*x  # 一个等式时不要加[]
# 定义要求的时间点
t = np.arange(0, 100, 1)
# 调用odeint函数求数值解
s1 = odeint(dx, 100, t)
# 绘制鱼儿数量的变化图像
plt.plot(t, s1)
plt.grid()
plt.legend(['鱼数量'])

题3-2 小鱼儿重量和时间的数学模型

假设鱼为球体，体积为V，表面积为S，半径为R，初始重量为$G_0$,鱼的密度为$\rho$,没有考虑捕鱼。

详细建模过程可参考 最优捕鱼模型。

模型把鱼假设成一个球体，讲道理我不太能接受，如果假设成一个圆柱体，长方体，扁的椭球，那又该怎么建立模型呢？

# 设定参数值
k1 = 0.5
k2 = 0.1
b = 1
# 定义微分方程 # 
dG = lambda G,t: k1*b*G**(2/3) - k2*G   # 一个等式时不要加[]
# 定义要求的时间点
t = np.arange(0, 100, 1)
# 求解，其中100为初始条件
s1 = odeint(dG, 100, t)
# 绘图
plt.plot(t, s1)
plt.grid()
plt.legend(['鱼重量'])

3.拓展练习

艾滋病发展模型

1.问题分析

题目要求考虑至少易感染人群，被HIV感染人群，接种疫苗的人群，接种疫苗后又被感染的人群，已患艾滋病的人群。此外我还考虑了死亡人群。通过对比是否打疫苗，比较不同人群被HIV感染的情况，建立在有疫苗情况下的艾滋病传播模型。模型主要在SEIR模型的基础上修改得到新的模型，其中将康复人群替换为死亡人群，并且把潜伏人群和易感人群按照是否打过疫苗各分为两类以研究疫苗的作用。

2.初步的模型假设

（1）假设这里的E，VE和I人群都具有相同传染能力。
（2）易感人群向接种疫苗的人群的转化速率和易感人群数量成正比。
（3）疫苗在人发病后不再起作用。
（4）没有康复人群。
（5）假设E，VE，I接触到的人群中S和VS的比例和总人群中S和VS的比例一样。

3.符号说明

• 我这里用Vaccinated:打疫苗的，表明接种疫苗的易感人群VS，和被HIV感染的疫苗人群VE。
  S:易感人群数量
  VS:接种疫苗的人群数量
  E:未打疫苗的潜伏者数量
  VE:打了疫苗的潜伏者，或者说被HIV感染的疫苗人群数量
  I:发病人群数量
  G:死亡人群数量
  N:初始人口数

• 下图是模型示意图

4.完善模型假设

a还需要假设一个区域内总人数为 N - G，即N - G = S + VS + E + VE + I ，
每天每位感染者(E,VE,I)接触的人数为 P，
健康人比例为 (S + VS)/(N - G)，
其中易感人群S按照比例 A 转化为潜伏人群E，
潜伏人群E按照比例 C 转化为发病人群，
发病人群按照比例 g 转化为死亡人群。

易感人群S按照比例k转化为接种疫苗的人群VS，
接种疫苗的人群VS按照比例B转化为打了疫苗的潜伏着VE，
打了疫苗的潜伏着VE按照比例D转化为发病人群I。

5.模型建立

此时，在该艾滋病传播模型上可以建立如下微分方程:

$$\{\begin{array}{l}\frac{dS}{dt}=-(E+VE+I)p\frac{S}{N-G}A-kS,\\ \frac{dVS}{dt}=-(E+VE+I)p\frac{VS}{N-G}B+kS,\\ \frac{dE}{dt}=(E+VE+I)p\frac{S}{N-G}A-CE,\\ \frac{dVE}{dt}=(E+VE+I)p\frac{VS}{N-G}B-D\ast VE,\\ \frac{dI}{dt}=CE+D\ast VE-gI,\\ \frac{dG}{dt}=gI,\end{array}$$

我参考了该论文的SEIR模型的建立

6.用程序进行模型求解

# 设置参数
N = 10000
A = 0.2
B = 0.1
k = 0.1  # 剩下的都是不肯打疫苗的顽固分子 或者不符合条件
C = 0.1
D = 0.1
g = 0.0655
p = 0.3  # 密切接触0.3个人 
# 定义微分方程组
d = lambda x,t: [-(x[4] + x[2] + x[3])*p*x[0]/(N-x[5])*A - k*x[0],
                            k*x[0] - (x[4] + x[2] + x[3])*p*x[1]/(N-x[5])*B,
                            (x[4] + x[2] + x[3])*p*x[0]/(N-x[5])*A - C*x[2],
                            (x[4] + x[2] + x[3])*p*x[1]/(N-x[5])*B - D*x[3],
                             C*x[2] + D*x[3] - g*x[4],
                             g*x[4]
                            ]
# 定义求解范围
t = np.arange(0, 800, 1)
# 设置初始条件并求解
s1 = odeint(d, [4500,4500,500,500,0,0], t)
# 绘制函数
plt.plot(t, s1)
plt.grid()
plt.legend(['S','VS','E','VE','I','G'])
    #对应  x[0] x[1] x[2] x[3] x[4] x[5]

死亡率太高，传染速度没死亡率高，所以被感染的都死了，就没有可以继续感染的人了。。。。。

通过调整不同参数，会得到不同结果，对应不同的情况。

4.学习感慨

时光飞逝，自从我把常微分方程作为下一个学习目标，不知不觉已然近两个月过去了。虽然临近期末，但我还是完成了它，因为它是重要的！

5.学习困惑

• 对于我最后建立的艾滋病传播模型怎么进行模型的稳定性分析?
• 怎么求解偏微分方程?
• 关于题3-2，模型把鱼假设成一个球体，讲道理我不太能接受，如果假设成一个圆柱体，长方体，扁的椭球，那又该怎么建立模型呢？
• 由于网上信息爆炸，想要准确获得自己想要的学习资源，找到优质的学习视频，不可避免要花更多的时间，请问能否建立模型分析花多少时间找学习资源的性价比最高？