给定一个函数 \(f(x)=x^2+3x-10\),完成以下题目:
理解方程求根中的二分法(Bisection),并使用基本的 numpy 库而非 scipy 库,来实现算法。
非线性方程求根
注:该部分内容参考的是「中南大学数学科学与计算机技术学院」的课件,介绍了二分法的背景和原理,不感兴趣的可略过。
在科学研究和工程设计中, 经常会遇到的一大类问题是非线性方程 f(x)=0 的求根问题,其中 f(x) 为非线性函数。方程f(x)=0的根, 亦称为函数f(x)的零点。如果 f(x) 可以分解成 \(f(x)=(x-x^{*})^{m}g(x)\),则称 \(x^{*}\) 是方程 f(x)=0 的 m 重根。
当 f(x) 不是 x 的线性函数时,称对应的函数方程为非线性方程。如果 f(x) 是多项式函数,则称为代数方程,否则称为超越方程(三角方程,指数、对数方程等)。一般称 n 次多项式构成的方程
\[a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x^{1}+a_{0}x^{0}=0\]
为 n 次代数方程,当 n>1 时,方程显然是非线性的。
一般稍微复杂的 3 次以上的代数方程或超越方程,很难获得无法求得精确解。下面将介绍常用的求解非线性方程的近似根的一种数值解法。
通常方程根的数值解法大致分为三个步骤进行:
判定根的存在性。即方程有没有根?如果有根,有几个根?
确定根的分布范围。即将每一个根用区间隔离开来,这个过程实际上是获得方程各根的初始近似值。
根的精确化。将根的初始近似值按某种方法逐步精确化,直到满足预先要求的精度为止。
二分法是求解方程近似根的一种常用的简单方法。
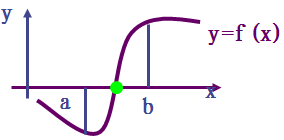
设函数 f(x) 在闭区间 [a,b] 上连续,且 \(f(a)f(b)<0\),根据连续函数的性质可知,f(x)=0 在 (a,b) 内必有实根,称区间 [a,b] 为有根区间。为明确起见,假定方程 f(x)=0 在区间 [a,b] 内有唯一实根 \(x^{*}\)。
二分法的基本思想是:首先确定有根区间,将区间二等分,通过判断 f(x) 的符号,逐步将有根区间缩小,直至有根区间足够地小,便可求出满足精度要求的近似根。
对于代数方程,其根的个数(实或复的)与其次数相同。至于超越方程,其根可能是一个、几个或无解,并没有什么固定的圈根方法求方程根的问题。求方程根的问题,就几何上讲,是求曲线 y=f(x) 与 x 轴交点的横坐标。
设 f(x) 为区间 [a,b] 上的单值连续, 如果\(f(a)·f(b)<0\) , 则 [a,b] 中至少有一个实根。如果 f(x) 在 [a,b] 上还是单调地递增或递减,则仅有一个实根。
大体确定根所在子区间有两种方法:
1、 画图法
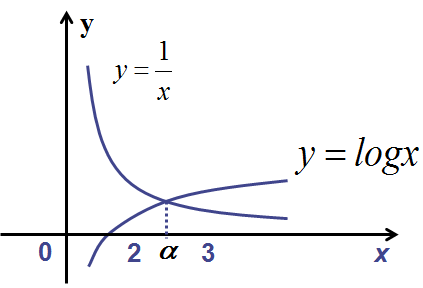
画出 y=f(x) 的图,从而可以看出曲线和 x 轴交点的大致位置。也可以将 f(x)=0 分解成 \(\varphi_{1}(x)=\varphi_{2}(x)\) 的形式,\(\varphi_{1}(x)\) 与 \(\varphi_{2}\) 两曲线交点的横坐标所在的区间为含根区间,例如 \(xlogx-1=0\),可以改写为 \(logx=\frac{1}{x}\),画出对数曲线 \(y=logx\),与双曲线 \(y=\frac{1}{x}\),它们交点的横坐标位于区间 [2,3] 内。
2、 逐步搜索法
对于给定的 f(x),设有根区间 [A,B],从 \(x_{0}=A\) 出发,以 h=(B-A)/n(n是正整数) 为步长,在 [A,B] 内取定节点:\(x_{i}=x_{0}+ih(i=0,1,2,...,n)\),从左至右检查 \(f(x_{i})\) 的符号,如发现 \(x_{i}\) 与端点 \(x_{i-1}\) 的函数值异号,则得到一个缩小的有根子区间 \([x_{i-1},x_{i}]\)。
用逐步搜索法进行实根隔离的关键是选取步长 h, 要选择适当 h,使之既能把根隔离开来,工作量又不太大。为获取指定精度要求的初值,可在以上隔离根的基础上采用对分法继续缩小该含根子区间。二分法可以看作是搜索法的一种改进。
二分法求根
二分法是逐次把有根区间分半,直到找到根或有根区间的长度小于给定精度为止。
二分法步骤:
(1) 计算函数 f(x) 在区间 [a,b] 中点的函数值 \(f(\frac{a+b}{2})\),并做下面的判断:
如果 \(f(a)f(\frac{a+b}{2})<0\),转到(2);
如果 \(f(a)f(\frac{a+b}{2})>0\),令 \(a=\frac{a+b}{2}\),转到(1);
如果 \(f(a)f(\frac{a+b}{2})=0\),则 \(x=\frac{a+b}{2}\) 为一个根。
(2) 如果 \(|a-\frac{a+b}{2}|<\varepsilon\)(\(\varepsilon\) 为预先给定的精度),则 \(x=\frac{3a+b}{4}\) 为一个根,否则令 \(b=\frac{a+b}{2}\),转到(1)。
下面在 Python 中编程实现二分函数 HalfInterval。
功能:用二分法求函数在某个区间上的一个零点。
调用格式:root = HalfInterval(f, a, b, eps)
其中,f 为函数名,a 为区间左端点,b 为区间右端点,eps 为根的精度,root 为求出的函数零点。
注意:这里我们假定方程 f(x)=0 在区间 [a,b] 内有唯一实根,\(f(a)·f(b)<0\),HalfInterval 求出的也是该区间内的一个实根。如果要求出 f(x)=0 的所有根,则首先应用画函数图或逐步搜索的方法确定各个根所在的区间,再在各区间内使用二分法求根。
def HalfInterval(f, a, b, eps): # f 为函数名,a 为区间左端点,b 为区间右端点,eps 为根的精度
midValue = (a + b)/2.0 # 此处必须是 2.0,不能是 2
if f(a)==0: # 先看根是不是在两个边界上
root = a
elif f(b)==0:
root = b
elif f(a)*f(b)>0: # 排除区间内没有根的情况
root = False
elif f(midValue)==0: # 检查下中间值是不是根
root = midValue
elif f(a)*f(midValue)<0: # 根在区间前半部分
if (midValue - a)使用上述算法来得到函数 f(x) 的根。
要求的函数是 \(x^{2}+3x-10\),该函数的根可以通过分解因式方法求得 \(x^{2}+3x-10=(x-2)(x+5)\),解为 2 和 -5。
或者使用 Python 的数学符号计算库 SymPy 求函数的根。
import sympy
from sympy.abc import x # SymPy 是 Python 的数学符号计算库,用它可以进行数学公式的符号推导。
fsym = x**2+3*x-10
sympy.solve(fsym) # Sympy 可以帮助我们求解方程[-5, 2]可以用 scipy.optimize 中的 bisect 或 brentq 求根。
import scipy.optimize as opt
print (opt.bisect(f, -10, 0), opt.bisect(f, 0, 5))
print (opt.brentq(f, -10, 0), opt.brentq(f, 0, 5))(-5.0, 1.9999999999998863)
(-5.0, 2.0)现在我们用二分法求解,然后再跟上面的解作比对。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinef = lambda x: x**2+3*x-10 # 定义一个匿名函数先画出函数图形,看下函数的根出现在哪些区间。
x = np.linspace(-10, 10, 1000) # 先生成 1000 个 x
y = f(x) # 对应生成 1000 个 f(x)
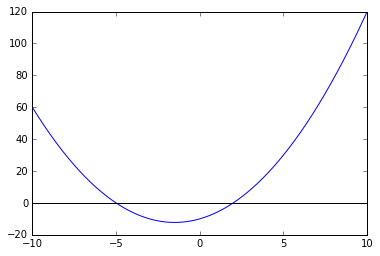
plt.plot(x, y); # 看一下这个函数长什么样子
plt.axhline(0, color='k'); # 画一根横线,位置在 y=0由上图可知,函数 \(x^{2}+3x-10\) 有两个零点,分别在 [-10,0] 和 [0,5] 两个区间内。
然后我们使用上面 HalfInterval 函数求出这两个区间的根。
root1 = HalfInterval(f, -10, 0, 0.001)
root2 = HalfInterval(f, 0, 5, 0.001)
print (root1,root2)(-5.0, 1.99981689453125)可见,上面求出的两个根与真正的根 -5 和 2 差别不大,比较精确。
理解梯度下降法(Gradient descent),并使用基本的 numpy 库而非 scipy 库,来实现算法。
梯度下降法和课程中用到的最小二乘法都可用于最小化误差平方和,但两者的实现思路是不一样的。最小二乘是一种纯数学方法,把所有数据组成矩阵方程来解出未知参数,而梯度下降法是把误差平方和作为一个函数,求极值,误差平方和包含了所有的数据。
\[\sum_{i=1}^{N}(y^{(i)}-\theta_{0}-\theta_{1}x^{(i)})^2\]
梯度下降法用来最小化误差平方和,和求函数极值,是一回事儿。本题就是用来求函数极值。
梯度下降法是求解无约束最优化问题的一种最常用的方法,有实现简单的优点。梯度下降法是迭代算法,每一步需要求解目标函数的梯度向量。
假设 f(x) 是 \(R^{n}\) 上具有一阶连续偏导数的函数,要求解的无约束最优化问题是
\[\operatorname*{min}\limits_{x \in R^{n}}f(x)\]
\(x^{*}\) 表示目标函数 f(x) 的极小点,注意这里的 x 相当于上面误差平方和式子中的未知参数 \(\theta\)。
梯度下降法是一种迭代算法,选取适当的初值,不断迭代,更新 x 的值,进行目标函数的极小化,直到收敛。由于负梯度方向是使函数值下降最快的方向,在迭代的每一步,以负梯度方向更新 x 的值,从而达到减少函数值的目的。
梯度下降法算法如下:
输入:目标函数 f(x),梯度 \(\nabla f(x)\),计算精度 \(\varepsilon\);
输出:f(x) 的极小点 \(x^{*}\)。
(1) 取初始值 \(x^{(0)} \in R^{n}\),置 k=0
(2) 置 \(x^{(k+1)}=x^{(k)}-\lambda\nabla f(x^{(k)})\),计算 \(f(x^{(k+1)})\)
(3) 当 \(||f(x^{(k+1)})-f(x^{(k)})||<\varepsilon\) 时,停止迭代,令 \(x^{*}=x^{(k+1)}\);否则,置 k=k+1,转 (2)。
其中 \(\lambda\) 是步长,也称学习率,步子小了收敛慢,步子大了容易跳过收敛值,然后在收敛值附近震荡。
当目标函数是凸函数时,梯度下降法的解释全局最优解,一般情况下,其解不保证是全局最优解。
一维梯度下降
def Gradientdescent(f, xk, lamda, deltaf, epsilon): # 一维梯度下降法代码,f 是函数,xk 是初始值,lambda 是步长,deltaf 是导数,epsilon 是精度
xknew = xk - lamda * deltaf(xk)
if abs(f(xknew)-f(xk))上面的代码中的自变量 x 为一维变量。为避免每次递归调用都求导,就要求在调用之前就求出导函数。
上面的代码比较麻烦的是求导函数,Python 有个数学符号计算库 SymPy,可以进行数学公式的符号推导,可用于求导。@lyltj2010 提供了清晰简练的梯度下降代码,太值得学习了。代码如下所示。
# lyltj2010 的代码
import sympy
from sympy.abc import x
fsym = x**2 + 3*x - 10
def gd(fsym,x0,step=0.01,tol=1e-5):
x1 = x0
while True:
x0 = x1
x1 = x0 - step * fsym.diff().subs(x,x0)
if np.abs(x1-x0) < tol:
break
return x1
print gd(fsym,-1)-1.49951076900151多维梯度下降
上面介绍的是 x 为一维变量的情况,x 也可以为多维变量,这时 x 是一个向量。
要找到使 f(x) 最小的 x 向量,首先给 x 向量赋个初值,然根据梯度下降法不断更新 x 向量的每个元素。
\[x_{k+1}=x_{k}-\lambda\frac{\partial}{\partial x_{i}}f(x)\]
其中 \(\lambda\) 跟上面一样是步长,也称学习率,步子小了收敛慢,步子大了容易跳过收敛值,然后在收敛值附近震荡。
多维梯度下降的 Python 代码会复杂得多,关于二维梯度下降,这里强烈推荐 @lyltj2010 的代码,简洁、优雅、严谨,学习典范!
import sympy
from sympy.abc import x,y
# lyltj2010 的代码
def gd_2d(f,X,step=0.01,tol=1e-3):
X0 = X
def gradient(f,X):
dx = float(f.diff(x).subs({x:X[0], y:X[1]}))
dy = float(f.diff(y).subs({x:X[0], y:X[1]}))
norm = (1./np.sqrt(dx**2+dy**2))
return norm*np.array([dx,dy])
while True:
z0 = float(f.subs({x:X0[0], y:X0[1]}))
X1 = X0 - step*gradient(f,X0)
z1 = float(f.subs({x:X1[0], y:X1[1]}))
if np.abs(z1 - z0) < tol:
break
X0 = X1
return X1def gsym(x,y):
return (x-1)**4 + 5 * (y-1)**2 - 2*x*y
print gd_2d(gsym(x,y),[0,0]) [ 1.88360394 1.37674131]使用 minimize 求对应的最小值。
def g(X):
x,y = X
return (x-1)**4 + 5 * (y-1)**2 - 2*x*y
X_opt = opt.minimize(g, (8, 3)).x # (8,3) 是起始点
print X_opt[ 1.88292611 1.37658521]结果跟二维梯度下降差不多,足够精确。
使用上述算法来得到函数 f(x) 的最小值。
在上面已经定义了匿名函数 \(f(x)=x^2+3x-10\),关于求函数极值的讨论可参考任意一本微积分教材,这里不再详细介绍。
从函数的图形可以看出,f(x) 只有一个极小值。
x = np.linspace(-10, 10, 1000) # 先生成 1000 个 x
y = f(x) # 对应生成 1000 个 f(x)
plt.plot(x, y); # 看一下这个函数长什么样子
plt.axhline(0, color='k'); # 画一根横线,位置在 y=0求导数 \(f^{'}(x)=2x+3\),求方程 \(f^{'}(x)=2x+3=0\),得 x=-1.5,检查 \(f^{'}(x)=2x+3\) 在 -1.5 左右的正负号,当 x>-1.5 时,\(f^{'}(x)>0\),当 x<-1.5 时,\(f^{'}(x)<0\),可知 f(x) 在 -1.5 处取得极小值。从图上也可看出 f(x) 在 -1.5 处为最小值。
现在使用一维梯度下降算法来求 f(x) 的最小值。
deltaf = lambda x: x*2+3 # 定义 f 的导数
xk = 10 # 初始值
lamda = 0.01 # 步长
epsilon = 0.000001 # 精度
print Gradientdescent(f, xk, lamda, deltaf, epsilon)-1.49508514277计算结果与真实值 -1.5 差不多。