阿团团

《SICP》习题第2章

本人做的SICP习题第2章，如有错误请指正，用的解释器是Racket

练习2.1

;; Exercise 2.1
;; 有理数
#lang racket

;; 有理数定义
(define (numer x) (car x))
(define (demon x) (cdr x))
;; 处理分子分母均为正的有理数
(define (make-positive-rat n d)
  (let ((g (gcd n d)))
    (cons (/ n g) (/ d g))))
;; 处理正负有理数
(define (make-rat n d)
  (define positive-rat (make-positive-rat (abs n) (abs d)))
  (if (< (* n d) 0)
      (cons (- (numer positive-rat)) (demon positive-rat))
      positive-rat))

练习2.2

point相关的代码

;; Exercise 2.2
;; point
#lang racket
(provide (all-defined-out))

;; selector
(define (x-point x) (car x))
(define (y-point x) (cdr x))

;; make
(define (make-point x y) (cons x y))

;; print
(define (print-point p)
  (newline)
  (display "(")
  (display (x-point p))
  (display ",")
  (display (y-point p))
  (display ")"))

segment相关

;; Exercise 2.2
;; segment
#lang racket
(require "point.rkt")
(provide (all-defined-out))

;; selector
(define (start-segment x) (car x))
(define (end-segment x) (cdr x))

;; make
(define (make-segment start end)
  (cons start end))

;; 平均数
(define (avg x y)
  (/ (+ x y) 2.0))

;; 求中点
(define (midpoint-segment s)
  (make-point (avg (x-point (start-segment s)) (x-point (end-segment s))) (avg (y-point(start-segment s)) (y-point (end-segment s)))))

练习2.3

看起来题目是想让我们用多种不同的底层方法实现矩形，然后计算周长和面积的函数不论底层实现怎么样都可以用

先写周长和面积函数

;; Exercise 2.3
;; 矩形的相关计算
#lang racket
(require "rectangle-by-segment.rkt")
(provide (all-defined-out))

;; 计算周长
(define (perimeter rectangle)
  (* 2 (+ (width rectangle) (height rectangle))))

;; 计算面积
(define (area rectangle)
  (* (width rectangle) (height rectangle)))

第一种实现方法，用两根线定义矩形，为了方便计算长宽，修改练习2.2中的segment，增加一个函数计算线段的长度

;; 求线段长度
(define (length s)
  (sqrt (+ (square (- (x-point (start-segment s)) (x-point (end-segment s))))
           (square (- (y-point (start-segment s)) (y-point (end-segment s)))))))

现在实现矩形

;; Exercise 2.3
;; 通过宽和高定义矩形
#lang racket
(provide (all-defined-out))
(require "segment.rkt")

;; make
(define (make-rectangle s1 s2) (cons s1 s2))

;; selector
(define (width r)
  (length (car r)))
(define (height r)
  (length (cdr r)))

第二种方法，用四个点实现矩形，其实三个点就可以定义一个矩形，为了方便还规定了四个点必须按顺时针顺序输入（不然还要判断哪两个点在对角线上，麻烦）

;; Exercise 2.3
;; 通过4个点定义矩形
#lang racket
(require "point.rkt")
(require "segment.rkt")
(provide (all-defined-out))

;; make
(define (make-rectangle p1 p2 p3 p4)
  (cons (cons p1 p2) (cons p3 p4)))

;; selector
(define (width r)
  (length (make-segment (car (car r)) (cdr (car r)))))
(define (height r)
  (length (make-segment (cdr (car r)) (cdr (cdr r)))))

最后来写一个测试方法，测试两种矩形实现方式

;; Exercise 2.3
;; 矩形测试
#lang racket
(require "point.rkt")
(require "segment.rkt")
(require "rectangle-calculate.rkt")
;; 可以替换矩形底层实现
(require "rectangle-by-point.rkt")
;; (require "rectangle-by-segment.rkt")

;; 定义四个点
(define p1 (make-point 3 4))
(define p2 (make-point 5 6))
(define p3 (make-point 7 4))
(define p4 (make-point 5 2))

;; 定义两条边
(define s1 (make-segment p1 p2))
(define s2 (make-segment p2 p3))

;; 定义矩形
(define r (make-rectangle p1 p2 p3 p4))
;; (define r (make-rectangle s1 s2))

;; 计算周长和面积
(perimeter r)
(area r)

练习2.4

;; Exercise 2.4
;; cons的另一种定义方法
#lang racket

;; cons
(define (cons x y)
  (lambda (m) (m x y)))

;; selector
(define (car z)
  (z (lambda (p q) p)))
(define (cdr z)
  (z (lambda (p q) q)))

这段代码，(car (cons x y))可以替换为((lambda (m) (m x y)) (lambda (p q) p))

进一步替换为((lambda (p q) p) x y)

所以(car (cons x y))可以返回x

其实cons就是返回一个匿名函数，这个匿名函数接收一个函数，并将x、y作为参数输入给这个函数

练习2.5

;; Exercise 2.5
;; 用2^a3^b这个整数，记录a、b
#lang racket

;; cons
(define (cons a b)
  (* (expt 2 a) (expt 3 b)))

;; 判断是否为偶数
(define (even? x)
  (=  (remainder x 2) 0))

;; 获取x中因子a的个数
(define (get-factor-num x a)
  (define (iter n r)
    (if (= (remainder r a) 0)
        (iter (+ n 1) (/ r a))
        n))
  (iter 0 x))
      
;; selector
(define (car c)
  (get-factor-num c 2))
(define (cdr c)
  (get-factor-num c 3))

练习2.6

这道题的题干初看有点懵逼的，我个人肤浅的理解写在了这里SICP习题2.6 题目理解

求1，1就是(add-1 zero)，2就是(add-1 one)，以此类推，答案在下面，展开就是了

;; Exercise 2.6
;; 丘奇数
#lang racket

;; 0
(define zero (lambda (f) (lambda (x) x)))

;; 加1
(define (add-1 n)
  (lambda (f) (lambda (x) (f ((n f) x)))))

;; 1
(define one
  (lambda (f) (lambda (x) (f x))))

;; 2
(define two
  (lambda (f) (lambda (x) (f (f x)))))

总结一下，丘奇数，就是f(f(f(...x)))中，调用f的次数来表示对应的数的

仔细看一下丘奇数的函数，(丘奇数 f)这个调用所返回的函数就是给输入套上多层f的外壳，丘奇数对应几就套几个f壳

所以加法就是一个套壳的操作，两个输入是m和n（注意是丘奇数不是阿拉伯数字），先套n个壳，再套m个壳，就是加法了

;; 加
(define (add m n)
  (lambda (f)
    (lambda (x)
      ((m f) ((n f) x)))))

练习2.7

超简单

;; Exercise 2.7
;; 区间计算
#lang racket

;; make
(define (make-interval a b) (cons a b))

;; selector
(define (lower-bound i)
  (car i))
(define (upper-bound i)
  (cdr i))

练习2.8

;; 减
(define (sub-interval x y)
  (make-interval (- (lower-bound x) (upper-bound y))
                 (- (upper-bound y) (lower-bound y))))

练习2.9

假设区间和

对于加法，

区间的宽度为 $\frac{x_2+y_2-x_1-y_1}{2} = \frac{x_2-x_1}{2}+\frac{y_2-y_1}{2}$ ，等于原区间宽度之和

对于减法，

区间的宽度为 $\frac{x_2-y_2-x_1+y_1}{2} = \frac{x_2-x_1}{2}-\frac{y_2-y_1}{2}$ ，等于原区间宽度之差

对于乘法，假设有区间和，相乘得到，宽度为5，原宽度是1和3，并不等于原区间宽度的积

对于除法，假设有区间和，相除得到，宽度为5.5，原宽度是1和3，并不等于原区间宽度的商

练习2.10

;; 除
(define (div-interval x y)
  (if (span-zero? y)
      (error "the interval spans zero")
      (mul-interval x 
                    (make-interval (/ 1.0 (upper-bound y))
                                   (/ 1.0 (lower-bound y))))))

;; 检测区间是否跨过0，包含端点在0的情况
(define (span-zero? i)
  (and (<= (lower-bound i) 0) (>= (upper-bound i) 0)))

;; 检测区间是否跨过0，包含端点在0的情况
(define (span-zero? i)
  (and (<= (lower-bound i) 0) (>= (upper-bound i) 0)))

练习2.11

一个区间有9种情况，在0的左侧，在0的右侧，横跨0

因此两个区间就有9种情况，列个表，假设区间和，区间在0左侧就用<0表示，在0右侧表示为>0

分布情况	乘法
x>0,y>0
x>0,y=0
x>0,y<0
x=0,y>0
x=0,y=0
x=0,y<0
x<0,y>0
x<0,y=0
x<0,y<0

代码如下

;; 判断区间是否在0右侧
(define (right-zero? i)
  (and (> (lower-bound i) 0) (> (upper-bound i) 0)))

;; 乘
(define (mul-interval x y)
  (let ((p1 (* (lower-bound x) (lower-bound y)))
        (p2 (* (lower-bound x) (upper-bound y)))
        (p3 (* (upper-bound x) (lower-bound y)))
        (p4 (* (upper-bound x) (upper-bound y))))
    (cond ((right-zero? x)
           (cond ((right-zero? y) (make-interval p1 p4))
                 ((span-zero? y)  (make-interval p3 p4))
                 (else (make-interval p3 p2))))
          ((span-zero? x)
           (cond ((right-zero? y) (make-interval p2 p4))
                 ((span-zero? y)  (make-interval (min p2 p3) (max p1 p4)))
                 (else (make-interval p3 p1))))
          (else
           (cond ((right-zero? y) (make-interval p2 p3))
                 ((span-zero? y)  (make-interval p2 p1))
                 (else (make-interval p4 p1)))))))

练习2.12

;; 百分比表示，make
(define (make-center-percent c p)
  (make-interval (- c (* c p)) (+ c (* c p))))

;; 百分比表示，selector
(define (center i)
  (/ (+ (lower-bound i) (upper-bound i)) 2))
(define (percent i)
  (/ (- (upper-bound i) (center i)) (center i)))

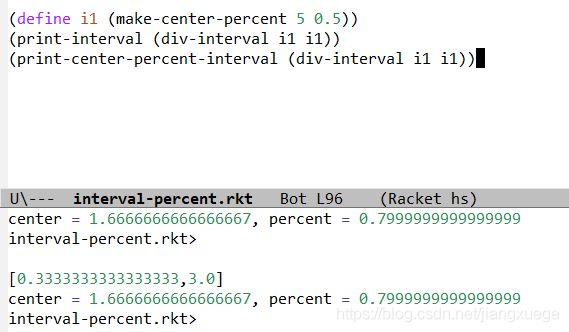
练习2.13

假设两个区间， $x_c\pm x_cx_p$ 和 $y_c\pm y_cy_p$ ，相乘得到的区间为

用百分比来表达，中心点为，误差百分比是是 $\frac{x_p+y_p}{1+x_py_p}$

练习2.14

现有的代码，A/A得不到[1,1]

练习2.15

par2可以得到正确的结果，par1是错误的

举个例子，两个电阻的阻值范围[2,3],[4,5]

par1计算的分子是[6,8]，分母是[8,15]

除出来是[0.6000000000000001,1.0]，是错误的，因为分子的最大值，8，是阻值取3和5的结果，而分母的最小值8，是阻值取2和4的结果

虽然电阻存在误差，但是一个电阻的阻值是不会变的，所以par1计算的是不可能存在的结果

学术一点来说，就是每个区间之间是独立的，但是出现在一个公式里的相同区间不是独立的，而我们程序考虑的都是每个输入区间完全独立的情况

如果每个区间只在计算中出现一次，就避免了这种情景，所以Eva Lu Ator说的是对的

练习2.16

思考了一下，区间运算，本质就是一个熟悉的数学问题，给出一个函数和多个自变量的范围，求函数的取值范围

如果自变量只有一个，很好做，初中都学过，如果自变量有多个呢，驻点、求偏导等一系列操作

首先，要写出正确的程序，我们必须时刻关注，出现一次以上的区间的相关性，需要把相同的区间区分开来

其次，要求偏导，求驻点，求偏导需要符号计算，求驻点需要解方程……

我感觉我这个水平做不到

练习2.17

;; Exercise 2.17
;; list
#lang racket

;; 返回list最后一个元素
(define (last-pair l)
  (if (null? (cdr l))
      (car l)
      (last-pair (cdr l))))

练习2.18

;; 反转list
(define (reverse l)
  (define (reverse-iter remain result)
    (if (null? remain)
        result
        (reverse-iter (cdr remain) (cons (car remain) result))))
  (reverse-iter l null))

练习2.19

;; Exercise 2.19
;; 使用list重写count-change
#lang racket

;; 硬币大小
(define us-coins (list 50 25 10 5 1))
(define uk-coins (list 100 50 20 10 5 2 1 0.5))

;; 计算找零方式
(define (cc amount coin-values)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (no-more? coin-values)) 0)
        (else
         (+ (cc amount
                (except-first-denomination coin-values))
            (cc (- amount
                   (first-denomination coin-values))
                coin-values)))))

;; 判断是否没有其余硬币作为选择
(define (no-more? coin-values)
  (null? coin-values))

;; 放弃使用当前硬币
(define (except-first-denomination coin-values)
  (cdr coin-values))

;; 获取当前硬币价值
(define (first-denomination coin-values)
  (car coin-values))

练习2.20

构建一个新的list，把符合条件的元素加到list里，最后反转整个list得到

;; Exercise 2.20
;; 返回与第一个元素奇偶性一致的元素
#lang racket
(require "list.rkt")

;; 判断奇偶性一致
(define (same? x y)
  (= (remainder x 2) (remainder y 2)))

;; 过滤
(define (same-parity x . l)
  (define (same-parity-iter remain result)
    (if (null? remain)
        (cons x (reverse result))
        (if (same? x (car remain))
            (same-parity-iter (cdr remain) (cons (car remain) result))
            (same-parity-iter (cdr remain) result))))
  (same-parity-iter l null))

练习2.21

;; 对队列中的每个数取平方，递归版
(define (square-list-recursive items)
  (if (null? items)
      null
      (cons (* (car items) (car items)) (square-list-recursive (cdr items)))))

;; 对队列中的每个数取平方，map版
(define (square-list-map items)
  (map (lambda(x) (* x x)) items))

练习2.22

越先和result进行cons操作的元素，越排在列表的后面

迭代的时候是从头到尾迭代的，所以最后的结果是反的

第二段代码是错误的，假设一个list是(1,2,3,4,5)

第一次迭代时，调用了(iter (1,2,3,4,5) nil)，最后执行了(cons null 1)

第二次迭代时，调用了(iter (2,3,4,5) (cons null 1)，最后执行了(cons (cons null 1) 4))

所以这段代码调用的结果是(((((() . 1) . 4) . 9) . 16) . 25)，这个结构不是list，是list结构的颠倒，如果把car和cdr调换一下，本质上还是一个(25,16,9,4,1)

练习2.23

;; Exercise 2.23
;; for循环
#lang racket

;; 对l中的每个元素执行f
(define (for-each f l)
  (cond ((not (null? l))
         (f (car l))
         (for-each f (cdr l)))))

练习2.24

eval之后是(1 (2 (3 4)))

练习2.25

比较难的就是第三个，对l3执行一次cdr之后得到的是一个list，但不是直接(2,3,4,5,6,7)，而是一个((2,3,4,5,6,7), null)，所以要一个car取出list

;; Exercise 2.25
;; 获取list中的7
#lang racket

(define l1 (list 1 3 (list 5 7) 9))
(define l2 (list (list 7)))
(define l3 (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7)))))))

;; 获取7
(car (cdr (car (cdr (cdr l1)))))
(car (car l2))
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr l3))))))))))))

练习2.26

答案分别是：

(1 2 3 4 5 6)
((1 2 3) 4 5 6)
((1 2 3) (4 5 6))

这一章一直很疑惑，为什么(cons (list 1 2) (list 3 4))是((1 2) 3 4)

展开一下list，是(cons 1 (cons 2 nil))和(cons 3 (cons 4 nil))

所以展开(cons (list 1 2) (list 3 4))

(cons (cons 1 (cons 2 nil)) (cons 3 (cons 4 nil)))，打印出来是((1 2) 3 4)，从展开式可以看出来这是一个3元素的list，第1个元素是list，后两个元素是数字，因为缺少了一个nil

再展开一下(list (list 1 2) (list 3 4))

(cons (cons 1 (cons 2 nil)) (cons (cons 3 (cons 4 nil)) nil))，打印出来是((1 2) (3 4))，从展开式可以看出来这是一个2元素的list，每个元素都是一个list

练习2.27

;; Exercise 2.27
;; 深度翻转list
#lang racket

;; 深度翻转list
(define (deep-reverse l)
  (define (iter remain result)
    (if (null? remain)
        result
        (iter (cdr remain) (cons (deep-reverse (car remain)) result))))
  (if (pair? l)
      (iter l null)
      l))

练习2.28

;; Exercise 2.28
;; 从左到右，返回一棵树的所有叶节点
#lang racket

;; 返回叶节点
(define (fringe tree)
  (cond ((null? tree) null)
        ((pair? tree) (append (fringe (car tree)) (fringe (cdr tree))))
        (else (list tree))))

练习2.29

;; mobile selector
(define (left-branch m)
  (car m))
(define (right-branch m)
  (car (cdr m)))

;; branch selector
(define (branch-length m)
  (car m))
(define (branch-structure m)
  (car (cdr m)))

;; 判断branch是否包含mobile
(define (branch-contains-mobile b)
  (pair? (branch-structure b)))

;; 判断branch的总重
(define (total-weight-branch b)
  (cond ((null? b) 0)
        ((branch-contains-mobile b) (total-weight (branch-structure b)))
        (else (branch-structure b))))

;; mobile的总重
(define (total-weight m)
  (cond ((null? m) 0)
        ((pair? m) (+ (total-weight-branch (left-branch m))
                      (total-weight-branch (right-branch m))))
        (else m)))

;; 计算branch产生的力矩
(define (torque b)
  (* (branch-length b) (total-weight-branch b)))

;; 判断branch是否平衡
(define (balance-branch b)
  (if (branch-contains-mobile b)
      (balance (branch-structure b))
      true))

;; 判断mobile是否平衡
(define (balance m)
  (if (null? m)
      true
      (and (= (torque (left-branch m)) (torque (right-branch m)))
           (balance-branch (left-branch m))
           (balance-branch (right-branch m)))))

只需要修改selector即可

;; Exercise 2.29
;; 用cons构造mobile
#lang racket

;; make mobile
(define (make-mobile left right)
  (cons left right))

;; make branch
(define (make-branch length structure)
  (cons length structure))

;; mobile selector
(define (left-branch m)
  (car m))
(define (right-branch m)
  (cdr m))

练习2.30

;; Exercise 2.39
;; 对树里的所有元素取平方
#lang racket

;; 对树里所有元素取平方
(define (square-tree t)
  (cond ((null? t) null)
        ((pair? t) (cons (square-tree (car t)) (square-tree (cdr t))))
        (else (square t))))

;; 平方
(define (square x)
  (* x x))

练习2.31

;; Exercise 2.31
;; 对树里的所有元素采取某种操作
#lang racket

;; map
(define (tree-map proc t)
  (cond ((null? t) null)
        ((pair? t) (cons (tree-map proc (car t)) (tree-map proc (cdr t))))
        (else (proc t))))

(define t
  (list 1
       (list 2 (list 3 4) 5)
       (list 6 7)))

(tree-map (lambda (x) (* x x)) t)

练习2.32

把一个集合分成两部分，首元素和其余部分，那么这个集合的所有子集，也可以分为两个部分

一个部分是其余部分的子集，另一个部分是其余部分的子集再加上首元素

以(1 2 3)为例，分为1和(2 3)，其子集分为两个部分

(2 3)的子集() (3) (2) (2 3)

和(2 3)子集并入首元素1，(1) (1 3) (1 2) (1 2 3)

;; Exercise 2.32
;; 生成一个list的所有子list
#lang racket

;; 子list生成
(define (subsets s)
  (if (null? s)
      (list null)
      (let ((rest (subsets (cdr s))))
        (append rest (map (lambda (l) (cons (car s) l)) rest)))))

练习2.33

;; map-by-accumulate
(define (map-by-accumulate p sequence)
  (accumulate (lambda (x y) (cons (p x) y)) null sequence))

;; append-by-accumulate
(define (append-by-accumulate seq1 seq2)
  (accumulate cons seq2 seq1))

;; length-by-accumulate
(define (length-by-accumulate sequence)
  (accumulate (lambda(x y) (+ y 1)) 0 sequence))

练习2.34

;; polynomial-by-accumulate
(define (horner-eval x coefficient-sequence)
  (accumulate (lambda (this-coeff higher-terms) (+
                                                  (* higher-terms x)
                                                  this-coeff))
               0
               coefficient-sequence))

练习2.35

首先使用map函数处理tree，tree是一个嵌套的list，用map函数把每个嵌套的子树映射为子树叶节点数量

map函数里递归调用了count-leaves来处理子树

;; count-leaves-by-accumulate
(define (count-leaves t)
  (accumulate +
              0
              (map (lambda(x)
                     (cond ((null? x) 0)
                           ((pair? x) (count-leaves x))
                           (else 1)))
                   t)))

练习2.36

加入输入的list都是3元素的，就先把所有队列第一个元素提取出来，计算，然后和剩余的（剩下的2元素）做cons

这里有一个小问题，为什么一开始判断null用的是(car seqs)而不是seqs

因为到最后seqs是(() ())，这种list不是空的，所以要用(car seqs)判断

;; 若干个list的对应位累计
(define (accumulate-n op initial seqs)
  (if (null? (car seqs))
      null
      (cons (accumulate op initial (map (lambda(x)
                                          (car x))
                                        seqs))
            (accumulate-n op initial (map (lambda(x)
                                            (cdr x))
                                          seqs)))))

练习2.37

;; 矩阵向量乘
(define (matrix-*-vector m v)
  (map (lambda (x) (dot-product x v)) m))

;; 矩阵转置
(define (transpose mat)
  (accumulate-n cons null mat))

;; 矩阵乘矩阵
(define (matrix-*-matrix m n)
  (let ((cols (transpose n)))
    (map (lambda(x) (matrix-*-vector cols x)) m)))

练习2.38

第一组，答案分别是3/2和1/6

fold-right，也就是accumulate，看一下展开的过程，是1/(2/(3/1))

fold-left，展开是1/1/2/3

第二组，答案分别是list (1 list (2 list (3 (nil))))和(list (list (list nil 1) 2) 3)

跟上面类似，不展开了

跟执行顺序无关的符号，满足结合律，即算子（参数）位置没有改变，运算顺序（用括号改变）不会对结果有影响

比如加法，就可以在fold-right和fold-left取得相同结果

练习2.39

fold-right，利用append

;; 翻转
(define (reverse sequence)
  (fold-right (lambda(x y)
                (append y (list x)))
              null
              sequence))

fold-left的很好写

;; 翻转
(define (reverse sequence)
  (fold-left (lambda(x y) (cons y x)) null sequence))

练习2.40

;; 生成整数对，并过滤和不为质数的部分
(define (prime-sum-pairs n)
  (map make-pair-sum
       (filter prime-sum? (unique-pairs n))))

;; 产生1<= j< i<= n的整数对
(define (unique-pairs n)
  (flatmap
   (lambda (i)
     (map (lambda(j) (list i j))
          (enumerate-interval 1 (- i 1))))
   (enumerate-interval 1 n)))

练习2.41

和上面的类似，照着写就行了

;; 产生1<=k

 
    
  练习2.42 
  ;; Exercise 2.42
;; N皇后
#lang racket
(require "prime-sum-pairs.rkt")
(require "sequence-operations.rkt")

;; N皇后
;; 当前棋盘的可能状态用一组list表示，每个list表示一种皇后放置方法，每个list对应下标存放的数值表示这一列皇后放在哪一行
(define (queens board-size)
  (define (queen-cols k)  
    (if (= k 0)
        (list empty-board)
        (filter
         (lambda (positions) (safe? k positions))
         (flatmap
          (lambda (rest-of-queens)
            (map (lambda (new-row)
                   (adjoin-position new-row k rest-of-queens))
                 (enumerate-interval 1 board-size)))
          (queen-cols (- k 1))))))
  (queen-cols board-size))

;; 空棋盘
(define empty-board null)

;; 放入新的一列，new-row表示新放入的第k列皇后处于哪一行
(define (adjoin-position new-row k rest-of-queens)
  (cons new-row rest-of-queens))

;; 判断第k列的皇后位置是否合法
(define (safe? k positions)
  ;; 判断皇后所处行是否有重复，是否会在对角线碰撞
  (and (unique-first positions)
       ;; 判断皇后是否在对角线碰撞
       (not-crash? positions)))
       
;; 判断list中首元素是否是不重复
(define (unique-first l)
  (= (list-item-num l (car l)) 1))

;; 获取list中某个给定值出现了几次
(define (list-item-num l item)
  (length (filter (lambda(x) (= x item)) l)))

;; 判断新皇后是否会和其他皇后碰撞
(define (not-crash? l)
  ;; 沿着对角线逐步检查是否相撞
  ;; cur表示会与新皇后相撞的位置
  ;; direction为±1，表示两个对角线方向
  (define (check remain cur direction)
    (if (null? remain)
        #t
        (and (not (= (car remain) cur))
             (check (cdr remain) (+ cur direction) direction))))
  (and (check (cdr l) (+ (car l) 1) 1)
       (check (cdr l) (+ (car l) -1) -1))) 
  部分答案如下 
   
    
  练习2.43 
  原来的写法，每次做flatmap时，调用一次queen-cols，线形调用，耗费的时间是 
  现在这种写法，每次做flatmap时，调用board-size次queen-cols，变成了树形递归调用，根据前面的知识，树形递归调用耗费的时间是，随问题规模呈指数增长，常数与执行一次调用耗费时间有关，显然C大致为 
  所以更改后的代码，耗费时间大约为 
    
  练习2.4 
  ;; 在画作上方画两幅更小的画作
(define (up-split painter n)
  (if (= n 0)
      painter
      (let ((smaller (up-split painter (- n 1))))
        (below painter (beside smaller smaller))))) 
    
  练习2.45 
  ;; split，d1表示小画和大画的组合方式，d2表示两幅小画的组合方式
(define (split d1 d2)
  (lambda (painter n)
    (if (= n 0)
        painter
        (let ((smaller ((split d1 d2) painter (- n 1))))
          (d1 painter (d2 smaller smaller)))))) 
    
  练习2.46 
  没什么难度 
  ;; Exercise 2.46
;; 向量
#lang racket

;; make
(define (make-vect x y)
  (cons x y))

;; selector
(define (xcor-vect v)
  (car v))
(define (ycor-vect v)
  (cdr v))

;; 加
(define (add-vect v1 v2)
  (make-vect (+ (xcor-vect v1) (xcor-vect v2))
             (+ (ycor-vect v1) (ycor-vect v2))))

;; 减
(define (sub-vect v1 v2)
  (make-vect (- (xcor-vect v1) (xcor-vect v2))
             (- (ycor-vect v1) (ycor-vect v2))))

;; 乘系数
(define (scale-vect v s)
  (make-vect (* (xcor-vect v) s)
             (* (ycor-vect v) s)))
 
    
  练习2.47 
  第一种 
  ;; Exercise 2.47
;; frame
#lang racket

;; make
(define (make-frame origin edge1 edge2)
  (list origin edge1 edge2))

;; selector
(define (origin-frame f)
  (car f))
(define (edge1-frame f)
  (cadr f))
(define (edge2-frame f)
  (cadr (cdr f))) 
  第二种 
  ;; Exercise 2.47
;; frame
#lang racket

;; make
(define (make-frame origin edge1 edge2)
  (cons origin (cons edge1 edge2)))

;; selector
(define (origin-frame f)
  (car f))
(define (edge1-frame f)
  (cadr f))
(define (edge2-frame f)
  (cdr (cdr f))) 
    
  练习2.48 
  ;; Exercise 2.48
;; segment
#lang racket
(require "vector.rkt")
(provide (all-defined-out))

;; make
(define (make-segment v1 v2)
  (cons v1 v2))

;; selector
(define (start-segment s)
  (car s))
(define (end-segment s)
  (cdr s)) 
    
  练习2.49 
  a. 
  ;; 画出外框
(define (draw-outline frame)
  ;; 四个端点
  (let ((v1 (make-vect 0 1))
        (v2 (make-vect 0 0))
        (v3 (make-vect 1 0))
        (v4 (make-vect 1 1)))
    (segments->painter (list (make-segment v1 v2)
                             (make-segment v2 v3)
                             (make-segment v3 v4)
                             (make-segment v4 v1))))) 
  b. 
  ;; 画X
(define (draw-x frame)
  ;; 四个端点
  (let ((v1 (make-vect 0 1))
        (v2 (make-vect 0 0))
        (v3 (make-vect 1 0))
        (v4 (make-vect 1 1)))
    (segments->painter (list (make-segment v1 v3)
                             (make-segment v2 v4))))) 
  c. 
  ;; 画菱形
(define (draw-diamond frame)
  ;; 四个中点
  (let ((v1 (make-vect 0.0 0.5))
        (v2 (make-vect 0.5 1.0))
        (v3 (make-vect 1.0 0.5))
        (v4 (make-vect 0.5 0.0)))
    (segments->painter (list (make-segment v1 v2)
                             (make-segment v2 v3)
                             (make-segment v3 v4)
                             (make-segment v4 v1))))) 
  d. 
  我必须承认我是从网上抄的 
  ;; 画挥手的小人
(define wave-painter-segments
  (segments->painter
   (list (make-segment (make-vect 0.2 0.0) (make-vect 0.4 0.4))
         (make-segment (make-vect 0.4 0.4) (make-vect 0.3 0.5))
         (make-segment (make-vect 0.3 0.5) (make-vect 0.1 0.3))
         (make-segment (make-vect 0.1 0.3) (make-vect 0.0 0.6))
         (make-segment (make-vect 0.0 0.8) (make-vect 0.1 0.5))
         (make-segment (make-vect 0.1 0.5) (make-vect 0.3 0.6))
         (make-segment (make-vect 0.3 0.6) (make-vect 0.4 0.6))
         (make-segment (make-vect 0.4 0.6) (make-vect 0.3 0.8))
         (make-segment (make-vect 0.3 0.8) (make-vect 0.4 1.0))
         (make-segment (make-vect 0.6 1.0) (make-vect 0.7 0.8))
         (make-segment (make-vect 0.7 0.8) (make-vect 0.6 0.6))
         (make-segment (make-vect 0.6 0.6) (make-vect 0.8 0.6))
         (make-segment (make-vect 0.8 0.6) (make-vect 1.0 0.4))
         (make-segment (make-vect 1.0 0.2) (make-vect 0.6 0.4))
         (make-segment (make-vect 0.6 0.4) (make-vect 0.8 0.0))
         (make-segment (make-vect 0.7 0.0) (make-vect 0.5 0.3))
         (make-segment (make-vect 0.5 0.3) (make-vect 0.3 0.0))))) 
    
  练习2.50 
  ;; 水平翻转
(define (flip-horiz painter)
  ((transform-painter painter
                      (make-vect 1.0 0.0)
                      (make-vect 0.0 0.0)
                      (make-vect 1.0 1.0))
   painter))

;; 顺时针旋转180度
(define (rotate180 painter)
  ((transform-painter painter
                      (make-vect 1 1)
                      (make-vect 0 1)
                      (make-vect 1 0))
   painter))

;; 顺时针旋转270度
(define (rotate270 painter)
  ((transform-painter painter
                      (make-vect 0 1)
                      (make-vect 0 0)
                      (make-vect 1 1))
   painter)) 
    
  练习2.51 
  仿照beside的写法 
  ;; below
(define (below painter-bottom painter-top)
  (let ((paint-top
         (transform-painter painter-top
                            (make-vect 0.0 0.5)
                            (make-vect 1.0 0.5)
                            (make-vect 0.0 1.0)))
        (paint-below
         (transform-painter painter-bottom
                            (make-vect 0.0 0.0)
                            (make-vect 1.0 0.0)
                            (make-vect 0.0 0.5))))
    (lambda (frame)
      (paint-top frame)
      (paint-bottom frame))))
 
  如果用beside加rotate实现below 
  ;; beside实现below
(define (below-by-biside painter-bottom painter-top)
  (rotate270 (beside (rotate90 painter-bottom)
                      (rotate90 painter-up))))
 
    
  练习2.52 
  a. 
  给你画个对角线 
  ;; 画挥手的小人
(define wave-painter-segments
  (segments->painter
   (list (make-segment (make-vect 0.0 0.0) (make-vect 1.0 1.0))
         (make-segment (make-vect 0.2 0.0) (make-vect 0.4 0.4))
         (make-segment (make-vect 0.4 0.4) (make-vect 0.3 0.5))
         (make-segment (make-vect 0.3 0.5) (make-vect 0.1 0.3))
         (make-segment (make-vect 0.1 0.3) (make-vect 0.0 0.6))
         (make-segment (make-vect 0.0 0.8) (make-vect 0.1 0.5))
         (make-segment (make-vect 0.1 0.5) (make-vect 0.3 0.6))
         (make-segment (make-vect 0.3 0.6) (make-vect 0.4 0.6))
         (make-segment (make-vect 0.4 0.6) (make-vect 0.3 0.8))
         (make-segment (make-vect 0.3 0.8) (make-vect 0.4 1.0))
         (make-segment (make-vect 0.6 1.0) (make-vect 0.7 0.8))
         (make-segment (make-vect 0.7 0.8) (make-vect 0.6 0.6))
         (make-segment (make-vect 0.6 0.6) (make-vect 0.8 0.6))
         (make-segment (make-vect 0.8 0.6) (make-vect 1.0 0.4))
         (make-segment (make-vect 1.0 0.2) (make-vect 0.6 0.4))
         (make-segment (make-vect 0.6 0.4) (make-vect 0.8 0.0))
         (make-segment (make-vect 0.7 0.0) (make-vect 0.5 0.3))
         (make-segment (make-vect 0.5 0.3) (make-vect 0.3 0.0))))) 
  b. 
  ;; corner split
(define (corner-split painter n)
  (if (= n 0)
      painter
      (let ((up (up-split painter (- n 1)))
            (right (right-split painter (- n 1)))
            (corner (corner-split painter (- n 1))))
        (beside (below painter up)
                (below right corner))))) 
  c. 
  ;; square limit
(define (square-limit painter n)
  (let ((combine4 (square-of-four identity flip-horiz
                                  flip-vert rotate180)))
    (combine4 (corner-split painter n)))) 
    
  练习2.53 
  '(a b c)
 '((george))
 '((y1 y2))  后面还有一个nil，所以是一个list，里面包含(y1,y2)和nil
 '(y1 y2)
 #f
 #f  检查两个元素(red shoes)和(blue socks)，均不等于red
 '(red shoes blue socks) 
    
  练习2.54 
  ;; Exercise 2.54
;; 判断list是否相等
#lang racket

;; 判断两个list是否完全相等
(define (equal? l1 l2)
  (cond ((and (null? l1) (null? l2)) #t)
        ((or (null? l1) (null? l2) (not (eq? (car l1) (car l2)))) #f)
        (else (equal? (cdr l1) (cdr l2)))))
 
    
  练习2.55 
  (car ''abracadabra)，展开就是(car '(quote abracadabra)) 
    
  练习2.56 
  简单写了一个，仅支持指数为数字的形式 
  先写幂运算相关的make和selector 
  ;; 判断是否是求幂
(define (exp? x)
  (and (pair? x)
       (eq? (car x) '**)))

;; 求幂
(define (make-exp base exponent)
  (if (or (=number? base 1) (=number? exponent 0))
      1
      (list '** base exponent)))

;; 获取幂的基数、指数
(define (base e) (cadr e))
(define (exponent e) (caddr e)) 
  然后修改求导 
  ;; 求导
(define (deriv exp var)
  (cond ((number? exp) 0)
        ((variable? exp)
         (if (same-variable? exp var) 1 0))
        ((sum? exp)
         (make-sum (deriv (addend exp) var)
                   (deriv (augend exp) var)))
        ((product? exp)
         (make-sum (make-product (multiplier exp)
                                 (deriv (multiplicand exp) var))
                   (make-product (deriv (multiplier exp) var)
                                 (multiplicand exp))))
        ((exp? exp)
         (make-product (make-product (exponent exp)
                                     (make-exp (base exp) (- (exponent exp) 1)))
                       (deriv (base exp) var)))
        (else
         (error "unknwon expression type -- DERIV" exp)))) 
    
  练习2.57 
  只修改augend和multiplicand的定义，举个例子，addend还是保存第一项，augend保存之后的所有项的和 
  例如，(+ x y z)的addend是x，augend是(+ y z) 
  ;; 获取加数
(define (augend s)
  (let ((rest (cddr s)))
    (if (null? (cdr rest))
        (car rest)
        (cons '+ rest))))

;; 获取乘数
(define (multiplicand p)
  (let ((rest (cddr p)))
    (if (null? (cdr rest))
        (car rest)
        (cons '* rest)))) 
    
  练习2.58 
  a. 
  ;; 判断是否是求和式
(define (sum? x)
  (and (pair? x) (eq? (cadr x) '+)))

;; 判断是否是求积式
(define (product? x)
  (and (pair? x) (eq? (cadr x) '*)))

;; 获取加数
(define (addend s) (car s))
(define (augend s) (caddr s))

;; 获取乘数
(define (multiplier p) (car p))
(define (multiplicand p) (caddr p))

;; 求和
(define (make-sum a1 a2)
  (cond ((=number? a1 0) a2)
        ((=number? a2 0) a1)
        ((and (number? a1) (number? a2)) (+ a1 a2))
        (else (list a1 '+ a2))))

;; 求积
(define (make-product m1 m2)
  (cond ((or (=number? m1 0) (=number? m2 0)) 0)
        ((=number? m1 1) m2)
        ((=number? m2 1) m1)
        ((and (number? m1) (number? m2)) (* m1 m2))
        (else (list m1 '* m2)))) 
    
  b. 
  需要考虑的情况是，当加法前含有乘法运算时，如何准确地识别加法 
  例如，4 * x + x * x，需要判定为求和，并且拆分出4 * x和x * x，再对子项进行求导 
  那么只需要在判断表达式的死后，当表达式含有+，就判定为加法，先行进行处理 
  ;; 判断是否是求和式
(define (sum? x)
  (contains? x '+))

;; 判断是否是求积式
(define (product? x)
  (and (not (contains? x '+)) (contains? x '*)))

;; 判断list中是否含有某元素
(define (contains? l item)
  (cond ((null? l) #f)
        ((eq? (car l) item) #t)
        (else (contains? (cdr l) item)))) 
  乘法的selector修改成类似习题2.57中的样子（但需要修改，注意*号的位置，不是最前面而是中间），以支持多项计算，加法的selector需要在“+”处切分 
  ;; 从list中获取指定item之前的部分
(define (get-before l item)
  (define (iter remain)
    (if (or (null? remain) (eq? (car remain) item))
        null
        (cons (car remain) (iter (cdr remain)))))
  (remove-brackets-if-only-one (iter l)))

;; 从list中获取指定item之后的部分
(define (get-after l item)
  (define (iter remain)
    (cond ((null? remain) null)
          ((eq? (car remain) item) (cdr remain))
          (else (iter (cdr remain)))))
  (remove-brackets-if-only-one (iter l)))

;; 若list中只含有一个元素，去除括号
(define (remove-brackets-if-only-one l)
  (if (null? (cdr l))
      (car l)
      l))

;; 获取加数
(define (addend s) (get-before s '+))
(define (augend s) (get-after s '+))

;; 获取乘数
(define (multiplier p) (car p))
(define (multiplicand p)
  (let ((rest (cddr p)))
    (if (null? (cdr rest))
        (car rest)
        rest)))
 
    
  练习2.59 
  ;; 取并集
(define (union-set set1 set2)
  (cond ((or (null? set1) (null? set2)) set2)
        ((element-of-set? (car set1) set2)
         (union-set (cdr set1) set2))
        (else (cons (car set1) (union-set (cdr set1) set2))))) 
    
  练习2.60 
  由可重复列表构成的集合，代码如下 
  ;; Exercise 2.60
;; 允许重复的列表构成的集合
#lang racket

;; 判断集合是否包含某个元素
(define (element-of-set? x set)
  (cond ((null? set) false)
        ((equal? x (car set)) true)
        (else (element-of-set? x (cdr set)))))

;; 在集合中加入元素
(define (adjoin-set x set)
  (cons x set))

;; 取交集 
(define (union-set set1 set2)
  (cond ((null? set1) set2)
        ((null? set2) set1)
        (else (union-set (cdr set1) (cons (car set1) set2)))))

;; 取并集
(define (intersection-set set1 set2)
  (cond ((or (null? set1) (null? set2)) null)
        ((element-of-set? (car set1) set2)
         (cons (car set1)
               (intersection-set (cdr set1) set2)))
        (else (intersection-set (cdr set1) set2)))) 
  和由不可重复列表构成集合的各项操作复杂度对比 
   
    
     
     分类 
     element-of-set? 
     adjoin-set 
     union-set 
     intersection-set 
     
     
     重复列表 
      
      
      
      
     
     
     不可重复列表 
      
      
      
      
     
    
   
  虽然有部分操作复杂度降低了，但是带来的是更大的存储开销，在数据重复度很高的情况下，重复列表的长度会比不重复列表大很多，操作也会变慢，因此需要根据应用来选择合适的底层实现方式 
    
  练习2.61 
  ;; Exercise 2.61
;; 有序列表构成的集合
#lang racket

;; 向集合增加元素
(define (adjoin-set x set1)
  (cond ((null? set1) (cons x null))
        ((= (car set1) x) set1)
        ((> (car set1) x) (cons x set1))
        (else (cons (car set1) (adjoin-set x (cdr set1)))))) 
    
  练习2.62 
  ;; 取交集
(define (union-set set1 set2)
  (cond ((null? set1) set2)
        ((null? set2) set1)
        (else
         (let ((x1 (car set1))
               (x2 (car set2)))
           (cond ((= x1 x2) (cons x1 (union-set (cdr set1) (cdr set2))))
                 ((< x1 x2) (cons x1 (union-set (cdr set1) set2)))
                 (else (cons x2 (union-set set1 (cdr set2))))))))) 
    
  练习2.63 
  a. 
  两种写法都一样，是前序遍历 
  对于图2.16，结果都是1 3 5 7 9 11 
  b. 
  两种写法的递归调用次数都是差不多的，那么就比较每一次的操作 
  第一种写法使用了append操作，比第二种写法的cons操作，显然复杂度更高 
    
  练习2.64 
  a. 
  非常多的let嵌套简直惊悚，建议从下往上看，清晰很多 
  首先partial-tree有两个输入，一个是元素列表，一个是元素列表长度 
  partial-tree的返回是一个pair，从最后一行可以猜出，pair是已经组合好的树和未处理的元素 
  再读一读let嵌套就可以知道，partial-tree先把左子树的所有元素处理成树，返回未处理的元素（包含entry和右子树的所有元素），然后依次处理entry和右子树 
  处理的结果是(5 (1 () (3 () ())) (9 (7 () ()) (11 () ()))) 
  对每个元素都处理依次，因此复杂度为 
  b. 
  首先把二叉树转换成list，再按照需求进行交或并的归并，再把处理好的list转换成二叉树 
  三种操作的复杂度都是 
  ;; 取交集
(define (union-set set1 set2)
  (let ((list1 (tree->list-1 set1))
        (list2 (tree->list-1 set2)))
    ;; 取两个有序列表交集
    (define (merge list1 list2)
      (cond ((null? list1) list2)
            ((null? list2) list1)
            (else
             (let ((x1 (car list1))
                   (x2 (car list2)))
               (cond ((= x1 x2) (cons x1 (merge (cdr list1) (cdr list2))))
                     ((< x1 x2) (cons x1 (merge (cdr list1) list2)))
                     (else (cons x2 (merge list1 (cdr list2)))))))))
    (let ((union-list (merge list1 list2)))
      (list->tree union-list))))

;; 取交集
(define (intersection-set set1 set2)
  (let ((list1 (tree->list-1 set1))
        (list2 (tree->list-2 set2)))
    ;; 取两个有序列表并集
    (define (merge list1 list2)
      (if (or (null? list1) (null? list2))
          null
          (let ((x1 (car list1))
                (x2 (car list2)))
            (cond ((= x1 x2) (cons x1 (merge (cdr list1) (cdr list2))))
                  ((< x1 x2) (merge (cdr list1) list2))
                  (else (merge list1 (cdr list2)))))))
    (let ((intersection-list (merge list1 list2)))
      (list->tree intersection-list)))) 
    
  练习2.66 
  ;; 查找
(define (lookup set1 key)
  (if (null? set1)
      false
      (let ((x (entry set1)))
        (cond ((= x key) true)
              ((< x key) (lookup (right-branch set1) key))
              (else (lookup (left-branch set1) key)))))) 
    
  练习2.67 
  A D A B B C A 
    
  练习2.68 
  ;; 编码
(define (encode message tree)
  (if (null? message)
      '()
      (append (encode-symbol (car message) tree)
              (encode (cdr message) tree))))

;; 编码一个symbol
(define (encode-symbol symbol tree)
  ;; 判断有序集合中是否含有某元素
  (define (contains? set1 s)
    (cond ((null? set1) false)
          ((equal? (car set1) s) true)
          (else (contains? (cdr set1) s))))
  ;; 判断子树是否包含symbol
  (define (tree-contains? s t)
    (contains? (symbols t) s))
  (cond ((leaf? tree) null)
        ((tree-contains? symbol (left-branch tree))
         (cons 0 (encode-symbol symbol (left-branch tree))))
        ((tree-contains? symbol (right-branch tree))
         (cons 1 (encode-symbol symbol (right-branch tree))))
        (else (error ("待加密信息输入错误")))))
         
;; 测试编码      
(define sample-characters '(A D A B B C A))
(encode sample-characters sample-tree) 
    
  练习2.69 
  ;; 将最小的元素合并为一个节点
(define (successive-merge ordered-pairs)
  (if (= (length ordered-pairs) 1)
      (car ordered-pairs)
      (let ((leaf1 (car ordered-pairs))
            (leaf2 (cadr ordered-pairs))
            (remains (cddr ordered-pairs)))
        (successive-merge (adjoin-set (make-code-tree leaf1 leaf2) remains))))) 
    
  练习2.70 
  利用霍夫曼编码，只要84位bit，定长3-bit编码需要108位 
    
  练习2.71 
  对于这种频率，在合并树节点的时候，两个最小的节点合并后仍然是最小的节点，n=5的时候霍夫曼树如下 
   
  因此这种情况，频率最高的节点，霍夫曼编码是1位，频率最低的节点，霍夫曼编码是n-1位 
    
  练习2.72 
  对一个长度为n的message，假设单词为m个，调用n次encode函数，每个encode函数调用一次encode-symbol 
  一次encode-symbol，每次都要在节点的set中搜寻symbol是否存在，然后沿着节点一次向下搜寻沿着节点，所以复杂度和霍夫曼树是否平衡有关。在不知道霍夫曼树结构的情况下，计算复杂度是很困难的 
  以练习2.71中的霍夫曼树为例 
  对于最频繁出现的symbol，在第一个节点set中搜寻即可找到，第一个节点set长度为n，所以复杂度是 
  对于最不频繁出现的symbol，要在(n-1)个节点的set中搜寻，每个set的长度与n成正比，所以复杂度是 
    
  练习2.73 
  a. 
  数据导向的求导程序 
  因为数字和符号已经有了内置的number?、variable?这种函数，如果对数字、变量也打数据标签，要多很多操作 
  b. 
  先把给数据打标签的代码写好 
  ;; 带标签数据
#lang racket
(provide (all-defined-out))

;; 给数据打标签
(define (attach-tag type-tag contents)
  (cons type-tag contents))

;; 获取数据标签
(define (type-tag datum)
  (if (pair? datum)
      (car datum)
      (error "Bad tagged datum -- TYPE-TAG" datum)))

;; 获取数据内容
(define (contents datum)
  (if (pair? datum)
      (cdr datum)
      (error "Bad tagged datum -- CONTENTS" datum))) 
  sum和product的install代码 
  ;; sum数据类型
(define (install-sum-package)
  ;; 内部函数
  ;; 构造函数
  (define (make-sum x y)
    (cond ((=number? x 0) y)
          ((=number? y 0) x)
          ((and (number? x) (number? y)) (+ x y))
          (else (attach-tag '+ x y))))
  ;; 获取第一个加数
  (define (addend s)
    (car s))
  ;; 获取第二个加数
  (define (augend s)
    (cadr s))
  ;; 求导
  (define (diff-sum operands var)
    (make-sum (deriv (addend operands) var)
              (deriv (augend operands) var)))
  ;; 注册函数
  (put 'deriv '+ diff-sum))
  (put 'make  '+ make-sum))

;; product数据类型
(define (install-product-package)
  ;; 内部函数
  ;; 构造函数
  (define (make-product x y)
    (cond ((=number? x 1) y)
          ((=number? y 1) x)
          ((or (=number? x 0) (=number? y 0)) 0)
          ((and (number? x) (number? y)) (+ x y))
          (else (attach-tag '* x y))))
  ;; 获取第一个乘数
  (define (multiplier s)
    (car s))
  ;; 获取第二个乘数
  (define (multiplicand s)
    (cadr s))
  ;; 求导
  (define (diff-product operands var)
    (make-sum (make-product
               (multiplier operands)
               (deriv (multiplicand operands) var))
              (make-product
               (deriv (multiplier operands) var)
               (multiplicand operands))))
  ;; 接口
  (put 'deriv '* diff-product)
  (put 'make  '* make-product))

(define make-sum (get 'make '+))
(define make-product (get 'make '*)) 
  c. 
  ;; 指数数据类型
(define (install-exp-package)
  ;; 内部函数
  ;; 构造函数
  (define (make-exp x y)
    (cond ((=number? y 0) 1)
          ((=number? y 1) x)
          ((and (number? x) (number? y)) (** x y))
          (else (attach-tag '** x y))))
  ;; 获取基数
  (define (base s)
    (car s))
  ;; 获取指数
  (define (exponent s)
    (cadr s))
  ;; 求导
  (define (diff-exp operands var)
    (let ((b (base operands))
          (e (exponent operands)))
      (make-product e
                    (make-product (deriv e var)
                                  (make-exp b (make-sum e -1)))))
  ;; 接口
  (put 'deriv '** diff-exp)
  (put 'make  '** make-exp)) 
  d. 
  把所有put操作的前两个参数调换位置就可以了 
    
  2.74 
  由题意，每个独立文件以不同的数据结构存放员工信息，以员工姓名为主键 
  a. 
  每个文件的数据都分配一个tag，都公开以下接口： 
   
   通过员工姓名查询员工信息记录的get函数 
   各种select函数，包括薪水、入职日期等 
   
  get_record函数通过员工姓名在文件中查询员工信息，在不同文件中查询时，只要根据不同的数据tag选择对应的get函数就可以了 
  b. 
  通过每条员工信息的数据tag，选择对应的select函数，查询薪水 
  c. 
  在不同文件中搜索，直到搜索到该姓名为止 
  d. 
  分配给新公司一个tag，并在它原来的员工数据基础上，增加对应的get和select函数 
    
  2.75 
  这个message写起来比tag简单多了 
  伟大的面向对象思想 
  ;; 极坐标
(define (make-from-mag-ang m a)
  (define (dispatch op)
    (cond ((eq? op 'magnitude) m)
          ((eq? op 'angle) a)
          ((eq? op 'real-part) (* m (cos a)))
          ((eq? op 'imag-part) (* m (sin a)))
          (else
           (error "Unknown op -- MAKE-FROM-MAG-ANG" op))))
  dispatch) 
    
  2.76 
  显式分派：非常麻烦，每个类型的每个方法名字要注意区分，大型系统中简直是噩梦的存在 
  tag：增加类型，要分配一个新tag，并更新全局函数表；增加方法要更新全局函数表；之前的代码无需修改 
  message：增加类型几乎不需要额外的开销；增加方法，其实和tag相比要加入的代码量是类似的，但是tag法的方法代码可以不和同类代码放在一起，message的方法必须和类写在一个dispatch函数里，所以tag法增加方法更加地方便一些（写起来方便，写的量我觉得差不多） 
  综上，经常增加类，使用message法，经常增加方法，使用tag法 
    
  练习2.77 
  magnitude只在install函数内部定义了，其他函数无法直接调用install函数内部定义的函数 
    
  练习2.78 
  加个判断分支就好，number和symbol不打tag，获取标签的时候，判断为number?或symbol?的直接返回对应tag 
  ;; Exercise 2.78
;; 带标签数据，可处理系统自带number和symbol
#lang racket

;; 给数据打标签
(define (attach-tag type-tag contents)
  (cons type-tag contents))

;; 获取数据标签
(define (type-tag datum)
  (cond ((number? datum) 'number)
        ((symbol? datum) 'symbol)
        ((pair? datum) (car datum))
        (else (error "Bad tagged datum -- TYPE-TAG" datum))))

;; 获取数据内容
(define (contents datum)
  (cond ((or (number? datum) (symbol? datum)) datum)
        ((pair? datum) (cdr datum))
        (else (error "Bad tagged datum -- CONTENTS" datum)))) 
    
  练习2.79 
  写数字包 
  ;; 数字包
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "install-rational-package.rkt")
(provide (all-defined-out))

;; 数字包
(define (install-scheme-number-package)
  (define (tag x)
    (attach-tag 'scheme-number x))
  ;; 判断数字是否为0
  (define (number-zero? n)
    (= n 0))
  (put 'add '(scheme-number scheme-number)
       (lambda (x y) (tag (+ x y))))
  (put 'sub '(scheme-number scheme-number)
       (lambda (x y) (tag (- x y))))
  (put 'mul '(scheme-number scheme-number)
       (lambda (x y) (tag (* x y))))
  (put 'div '(scheme-number scheme-number)
       (lambda (x y) (tag (/ x y))))
  (put 'make 'scheme-number
       (lambda (x) (tag x)))
  ;; 判断数字是否相等
  (put 'equ? '(scheme-number scheme-number) =)
  'done)

;; 构造函数
(define (make-scheme-number x)
  ((get 'make 'scheme-number) x))
 
  有理数判断是否相等 
  ;; 判断有理数是否相等
(define (rational-eq? r1 r2)
  (= (* (numer r1) (denom r2))
     (* (denom r1) (numer r2))))
(put 'equ? 'rational rational-eq?) 
  复数判断是否相等 
  ;; 判断复数是否相等
(define (equ? z1 z2)
  (and (= (real-part z1) (real-part z2)) (= (imag-part z1) (imag-part z2))))
(put 'equ? '(complex complex) equ?) 
  练习2.80 
  类似操作 
  ;; Exercise 2.80
;; 泛型数字操作
#lang racket

;; 判断有理数是否为零
(define (rational-zero? r)
  (= (numer r) 0))
(put 'zero? 'rational rational-zero?)

;; 判断复数是否为零
(define (complex-zero? c)
  (and (= (real-part c) 0) (= (imag-part c) 0)))
(put 'zero? 'complex complex-zero?)

;; 判断数字是否为0
(define (number-zero? n)
  (= n 0))
(put 'zero? 'number number-zero?) 
    
  练习2.81 
  a. 
  apply-generic函数有两个分支：一个分支是找到当前输入类型对应的操作函数，调用函数，完成操作；或者尝试输入数据的类型转换，再用新输入类型调用apply-generic 
  如果加上scheme-number自身的转换，(apply-generic scheme-number scheme-number)会重复a1->a2类型转换，然后调用(apply-generic scheme-number scheme-number)，程序陷入死循环 
  b. 
  从上一小题分析可以看出来，apply-generic首先查找是否有对应输入类型的操作函数，查找不到就会尝试进行类型转换；如果加入同类型转换的函数，转换前后没有任何改变，找不到操作函数还是找不到，必然会引起死循环调用 
  c. 
  要运行这个函数，要自己模拟一下get-coercion函数 
  ;; Exercise 2.81
;; 使用泛型函数
#lang racket
(require "tag-datum.rkt")
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(provide (all-defined-out))

;; 泛型操作
(define (apply-generic op . args)
  (let ((type-tags (map type-tag args)))
    (let ((proc (get op type-tags)))
      (if (not (null? proc))
          (apply proc (map contents args))
          (if (= (length args) 2)
              (let ((type1 (car type-tags))
                    (type2 (cadr type-tags))
                    (a1 (car args))
                    (a2 (cadr args)))
                ;; 如果两个输入数据类型相同，报错
                (if (equal? type1 type2)
                    (error "No method for these types")
                    (let ((t1->t2 (get-coercion type1 type2))
                          (t2->t1 (get-coercion type2 type1)))
                      (cond ((not (null? t1->t2))
                             (apply-generic op (t1->t2 a1) a2))
                            ((not (null? t2->t1))
                             (apply-generic op a1 (t2->t1 a2)))
                            (else
                             (error "No method for these types"
                                    (list op type-tags)))))))
              (error "No method for these types"
                     (list op type-tags)))))))

;; 获取转换函数
(define (get-coercion type1 type2)
  (get 'coercion (list type1 type2)))
 
    
  练习2.82 
  这种实现方式，如果存在输入类型不同的通用函数，比如(exp scheme-number complex)，是不能找到这个通用函数的，只能找到所有输入类型都是一样的通用函数 
  ;; Exercise 2.81
;; 使用泛型函数
#lang racket
(require "tag-datum.rkt")
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(provide (all-defined-out))

;; 多输入泛型操作
(define (apply-generic op . args)
  ;; 尝试转换arg为type类型
  (define (change-type type)
    (lambda(arg)
      (let ((change-proc (get-coercion (type-tag arg) type)))
        (if (null? change-proc)
             arg
             (change-proc arg)))))
  ;; origin-types表示最初输入参数的类型list
  (define (iter origin-types changed-args)
    ;; 查找对应输入类型的函数
    (let ((type-tags (map type-tag changed-args)))
      (let ((proc (get op type-tags)))
        (if (not (null? proc))
            ;; 如果找到对应输入类型的函数
            (apply proc (map contents changed-args))
            ;; 如果没有找到，转换为origin-types中的首元素类型
            (if (null? origin-types)
                ;; 已经尝试了所有类型，仍未找到，报错
                (error "No method for these types")
                ;; 转换参数类型，递归调用
                (iter (cdr origin-types) (map (change-type (car origin-types)) args)))))))
  ;; 调用
  (iter (map type-tag args) args))
          
;; 获取转换函数
(define (get-coercion type1 type2)
  (get 'coercion (list type1 type2))) 
    
  练习2.83 
  先写好integer和real的包 
  ;; 整数包
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "install-rational-package.rkt")
(provide (all-defined-out))

;; 安装整数包
(define (install-integer-package)
  ;; internal procedures
  (define (make-integer x)
    x)
  ;; 升级为有理数
  (define (raise-integer x)
    ((get 'make 'rational) x 1))
  ;; interface to rest of the system
  (define (tag x) (attach-tag 'integer x))
  (put 'make 'integer
       (lambda (x) (tag (make-integer x))))
  (put 'raise '(integer)
       raise-integer)
  ;; 判断是否相等
  (put 'equ? '(integer integer)
       (lambda (x y) (= x y)))
  'done)

  ;; 构造函数
(define (make-integer x)
  ((get 'make 'integer) x))
 
  ;; 实数包
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "install-complex-package.rkt")
(provide (all-defined-out))

;; 安装实数包
(define (install-real-package)
  ;; internal procedures
  (define (make-real x)
    x)
  ;; 升级为复数
  (define (raise-real x)
    ((get 'make-from-real-imag 'complex) x 0))
  ;; interface to rest of the system
  (define (tag x) (attach-tag 'real x))
  (put 'make 'real
       (lambda (x) (tag (make-real x))))
  (put 'raise '(real)
       raise-real)
  ;; 判断是否相等
  (put 'equ? '(real real)
       (lambda (x y) (= x y)))
  'done)

  ;; 构造函数
(define (make-real x)
  ((get 'make 'real) x)) 
  rational包添加raise函数 
  ;; 升级为实数
(define (raise-rational r)
  ((get 'make 'real) (/ (numer r) (denom r))))
(put 'raise '(rational) raise-rational) 
    
  练习2.84 
  类型关系用了hash表来模拟 
  ;; 模拟类型塔
(define levels (hash 'integer 3 'rational 2 'real 1 'complex 0))

;; 带raise的多输入泛型操作
(define (apply-generic-with-raise op . args)
  ;; raise到指定类型
  (define (raise-to type)
    (lambda(arg)
      (define (iter cur)
        (if (equal? type (type-tag cur))
            cur
            (let ((proc (get 'raise (list (type-tag cur)))))
              (if (null? proc)
                  (error "Cannot raise")
                  (iter (proc (contents cur)))))))
      (iter arg)))
  ;; 找到输入参数中最高级类型
  (define (highest-type args)
    (define (iter remains higher)
      (if (null? remains)
          (type-tag higher)
          (let ((arg (car remains)))
            (if (> (hash-ref levels (type-tag arg)) (hash-ref levels (type-tag higher)))
                (iter (cdr remains) arg)
                (iter (cdr remains) arg)))))
    (iter (cdr args) (car args)))
;; 找到参数中最高级类型，把所有参数转换为该类型，寻找对应通用函数
  (let ((changed-proc (raise-to (highest-type args))))
    (let ((changed-args (map changed-proc args)))
      (let ((proc (get op (map type-tag changed-args))))
        (if (null? proc)
            (error "No method for these types")
            (apply proc (map contents changed-args))))))) 
    
  练习2.85 
  要求写出一个drop程序，把某个类型尽可能地降级成低级的类型，直到不能转换为止（例如复数3+4i降级成实数，会损失虚部） 
  关键在于如何判断是否可以转换成低级类型，即是否降级会造成误差，题目给出的方法是，写一个project函数，把一个类型降级，再调用raise提升回原类型，判断得到的数据是否和原来相等，如果相等，就证明降级不会造成误差 
  首先，在每个类里加上project这个函数 
  ;; 降级为整数
(define (project-rational r)
  ((get 'make 'integer) (round (/ (numer r) (denom r)))))
(put 'project '(rational) project-rational) 
  ;; 降级为有理数
(define (project-real x)
  ((get 'make 'rational) (* x 100000000) 100000000))
(put 'project '(real) project-real)   
  ;; 降级为实数
(define (project-complex c)
  ((get 'make 'real) (real-part c)))
(put 'project '(complex) project-complex) 
  最后写出drop函数 
  ;; Exercise 2.85
;; 数据类型降级
#lang racket
(require "apply-generic.rkt")
(require "tag-datum.rkt")
(provide (all-defined-out))

;; 数据降级
(define (apply-drop arg)
  (if (equal? (type-tag arg) 'integer)
      arg
      ;; 尝试降级
      (let ((projected-arg (apply-generic 'project arg)))
        ;; 判断降级后数据，raise后是否等于原数据
        (if (apply-generic 'equ? arg (apply-generic 'raise projected-arg))
            (apply-drop projected-arg)
            arg))))
 
    
  练习2.86 
  为了不和以前的代码混淆，创建新类new-complex、new-rectangular-complex和new-polar-complex 
  要注意构造函数不能再用cons，而要改用list，因为(cons (cons 'integer 3) (cons 'integer 3))的结果是((cons 'integer 3) 'integer 3) 
  很简单，把每个+、-、*、/、sqrt、square之类的操作全部用apply-generic替换，代码如下 
  ;; Exercise 2.86
;; 新复数包，实部和虚部可以用任意数字类型表示
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "install-new-rectangular-package.rkt")
(require "install-new-polar-package.rkt")
(require "apply-generic.rkt")
(provide (all-defined-out))

;; 安装复数子包
(install-new-rectangular-package)
(install-new-polar-package)

;; select
(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))

;; 安装新复数包
(define (install-new-complex-package)
  ;; imported procedures from rectangular and polar packages
  (define (make-from-real-imag x y)
    ((get 'make-from-real-imag 'rectangular) x y))
  (define (make-from-mag-ang r a)
    ((get 'make-from-mag-ang 'polar) r a))
  ;; internal procedures
  (define (add-complex z1 z2)
    (make-from-real-imag
     (apply-generic 'add (real-part z1) (real-part z2))
     (apply-generic 'add (imag-part z1) (imag-part z2))))
  (define (sub-complex z1 z2)
    (make-from-real-imag (apply-generic 'sub (real-part z1) (real-part z2))
                         (apply-generic 'sub (imag-part z1) (imag-part z2))))
  (define (mul-complex z1 z2)
    (make-from-mag-ang (apply-generic 'mul (magnitude z1) (magnitude z2))
                       (apply-generic 'add (angle z1) (angle z2))))
  (define (div-complex z1 z2)
    (make-from-mag-ang (apply-generic 'div (magnitude z1) (magnitude z2))
                       (apply-generic 'sub (angle z1) (angle z2))))
  ;; 判断复数是否相等
  (define (equ? z1 z2)
    (and (apply-generic 'equ? (real-part z1) (real-part z2)) (apply-generic 'equ? (imag-part z1) (imag-part z2))))
  ;; 判断复数是否为零
  (define (complex-zero? c)
    (and (apply-generic 'zero? (real-part c)) (apply-generic 'zero? (imag-part c))))
  ;; 降级为实数
  (define (project-complex c)
    ((get 'make 'real) (real-part c)))
  ;; interface to rest of the system
  (define (tag z) (attach-tag 'complex z))
  (put 'add '(complex complex)
       (lambda (z1 z2) (tag (add-complex z1 z2))))
  (put 'sub '(complex complex)
       (lambda (z1 z2) (tag (sub-complex z1 z2))))
  (put 'mul '(complex complex)
       (lambda (z1 z2) (tag (mul-complex z1 z2))))
  (put 'div '(complex complex)
       (lambda (z1 z2) (tag (div-complex z1 z2))))
  (put 'make-from-real-imag 'complex
       (lambda (x y) (tag (make-from-real-imag x y))))
  (put 'make-from-mag-ang 'complex
       (lambda (r a) (tag (make-from-mag-ang r a))))
  (put 'real-part '(complex) real-part)
  (put 'imag-part '(complex) imag-part)
  (put 'magnitude '(complex) magnitude)
  (put 'angle '(complex) angle)
  (put 'equ? '(complex complex) equ?)
  (put 'zero? '(complex) complex-zero?)
  (put 'project '(complex) project-complex)
  'done)

;; 构造函数
(define (make-complex-from-real-imag x y)
  ((get 'make-from-real-imag 'complex) x y))
(define (make-complex-from-mag-ang r a)
  ((get 'make-from-mag-ang 'complex) r a))
 
    
  ;; Exercise 2.86
;; 新直角坐标复数包，支持任意数字类型
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "apply-generic.rkt")
(provide (all-defined-out))

;; 安装新直角坐标复数包
(define (install-new-rectangular-package)
  ;; internal procedures
  (define (real-part z) (car z))
  (define (imag-part z) (cadr z))
  (define (make-from-real-imag x y) (list x y))
  (define (magnitude z)
    (apply-generic 'square
                   (apply-generic 'add
                                  (apply-generic 'square (real-part z))
                                  (apply-generic 'square (imag-part z)))))
  (define (angle z)
    (apply-generic 'atan (imag-part z) (real-part z)))
  (define (make-from-mag-ang r a) 
    (cons
     (apply-generic 'mul r (apply-generic 'cos a))
     (apply-generic 'mul r (apply-generic 'sin a))))
  ;; interface to the rest of the system
  (define (tag x) (attach-tag 'rectangular x))
  (put 'real-part '(rectangular) real-part)
  (put 'imag-part '(rectangular) imag-part)
  (put 'magnitude '(rectangular) magnitude)
  (put 'angle '(rectangular) angle)
  (put 'make-from-real-imag 'rectangular 
       (lambda (x y) (tag (make-from-real-imag x y))))
  (put 'make-from-mag-ang 'rectangular 
       (lambda (r a) (tag (make-from-mag-ang r a))))
  'done)

;; 构造函数
(define (make-from-real-imag x y)
  ((get 'make-from-real-imag 'rectangular) x y))
 
    
  ;; 新极坐标复数包，支持任意数字类型
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "apply-generic.rkt")
(provide (all-defined-out))

;; 安装新极坐标复数包
(define (install-new-polar-package)
  ;; internal procedures
  (define (magnitude z) (car z))
  (define (angle z) (cadr z))
  (define (make-from-mag-ang r a) (list r a))
  (define (real-part z)
    (apply-generic 'mul (magnitude z) (cos (angle z))))
  (define (imag-part z)
    (apply-generic 'mul (magnitude z) (sin (angle z))))
  (define (make-from-real-imag x y) 
    (cons (apply-generic 'sqrt (apply-generic 'add (* x x) (* y y)))
          (apply-generic 'atan y x)))
  ;; interface to the rest of the system
  (define (tag x) (attach-tag 'polar x))
  (put 'real-part '(polar) real-part)
  (put 'imag-part '(polar) imag-part)
  (put 'magnitude '(polar) magnitude)
  (put 'angle '(polar) angle)
  (put 'make-from-real-imag 'polar
       (lambda (x y) (tag (make-from-real-imag x y))))
  (put 'make-from-mag-ang 'polar 
       (lambda (r a) (tag (make-from-mag-ang r a))))
  'done)

;; 构造函数
(define (make-from-mag-ang r a)
  ((get 'make-from-mag-ang 'polar) r a)) 
  现在给scheme-number类添加add、sub等函数，以便complex调用 
  ;; 数字包
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "install-rational-package.rkt")
(provide (all-defined-out))

;; 数字包
(define (install-scheme-number-package)
  (define (tag x)
    (attach-tag 'scheme-number x))
  ;; 判断数字是否为0
  (define (number-zero? n)
    (= n 0))
  (put 'add '(scheme-number scheme-number)
       (lambda (x y) (tag (+ x y))))
  (put 'sub '(scheme-number scheme-number)
       (lambda (x y) (tag (- x y))))
  (put 'mul '(scheme-number scheme-number)
       (lambda (x y) (tag (* x y))))
  (put 'div '(scheme-number scheme-number)
       (lambda (x y) (tag (/ x y))))
  (put 'square '(scheme-number)
       (lambda (x) (* x x)))
  (put 'sqrt '(scheme-number)
       (lambda (x) (sqrt x)))
  (put 'sin '(scheme-number)
       (lambda (x) (sin x)))
  (put 'cos '(scheme-number)
       (lambda (x) (cos x)))
  (put 'atan '(scheme-number)
       (lambda (x) (atan x)))
  (put 'make 'scheme-number
       (lambda (x) (tag x)))
  ;; 判断数字是否相等
  (put 'equ? '(scheme-number scheme-number) =)
  (put 'zero? '(scheme-number) number-zero?)
  ;; 指数计算
  (put 'exp '(scheme-number scheme-number)
       (lambda (x y) (tag (expt x y))))
  'done)

;; 构造函数
(define (make-scheme-number x)
  ((get 'make 'scheme-number) x))
 
  写一个代码测试一下 
  (define c1 (make-complex-from-real-imag (make-scheme-number 3) (make-scheme-number 4)))
(define c2 (make-complex-from-real-imag (make-scheme-number 7) (make-scheme-number 5)))
(apply-generic 'add c1 c2)
 
  输出 
   
    
  练习2.87 
  ;; 判断该项是否为0
(define (=zero? n1) (apply-generic 'zero? n1)) 
    
  练习2.88 
  减法可以转换为加法来做，只要给每个代数包加上一个求负数的函数就可以 
  在多项式包里增加减法 
  ;; 多项式减法
(define (sub-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
    (make-poly (variable p1)
               (sub-terms (term-list p1)
                          (term-list p2)))
    (error "Polys not in same var -- SUB-POLY"
           (list p1 p2))))
(define (sub-terms L1 L2)
  ;; 将多项式的一项系数取负
  (define (negation-term term)
    (list (order term) (apply-generic 'negation (coeff term))))
  (add-terms L1 (map negation-term L2)))

(put 'sub '(polynomial polynomial) 
     (lambda (p1 p2) (tag (sub-poly p1 p2))
 
  举个例子，在scheme-number包里增加求负数的方法 
  ;; 求负数
(put 'negation '(scheme-number)
     (lambda (x) (tag (- x)))) 
    
  练习2.89 
  用稠密表示法，系数的结构很简单，一个list就可以搞定，从0阶开始排列，然后重写加法、减法和乘法，整个类的代码如下 
  ;; 多项式包，稠密表示法
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "apply-generic.rkt")
(require "install-polynomial-parse-package.rkt")
(provide (all-defined-out))

(define (install-polynomial-dense-package)
  ;; internal procedures
  ;; representation of poly
  (define (make-poly variable term-list)
    (cons variable term-list))
  (define (variable p) (car p))
  (define (term-list p) (cdr p))
  ;; 返回稀疏表示法的稀疏list
  (define (parse-terms p)
    (define (iter cur remains res)
      (if (null? remains)
          res
          (iter (+ cur 1) (cdr remains) (cons (list cur (car remains)) res))))
    (iter 0 p null))
  ;; 稠密转稀疏
  (define (dense-to-parse p)
    (let ((content (contents p)))
      (make-polynomial-parse (variable content) (parse-terms (term-list content)))))
  ;; 判断是否是同一变量
  (define (same-variable? x y)
    (equal? x y))
  ;; 多项式加法
  (define (add-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (make-poly (variable p1)
                 (add-terms (term-list p1)
                            (term-list p2)))
      (error "Polys not in same var -- ADD-POLY"
             (list p1 p2))))
  ;; 多项式乘法
  (define (mul-poly p1 p2)
    (if (same-variable? (variable p1) (variable p2))
        (make-poly (variable p1)
                   (mul-terms (term-list p1)
                              (term-list p2)))
        (error "Polys not in same var -- MUL-POLY"
               (list p1 p2))))
  ;; 多项式减法
  (define (sub-poly p1 p2)
    (if (same-variable? (variable p1) (variable p2))
        (make-poly (variable p1)
                   (sub-terms (term-list p1)
                              (term-list p2)))
        (error "Polys not in same var -- ADD-POLY"
               (list p1 p2))))
  ;; term-list
  (define (sub-terms L1 L2)
    ;; 将多项式的一项系数取负
    (define (negation-term term)
      (apply-generic 'sub 0 term))
    (add-terms L1 (map negation-term L2)))
  (define (add-terms L1 L2)
    (cond ((empty-termlist? L1) L2)
          ((empty-termlist? L2) L1)
          (else
           (cons (apply-generic 'add (first-term L1) (first-term L2))
                 (add-terms (rest-terms L1) (rest-terms L2))))))
  (define (mul-terms L1 L2)
    (if (empty-termlist? L1)
        (the-empty-termlist)
        (add-terms (mul-term-by-all-terms (first-term L1) L2)
                   (mul-terms (rest-terms L1) (cons 0 L2)))))
  (define (mul-term-by-all-terms t1 L)
    (if (empty-termlist? L)
        (the-empty-termlist)
        (map (lambda (x) (apply-generic 'mul x t1)) L)))
  (define (the-empty-termlist) '())
  (define (first-term term-list) (car term-list))
  (define (rest-terms term-list) (cdr term-list))
  (define (empty-termlist? term-list) (null? term-list))
  ;; interface to rest of the system
  (define (tag p) (attach-tag 'polynomial-dense p))
  (put 'add '(polynomial-dense polynomial-dense) 
       (lambda (p1 p2) (tag (add-poly p1 p2))))
  (put 'mul '(polynomial-dense polynomial-dense) 
       (lambda (p1 p2) (tag (mul-poly p1 p2))))
  (put 'sub '(polynomial-dense polynomial-dense) 
       (lambda (p1 p2) (tag (sub-poly p1 p2))))
  (put 'make 'polynomial-dense
       (lambda (var terms) (tag (make-poly var terms))))
  (put 'coercion '(polynomial-dense polynomial-parse) dense-to-parse)
  'done)

;; 构造函数
(define (make-polynomial-dense variable term-list)
  ((get 'make 'polynomial-dense) variable term-list))

(install-polynomial-dense-package) 
    
  练习2.90 
  把原来的多项式包改一下标签和包名，变为稀疏指数包，再和练习2.89里的稠密多项式包一起作为多项式包的两个子包 
  ;; 多项式包，稀疏表示法
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "apply-generic.rkt")
(provide (all-defined-out))

(define (install-polynomial-parse-package)
  ;; internal procedures
  ;; representation of poly
  (define (make-poly variable term-list)
    (cons variable term-list))
  (define (variable p) (car p))
  (define (term-list p) (cdr p))
  ;; 判断是否是同一变量
  (define (same-variable? x y)
    (equal? x y))
  ;; 多项式加法
  (define (add-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (make-poly (variable p1)
                 (add-terms (term-list p1)
                            (term-list p2)))
      (error "Polys not in same var -- ADD-POLY"
             (list p1 p2))))
  ;; 多项式乘法
  (define (mul-poly p1 p2)
    (if (same-variable? (variable p1) (variable p2))
        (make-poly (variable p1)
                   (mul-terms (term-list p1)
                              (term-list p2)))
        (error "Polys not in same var -- MUL-POLY"
               (list p1 p2))))
  ;; 多项式减法
  (define (sub-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (make-poly (variable p1)
                 (sub-terms (term-list p1)
                            (term-list p2)))
      (error "Polys not in same var -- SUB-POLY"
             (list p1 p2))))
  ;; term-list
  (define (sub-terms L1 L2)
    ;; 将多项式的一项系数取负
    (define (negation-term term)
      (list (order term) (apply-generic 'negation (coeff term))))
    (add-terms L1 (map negation-term L2)))
  (define (add-terms L1 L2)
    (cond ((empty-termlist? L1) L2)
          ((empty-termlist? L2) L1)
          (else
           (let ((t1 (first-term L1)) (t2 (first-term L2)))
             (cond ((> (order t1) (order t2))
                    (adjoin-term t1 (add-terms (rest-terms L1) L2)))
                   ((< (order t1) (order t2))
                    (adjoin-term t2 (add-terms L1 (rest-terms L2))))
                   (else
                    (adjoin-term
                     (make-term (order t1)
                                (add (coeff t1) (coeff t2)))
                     (add-terms (rest-terms L1)
                                (rest-terms L2)))))))))
  (define (mul-terms L1 L2)
    (if (empty-termlist? L1)
        (the-empty-termlist)
        (add-terms (mul-term-by-all-terms (first-term L1) L2)
                   (mul-terms (rest-terms L1) L2))))
  (define (mul-term-by-all-terms t1 L)
    (if (empty-termlist? L)
        (the-empty-termlist)
        (let ((t2 (first-term L)))
          (adjoin-term
           (make-term (+ (order t1) (order t2))
                      (mul (coeff t1) (coeff t2)))
           (mul-term-by-all-terms t1 (rest-terms L))))))
  (define (adjoin-term term term-list)
    (if (=zero? (coeff term))
        term-list
        (cons term term-list)))
  (define (the-empty-termlist) '())
  (define (first-term term-list) (car term-list))
  (define (rest-terms term-list) (cdr term-list))
  (define (empty-termlist? term-list) (null? term-list))
  (define (make-term order coeff) (list order coeff))
  (define (order term) (car term))
  (define (coeff term) (cadr term))
  ;; interface to rest of the system
  (define (tag p) (attach-tag 'polynomial-parse p))
  (put 'add '(polynomial-parse polynomial-parse) 
       (lambda (p1 p2) (tag (add-poly p1 p2))))
  (put 'mul '(polynomial-parse polynomial-parse) 
       (lambda (p1 p2) (tag (mul-poly p1 p2))))
  (put 'sub '(polynomial-parse polynomial-parse) 
       (lambda (p1 p2) (tag (sub-poly p1 p2))))
  (put 'make 'polynomial-parse
       (lambda (var terms) (tag (make-poly var terms))))
  'done)

;; 构造函数
(define (make-polynomial-parse variable term-list)
  ((get 'make 'polynomial-parse) variable term-list))

(define (add n1 n2) (apply-generic 'add n1 n2))
(define (mul n1 n2) (apply-generic 'mul n1 n2))
;; 判断该项是否为0
(define (=zero? n1) (apply-generic 'zero? n1))

(install-polynomial-parse-package) 
  多项式包除了提供一些对外的接口，还要处理两个不同表示法的多项式数据进行计算的情况，一个思路是，把两个参数转换为同一个表示法，从稠密转稀疏更加简单一些，所以我用了这种，在稠密表示法中增加一个类型转换方法 
  ;; 返回稀疏表示法的稀疏list
(define (parse-terms p)
  (define (iter cur remains res)
    (if (null? remains)
        res
        (iter (+ cur 1) (cdr remains) (cons (list cur (car remains)) res))))
  (iter 0 p null))
;; 稠密转稀疏
(define (dense-to-parse p)
  (make-polynomial-parse (variable p) (parse-terms p)))

(put 'coercion '(polynomial-dense polynomial-parse) dense-to-parse) 
  多项式包如下 
  ;; 多项式包
#lang racket
(require (file "../2.4.3 Data-Directed Programming and Additivity/funcs-table.rkt"))
(require "tag-datum.rkt")
(require "apply-generic.rkt")
(require "install-polynomial-parse-package.rkt")
(require "install-polynomial-dense-package.rkt")
(provide (all-defined-out))

(define (install-polynomial-package)
  ;; internal procedures
  ;; 多项式加法
  (define (add-poly p1 p2) (apply-generic 'add p1 p2))
  ;; 多项式乘法
  (define (mul-poly p1 p2) (apply-generic 'mul p1 p2))
  ;; 多项式减法
  (define (sub-poly p1 p2) (apply-generic 'sub p1 p2))
  ;; interface to rest of the system
  (put 'add '(polynomial polynomial) 
       (lambda (p1 p2) (tag (add-poly p1 p2))))
  (put 'mul '(polynomial polynomial) 
       (lambda (p1 p2) (tag (mul-poly p1 p2))))
  (put 'sub '(polynomial polynomial) 
       (lambda (p1 p2) (tag (sub-poly p1 p2))))
  'done)

(define (tag p) (attach-tag 'polynomial p))
;; 构造函数
(define (make-polynomial-from-dense variable term-list)
  (tag ((get 'make 'polynomial-dense) variable term-list)))
(define (make-polynomial-from-parse variable term-list)
  (tag ((get 'make 'polynomial-parse) variable term-list)))

(install-polynomial-package) 
  测试一下 
  (require "install-polynomial-package.rkt")
(require "install-scheme-number-package.rkt")
(require "apply-generic.rkt")

(define n1 (make-scheme-number 1))
(define n2 (make-scheme-number 2))
(define n3 (make-scheme-number 3))
(define n4 (make-scheme-number 4))
  
(define p1 (make-polynomial-from-dense 'x (list n1 n3 n4)))
(define p2 (make-polynomial-from-dense 'x (list n1 n3 n2)))
(define p3 (make-polynomial-from-parse 'x (list
                                           (list 100 n3)
                                           (list 3 n4)
                                           (list 1 n1))))
(define p4 (make-polynomial-from-parse 'x (list
                                           (list 5 n3)
                                           (list 3 n1)
                                           (list 1 n1))))

(display "测试稠密表示法\n")
(apply-generic 'add p1 p2)
(apply-generic 'sub p1 p2)
(apply-generic 'mul p1 p2)

(display "测试稀疏表示法\n")
(apply-generic 'add p3 p4)
(apply-generic 'sub p3 p4)
(apply-generic 'mul p3 p4)

(display "测试混合类型计算\n")
(define p5 (make-polynomial-from-dense 'x (list n2 n3 n4)))
(define p6 (make-polynomial-from-parse 'x (list
                                           (list 4 n3)
                                           (list 2 n4)
                                           (list 1 n1))))
(apply-generic 'add p5 p6)
(apply-generic 'sub p5 p6)
(apply-generic 'mul p5 p6)
 
   
   
   
    
  练习2.91 
  在稀疏包插入下面的代码，当然还要在稀疏包和多项式包里都加上各种put，略去不写 
  ;; 多项式除法
(define (div-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (let ((res (div-terms (term-list p1) (term-list p2))))
        (list (tag (make-poly (variable p1)
                              (car res)))
              (tag (make-poly (variable p2)
                              (cadr res)))))
      (error "Polys not in same var -- DIV-POLY"
             (list p1 p2))))
;; 除法
(define (div-terms L1 L2)
    (if (empty-termlist? L1)
      (list (the-empty-termlist) (the-empty-termlist))
      (let ((t1 (first-term L1))
            (t2 (first-term L2)))
        (if (> (order t2) (order t1))
            (list (the-empty-termlist) L1)
            (let ((new-c (apply-generic 'div (coeff t1) (coeff t2)))
                  (new-o (- (order t1) (order t2))))
              (let ((rest-of-result
                     (div-terms
                      (sub-terms
                       L1
                       (mul-terms L2 (list (list new-o new-c))))
                      L2)
                     ))
                (list (adjoin-term
                       (list new-o new-c)
                       (car rest-of-result))
                      (cadr rest-of-result))
                )))))) 
    
  练习2.92 
  题目的意思是，给定一个变量的优先级序列，当低优先级变量多项式和高优先级多项式相加时，低优先级变量就当做常量来处理 
  做了很久，怎么写都觉得不优雅，算了直接发 
  这里只用稀疏表示法来做 
  首先，给出个判断变量优先级的模块，可以比较两个变量的优先级高低 
  ;; 判断变量优先级
#lang racket
(provide (all-defined-out))

;; 优先级列表
(define priority (make-hash (list (cons 'x 0) (cons 'y 1) (cons 'z 2))))

;; 判断优先级
(define (higher-priority? x y)
  (let ((n1 (hash-ref priority x))
        (n2 (hash-ref priority y)))
    (> n1 n2))) 
  然后，当某个变量多项式因为优先级低降级为系数，就需要处理多项式和数字相加的情况，因此数字包里需要增加一个转换为多项式的代码 
  ;; 转换为多项式
(put 'to-polynomial '(symbol scheme-number)
     (lambda (var x) (make-polynomial-parse var (list (list 0 x))))) 
  现在来修改稀疏包里的加法函数，需要修改两个地方：其一，之前加法判断两个变量不相同就报错，现在修改为，两个变量不同，判断优先级，将低优先级的变量多项式转化为系数；其二，要支持多项式和数字的相加 
  对于其一，修改add-poly代码很容易解决 
  对于其二， 修改add-poly里的代码肥肠难做到松耦合，因为多项式在调用到add-poly的时候，已经去掉了tag，所以要判断加法的两个参数类型是多项式还是数字，所以我给数字包增加了一个标记，在数字包里加入这样一个函数，然后就可以通过调用(apply-generic 'isNumber? n)判断n是不是数字了，所有实现这个标记的数字包都可以在多项式包里作为系数使用 
  ;; 数字标记
(put 'isNumber? 'scheme-number true) 
  系数有可能是多项式，那么zero?的代码也要修改，兼容多项式的判断 
  ;; 判断该项是否为0
(define (=zero? n1)
  (if (isNumber? n1)
      (apply-generic 'zero? n1)
      (null? (term-list n1)))) 
  最后add的代码是这样的 
  add-poly，判断两个多项式的变量是否相同，如果相同直接调用add-terms，变量不同，把低优先级的多项式变为系数，在调用add-poly 
  add-terms，没有变化，改变的是调用的add函数 
  add，原来add是直接apply-generic，现在改一下，让他支持多项式和数字的相加，方法是把数字转换为多项式再调用add-poly计算 
  ;; 多项式加法
(define (add-poly p1 p2)
  (let ((var1 (variable p1))
        (var2 (variable p2)))
    (if (same-variable? var1 var2)
        (make-poly var1
                   (add-terms (term-list p1)
                              (term-list p2)))
        ;; 如果变量不同，判断优先级
        (if (higher-priority? var1 var2)
            (add-poly p1 (make-poly var1 (list (list 0 p2))))
            (add-poly (make-poly var2 (list (list 0 p1))) p2))))) 
(define (add-terms L1 L2)
   (cond ((empty-termlist? L1) L2)
         ((empty-termlist? L2) L1)
         (else
           (let ((t1 (first-term L1)) (t2 (first-term L2)))
             (cond ((> (order t1) (order t2))
                    (adjoin-term t1 (add-terms (rest-terms L1) L2)))
                   ((< (order t1) (order t2))
                    (adjoin-term t2 (add-terms L1 (rest-terms L2))))
                   (else
                    (adjoin-term
                     (make-term (order t1)
                                (add (coeff t1) (coeff t2)))
                     (add-terms (rest-terms L1)
                                (rest-terms L2)))))))))
;; 加法计算
;; 如果两项均为数字，直接调用该数字类型的加法
;; 如果是多项式和数字，则数字升级为多项式，进行加法计算
;; 如果是两个多项式，直接调用add-poly
(define (add n1 n2)
  (cond ((and (isNumber? n1) (isNumber? n2)) (apply-generic 'add n1 n2))
        ((isNumber? n1) (tag (add-poly (contents (apply-generic 'to-polynomial (variable n2) n1)) n2)))
        ((isNumber? n2) (tag (add-poly n1 (contents (apply-generic 'to-polynomial (variable n1) n2)))))
        (else (add-poly n1 n2))))
;; 判断是否是数字
(define (isNumber? x)
  (let ((flag (get 'isNumber? (type-tag x))))
    (not (null? flag)))) 
  乘法照着加法的方法类似地做，不再多说 
  ;; 多项式乘法
(define (mul-poly p1 p2)
  (let ((var1 (variable p1))
        (var2 (variable p2)))
    (if (same-variable? var1 var2)
        (make-poly (variable p1)
                   (mul-terms (term-list p1)
                              (term-list p2)))
        (if (higher-priority? var1 var2)
            (mul-poly p1 (make-poly var1 (list (list 0 p2))))
            (mul-poly (make-poly var2 (list (list 0 p1))) p2)))))
(define (mul-terms L1 L2)
    (if (empty-termlist? L1)
        (the-empty-termlist)
        (add-terms (mul-term-by-all-terms (first-term L1) L2)
                   (mul-terms (rest-terms L1) L2))))
  (define (mul-term-by-all-terms t1 L)
    (if (empty-termlist? L)
        (the-empty-termlist)
        (let ((t2 (first-term L)))
          (adjoin-term
           (make-term (+ (order t1) (order t2))
                      (mul (coeff t1) (coeff t2)))
           (mul-term-by-all-terms t1 (rest-terms L))))))
;; 乘法计算
;; 如果两个都是数字，调用apply-generic
;; 如果是多项式和数字，把数字变为多项式计算
;; 如果是两个多项式，直接调用mul-poly
(define (mul n1 n2)
  (cond ((and (isNumber? n1) (isNumber? n2)) (apply-generic 'mul n1 n2))
        ((isNumber? n1) (tag (mul-poly (contents (apply-generic 'to-polynomial (variable n2) n1)) n2)))
        ((isNumber? n2) (tag (mul-poly n1 (contents (apply-generic 'to-polynomial (variable n1) n2)))))
        (else (mul-poly n1 n2)))) 
  测试一下 
  (display "测试多变量\n")
(define p9 (make-polynomial-from-parse 'x (list
                                           (list 5 n1)
                                           (list 0 n-1))))
(define p10 (make-polynomial-from-parse 'y (list
                                            (list 2 n1)
                                            (list 0 n-1))))
(apply-generic 'add p9 p10)
(apply-generic 'mul p9 p10) 
   
    
  练习2.93 
  要把rational包里的*、+等替换为apply-generic 
  (define (numer x) (car x))
(define (denom x) (cadr x))
(define (make-rat n d)
  (list n d))
;; 计算
(define (add x y) (apply-generic 'add x y))
(define (mul x y) (apply-generic 'mul x y))
(define (add-rat x y)
  (make-rat (add (mul (numer x) (denom y))
                 (mul (numer y) (denom x)))
            (mul (denom x) (denom y)))) 
  测试 
  (define n1 (make-scheme-number 1))
(define p1 (make-polynomial-parse 'x (list
                                      (list 2 n1)
                                      (list 0 n1))))
(define p2 (make-polynomial-parse 'x (list
                                      (list 3 n1)
                                      (list 0 n1))))
(define rf (make-rational p2 p1))
(apply-generic 'add rf rf)
 
  输出 
   
    
  练习2.94 
  现在给稀疏包增加一个化简的代码 
  ;; 求公因子
(define (gcd-poly p1 p2)
(if (same-variable? (variable p1) (variable p2))
    (make-poly (variable p1)
               (gcd-terms (term-list p1)
                          (term-list p2)))
    (error "Polys not in same var -- DIV-POLY"
           (list p1 p2))))  
(define (gcd-terms a b)
  ;; 求余
  (define (remainder-terms a b)
    (cadr (div-terms a b)))
  (if (empty-termlist? b)
      a
      (gcd-terms b (remainder-terms a b))))

(put 'greatest-common-divisor
     '(polynomial-parse polynomial-parse)
     (lambda (p1 p2) (tag (gcd-poly p1 p2)))) 
  测试 
  (define p3 (make-polynomial-parse 'x (list
                                      (list 4 (make-scheme-number 1))
                                      (list 3 (make-scheme-number -1))
                                      (list 2 (make-scheme-number -2))
                                      (list 1 (make-scheme-number 2)))))
(define p4 (make-polynomial-parse 'x (list
                                      (list 3 (make-scheme-number 1))
                                      (list 1 (make-scheme-number -1)))))
(apply-generic 'greatest-common-divisor p3 p4)  
   
  代码给出的答案是 
    
  练习2.95 
  撰写测试代码 
  (define p5 (make-polynomial-parse 'x (list
                                      (list 2 (make-scheme-number 1))
                                      (list 1 (make-scheme-number -2))
                                      (list 0 (make-scheme-number 1)))))
(define p6 (make-polynomial-parse 'x (list
                                      (list 2 (make-scheme-number 11))
                                      (list 0 (make-scheme-number 7)))))
(define p7 (make-polynomial-parse 'x (list
                                      (list 1 (make-scheme-number 13))
                                      (list 0 (make-scheme-number 5)))))
(define p8 (apply-generic 'mul p5 p6))
(define p9 (apply-generic 'mul p5 p7))
(apply-generic 'greatest-common-divisor p8 p9)  
  结果肥肠诡异，但是我们把那三个分数都乘以169/1458，就可以得到1，-2，1 
   
  在gcd-terms代码中加入display查看每次迭代做除法的两个数，太长只贴出一部分 
   
   
    
  练习2.96 
  a. 
  为了防止简化后的系数出现分数，在计算公因子的时候，每次除法都给被除数乘上一个整数因子，以保证结果中不会有分数出现 
  举例来说，现在有多项式P和Q，O1和O2是他们的最高阶，c是Q的最高阶项系数，在做多项式除法前，将P乘以系数, 之后再做除法就不会有分数系数产生 
  现在给数字包加一个求factor的函数 
  ;; 返回pseudo的因子
(put 'pseudo-factor '(scheme-number scheme-number scheme-number)
     (lambda (c o1 o2)
       (tag (expt c (+ 1 o1 o2))))) 
  修改gcd 
  (define (gcd-terms a b)
    ;; pseudoremainder-terms，保证结果不出现分数
    (define (pseudoremainder-terms a b)
      (let ((t1 (first-term a))
            (t2 (first-term b)))
          (let ((c (coeff t2))
                (o1 (order t1))
                (o2 (order t2)))
            (let ((factor (apply-generic 'pseudo-factor c o1 o2)))
              (cadr (div-terms (map
                                (lambda (x)
                                  (make-term (order x)
                                             (apply-generic 'mul (coeff x) factor)))
                                a)
                               b))))))
    (if (empty-termlist? b)
        a
        (gcd-terms b (pseudoremainder-terms a b)))) 
  再次运行测试代码，得到的结果 
   
  确实没有分数 
  b. 
  因为乘了很多个整数因子，所以得到的系数变得非常大，现在要将这几个系数化简，就是要先求这几个数字的最大公约数，然后都除以最大公约数 
  首先在数字包加一个求最大公约数的接口 
  ;; 求一组数的最大公约数
(put 'gcd 'scheme-number
     (lambda (L)
       (let ((numbers (map contents L)))
         (tag (apply gcd numbers))))) 
  然后在稀疏包里添加化简系数的代码，把原理的gcd-terms改成gcd-terms-iter 
  ;; 化简后的gcd
(define (gcd-terms a b)
  (simplify-terms (gcd-terms-iter a b)))
;; 系数化简
(define (simplify-terms a)
  (if (empty-termlist? a)
      a
      (let ((coeffs (map coeff a)))
        (let ((g ((get 'gcd (type-tag (car coeffs))) coeffs)))
          (map (lambda (t) (make-term (order t) (apply-generic 'div (coeff t) g))) a))))) 
  再次运行结果 
   
    
  练习2.97 
  a. 
  现在我们要化简两个多项式P和Q，书上给出的方法是首先求出GCD，再分别用pseudo的方法，得到P除GCD、Q除GCD的结果，最后化简系数 
  我很费解，如果GCD都已经是化简过的了，为嘛还要这顿操作，直接除就不会有分数出现啊，算了还是按照书上说的来 
  ;; 两个多项式化简
(define (reduce-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (let ((res (reduce-terms (term-list p1) (term-list p2))))
        (list (tag (make-poly (variable p1)
                              (car res)))
              (tag (make-poly (variable p2)
                              (cadr res)))))
      (error "Polys not in same var -- REDUCE-POLY"
             (list p1 p2))))
(define (reduce-terms a b)
  ;; 系数列表中每个系数乘以或除以一个因子
  (define (factor-terms a factor op)
    (map (lambda (t) (make-term (order t) (apply-generic op (coeff t) factor))) a))
  (let ((g (gcd-terms a b)))
    (let ((factor1 (apply-generic 'pseudo-factor (coeff (first-term g)) (order (first-term a)) (order (first-term g))))
          (factor2 (apply-generic 'pseudo-factor (coeff (first-term g)) (order (first-term b)) (order (first-term g)))))
      (list
       (factor-terms (car (div-terms (factor-terms a factor1 'mul) g)) factor1 'div)
       (factor-terms (car (div-terms (factor-terms b factor2 'mul) g)) factor2 'div)))))

(put 'reduce '(polynomial-parse polynomial-parse)
     (lambda (p1 p2) (reduce-poly p1 p2))) 
  现在再运行一下测试代码 
  (define p5 (make-polynomial-parse 'x (list
                                      (list 2 (make-scheme-number 1))
                                      (list 1 (make-scheme-number -2))
                                      (list 0 (make-scheme-number 1)))))
(define p6 (make-polynomial-parse 'x (list
                                      (list 2 (make-scheme-number 11))
                                      (list 0 (make-scheme-number 7)))))
(define p7 (make-polynomial-parse 'x (list
                                      (list 1 (make-scheme-number 13))
                                      (list 0 (make-scheme-number 5)))))
(define p8 (apply-generic 'mul p5 p6))
(define p9 (apply-generic 'mul p5 p7))

(apply-generic 'reduce p8 p9) 
  化简的结果，和练习2.95里的式子是一致的 
   
  b. 
  在数字包加约分代码 
  ;; 两个数约分
(put 'reduce '(scheme-number scheme-number)
     (lambda (n d)
       (let ((g (gcd n d)))
         (list (/ n g) (/ d g))))) 
  有理数包，修改make函数 
  (define (make-rat n d)
  (apply-generic 'reduce n d)) 
  测试 
   
   
    
  (define p11 (make-polynomial-parse 'x (list (list 1 (make-scheme-number 1)) (list 0 (make-scheme-number 1)))))
(define p12 (make-polynomial-parse 'x (list (list 3 (make-scheme-number 1)) (list 0 (make-scheme-number -1)))))
(define p13 (make-polynomial-parse 'x (list (list 1 (make-scheme-number 1)))))
(define p14 (make-polynomial-parse 'x (list (list 2 (make-scheme-number 1)) (list 0 (make-scheme-number -1)))))

(define rf1 (make-rational p11 p12))
(define rf2 (make-rational p13 p14))

(apply-generic 'add rf1 rf2) 
   
  虽然全都变负了，结果还是很正确的

分类	element-of-set?	adjoin-set	union-set	intersection-set
重复列表	$\Theta (n)$	$\Theta (1)$	$\Theta (n)$	$\Theta (n^2)$
不可重复列表	$\Theta (n)$	$\Theta (n)$	$\Theta (n^2)$	$\Theta (n^2)$

《SICP》习题第2章

你可能感兴趣的:(SICP,SICP,SICP习题)