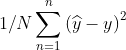线性模型和梯度下降
课程来源:2.线性模型_哔哩哔哩_bilibili
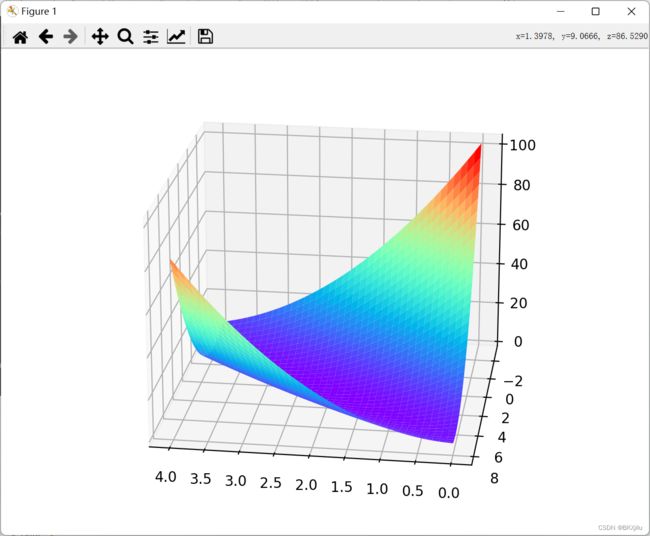
线性模型:y=x*w, 绘制权重w和损失函数的图像,使用穷举法找到最适合的权重w。
代码复现:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#设函数为y=2x+3
x_data = [1.0,2.0,3.0]
y_data = [5.0,7.0,9.0]
def forward(x):
return x * w + b
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
W=np.arange(0.0,4.1,0.1)
B=np.arange(-3.0,8.1,0.1)
#numpy.meshgrid()——生成网格点坐标矩阵
#横坐标矩阵X XX中的每个元素,
# 与纵坐标矩阵Y YY中对应位置元素,共同构成一个点的完整坐标。
# ( X 12 , Y 12 ) = ( 1 , 1 ) (X_{12},Y_{12})
[w,b]=np.meshgrid(W,B)
#w是行向量
print("w",w)
#b是列向量
print("b",b)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
#预测值y,不用再使用for遍历w,b的值。
y_pred_val = forward(x_val)
print(y_pred_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(w, b, l_sum/3,cmap="rainbow")
plt.show()梯度下降算法。
穷举法在数据太多的情况不好用。
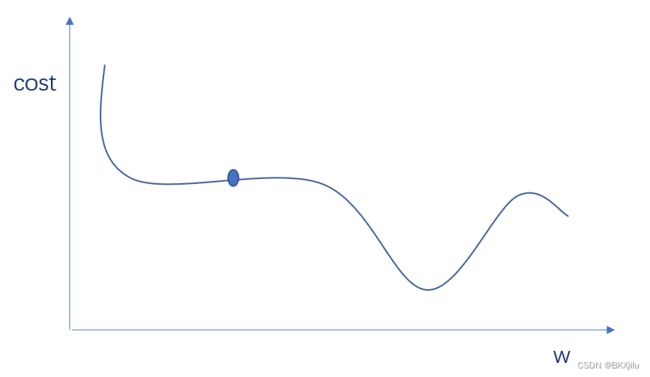
使用梯度下降的算法可以找到局部最优解,在凸函数里面效果很好。
以y=x*w为例:
分别定义求预测值y,求数据集的总损失,求梯度的函数:
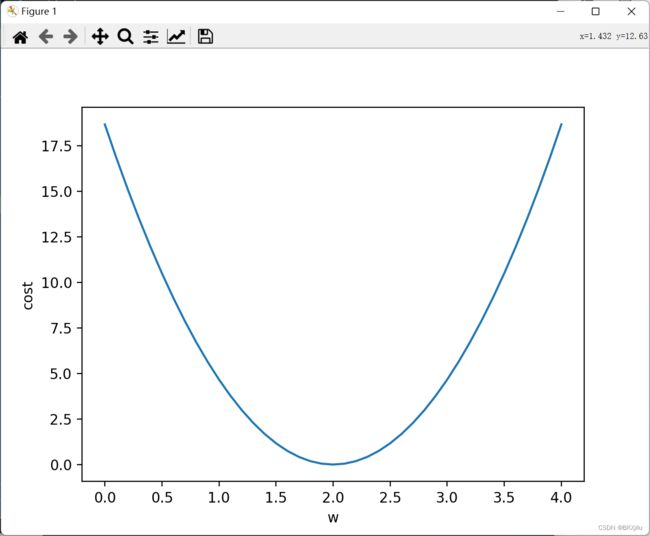
权重和损失函数的图像:
输出epoch(测试轮数),w,cost的值,找到使cost取到最小值的w的值。
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w=1.0
cost2 = []
epoh1 = []
#求预测值y
def forward (x):
return w*x
#求cost
def cost(x1,y1):
cost=0
for x,y in zip(x1,y1):
y_ple = forward(x)
cost += (y_ple-y)**2
return cost / len(x1)
#求梯度
def gra (x1,y1):
#2*x*(x*w+b)
gra=0
for x,y in zip(x1,y1):
gra += 2*x*(x*w-y)
return gra / len(x1)
#变化w的值
for epoh in range(100):
cost1 = cost(x_data,y_data)
gra1 = gra(x_data,y_data)
w-=0.01*gra1
print("epoh:",epoh,"w:",w,"cost",cost1)
cost2.append(cost1)
epoh1.append(epoh)
plt.plot(epoh1,cost2)
plt.ylabel('cost')
plt.xlabel('epoch')
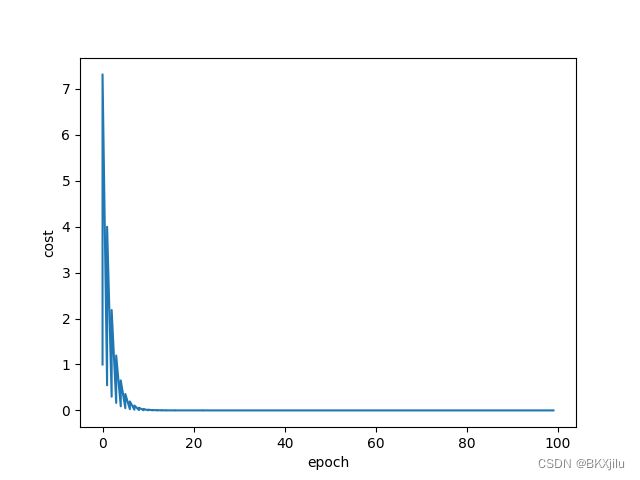
plt.show()
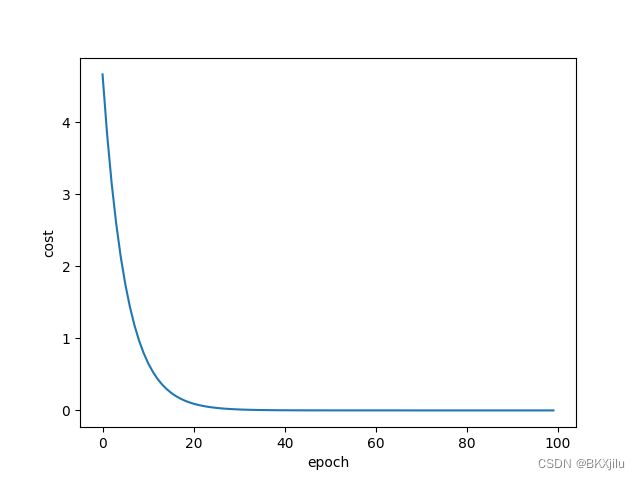
这里显示的是测试轮数与cost的函数。
梯度下降方法有时会进行不了:
为了解决这个情况需要用随机梯度算法:
计算每一个个点的损失loss和梯度,用对应的梯度更新每个点。
loss:![]() ,梯度:
,梯度:![]()
import numpy as np
import matplotlib.pyplot as plt
import random
x_data = [1,2,3]
y_data = [2,4,6]
w=1
loss2 = []
epoh1 = []
#求预测值y
def forward (x):
return w*x
#求loss
def loss(x1,y1):
y_pre=forward (x1)
loss=(y_pre-y1)**2
return loss
#求梯度
def gra (x1,y1):
gra = 2*x1*(x1*w-y1)
return gra
#变化w的值
for epoh in range(100):
for xs,ys in zip(x_data,y_data):
loss1 = loss(xs,ys)
gra1 = gra(xs,ys)
w-=0.01*gra1
print("epoh:",epoh,"w:",w,"loss",loss)
loss2.append(loss1)
epoh1.append(epoh)
plt.plot(epoh1,loss2)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
梯度下降可以并行计算。(因为cost是一样的,xi和xi+1的梯度只和自己有关,并行计算不影响结果)。
随机梯度下降不可以,但是能找到更好的点。
在实际中采取折中的方法:
若干个一组求相应的梯度,更新w。称为小批量的梯度下降 mini-Batch。