pytorch深度学习（3）线性模型

目录

一、线型模型

1. 具体问题：

 机器学习中容易出现的问题：过拟合

2. 建立一个线型模型

 3.损失函数（Loss function）

4.代价函数Cost function

5.运用代码来训练线性模型

---

一、线型模型

1. 具体问题：

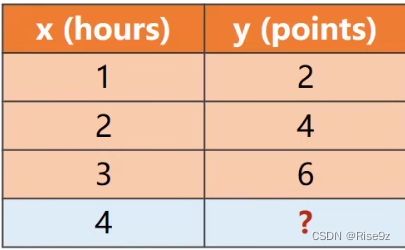
一名学生在学习 x 小时后将会得到 y 得分（如下图），问学习四个小时后将会得到多少分？

       在这样的一个问题中，前三行（学习1、2、3小时得到相应的分数）是我们的数据集，

       然后我们将数据集传递给算法，经过训练后，得到相应的模型。

       输入第四行的新数据（学习4小时）， 到训练过的模型后， 得到我们预测的结果。这就是机器学习（监督学习）的一整个过程。

      监督学习（Supervised Learning）：前三行属于我们的（Training Set）训练集（x，y） ；                                                                      最后一行属于我们的（Test Set）测试集（x）.

      我们知道训练集里的所有数据，来验证我们训练出来的模型的准确程度, 测试集里的 y 需要我们用模型去算出。

---

 机器学习中容易出现的问题：过拟合

       就是在训练集里训练效果出色，但投入实际应用时，在其他噪声的干扰下，效果不佳。

       为了预防这样的问题，我们将训练集又分成了两个部分，一部分用来训练，另一部分则用来评估，称为开发集（Dev），最后在进行测试。  

        我们应该保证训练出来的模型应该有泛化能力

---

回到上面的问题，我们如何根据上面的问题去针对数据集而设计一个合适的模型呢？

2. 建立一个线型模型

 

  将模型简化，得到ŷ（y_hat ）= x * w

    3   接着机器会进行随机猜测，不同w权重所得到的直线是不一样的，可大可小。

       所以需要我们去评估，当我们取了一个权重之后，它所表示的模型和我们数据集之间的偏移程度有多大：    ŷ(1)-y(1)   、  ŷ (2)-y(2)   、 ŷ(3)-y(3)

      蓝色直线表示的是 ŷ 的值， 红色直线（True Line）表示的是 y 的值。

 3.损失函数（Loss function）

evaluate model  error

我们将评估模型与数据集之间的误差称为损失函数Training Loss（Error）如下：

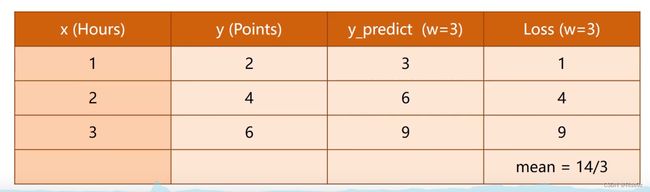
将我们的训练集代入损失函数，得到下面的表格，同时求出他们的平均损失（w=3）

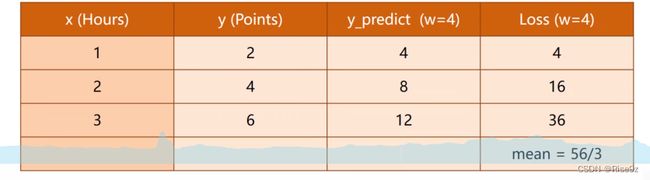
w=4

                                                                           w=2（理想状态）

   通过上面的测试，可以清楚地得知，

   我们的目标，就是要找到当权重取什么样的值，可以使得损失函数取到最小

4.代价函数Cost function

损失函数（Loss Function ）是定义在单个样本上的，算的是一个样本的误差；

而代价函数（Cost Function ）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。

 对所有样本的损失函数求和 再除以 样本总数 = Mean Square Error （平均平方误差）

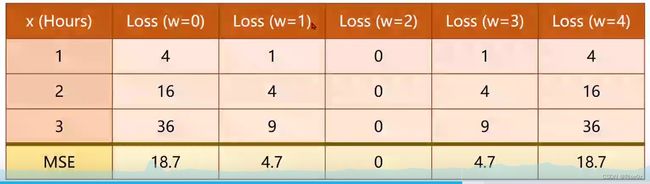
将上面的数据整合到如下的表格：

      然后我们就可以用前面所讲过的穷举法来完成一个线型回归模型。

       经过测试，我们认为权重 w 在0到4之间存在最小的损失函数值，所以把w在0到4之间的取值，都去进行计算损失，求得MSE，我们就可以绘制出如下线型图：

      从图上，我们也可以清楚地知道 w=2时， MSE损失达到最小。

5.运用代码来训练线性模型

我们如何用代码具体进行训练呢？

如下：

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]   # 保存数据集x
y_data = [2.0, 4.0, 6.0]   # y


def forward(x):       # 定义模型前馈
    return x * w


def loss(x, y):       # 定义损失函数
    y_pred = forward(x)
    return(y_pred - y) * (y_pred - y)


w_list = []     # 准备两个空列表
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):    # 生成权重为0.0到4.0序列
    print('w=', w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):  # 调用x、y表格的数据
        y_pred_val = forward(x_val)    # 打印数据并计算预测值
        loss_val = loss(x_val, y_val)    # 计算损失函数
        l_sum += loss_val    # 对损失函数进行求和
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3)    # 转变成MSE并打印
    w_list.append(w)
    mse_list.append(l_sum / 3)

 具体效果如下：

 我们将上面所得到的数据进行绘图：（输入如下代码）

  plt.plot(w_list, mse_list)       # 绘制线性图
    plt.ylabel('Loss')
    plt.xlabel('w')
    plt.show()

得到效果图：