opencv图像处理——图像旋转

图像旋转

1、仿射变换
仿射变换（Affine Transformation或 Affine Map），又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间的过程。它保持了二维图形的“平直性”（即：直线经过变换之后依然是直线）和“平行性”（即：二维图形之间的相对位置关系保持不变，平行线依然是平行线，且直线上点的位置顺序不变）。

2、一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).

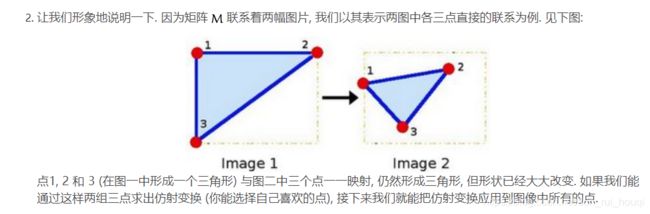
综上所述, 我们能够用仿射变换来表示:

旋转 (线性变换)
平移 (向量加)
缩放操作 (线性变换)
现在可以知道, 事实上, 仿射变换代表的是两幅图之间的 关系 .
而我们通常使用2 x 3的矩阵来表示仿射变换。

最后一列做偏移量

仿射变换矩阵M一般是2*3

在OpenCV中可用函数
C++: Mat getAffineTransform(InputArray src, InputArray dst)来求此矩阵，
InputArray src：表示输入的三个点

InputArray dstL:表示输出的三个点

另一个函数可更方便的求出仿射矩阵M
getRotationMatrix2D(center, angle, scale)

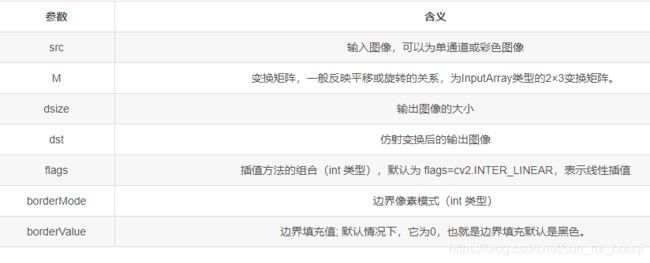
求出仿射变换矩阵后，就可以进行仿射变换；
warpAffine(src, M, dsize, dst, flags, borderMode, borderValue)

void Pixel_Demo::rotate_demo(Mat&image) {
Mat dst, M;
int w = image.rows;
int h = image.cols;
//M 是用来旋转变换相乘的矩阵
M = getRotationMatrix2D(Point2f(w / 2, h / 2), 45, 1.0);//Point2f原图像的中心，旋转角度，缩放比例
/*
M= [cosa sina 0]
[-sina cosa 0]
**/
//如果已知原图和目标图可各取三点，用函数getAffineTransform( srcTri, dstTri )求仿射变换矩阵M
std::cout << M << std::endl;
double cos = abs(M.at(0, 0));
double sin= abs(M.at(0, 1));
int nw = cos*w + sin * h;//新画布的宽
int nh = sin * w + cos * h;//新画布的高
M.at(0, 2) += (nw / 2 - w / 2);//将目标图像移到中心
M.at(1, 2) += (nh / 2 - h / 2);

warpAffine(image, dst, M, Size(nw,nh),INTER_LINEAR,0,Scalar(0,255,0));

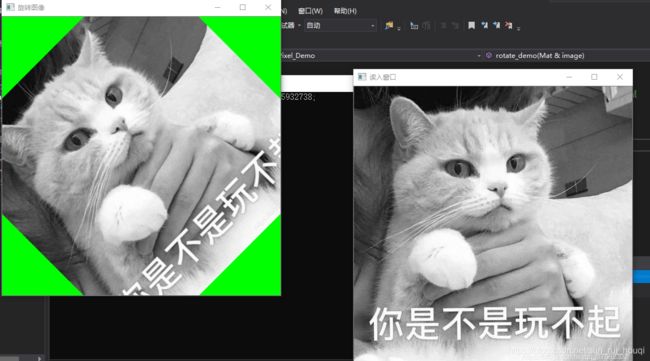
imshow("旋转图像", dst);

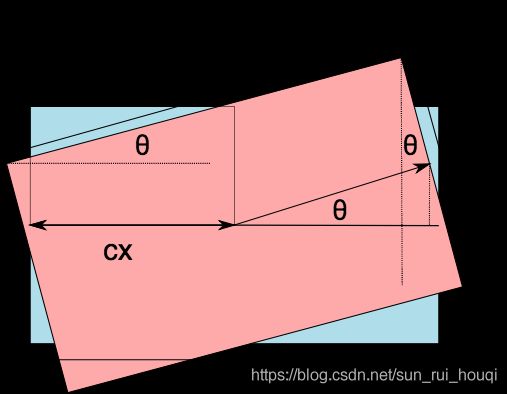
图像旋转后，画布会变大 ，要更新画布：

更新画布：

（M= [cosa sina 0]
[-sina cosa 0]）
double cos = abs(M.at(0, 0));
double sin= abs(M.at(0, 1));
int nw = cos*w + sin * h;//新画布的宽
int nh = sin * w + cos * h;//新画布的高

但是图片不在中心位置：要平移：
M.at(0, 2) += (nw / 2 - w / 2);//将目标图像移到中心
M.at(1, 2) += (nh / 2 - h / 2);