【torch】torch.pairwise_distance分析

every blog every motto: You can do more than you think.

0. 前言

记录torch.pairwise_distance

1. 一维

1.1 元素个数相同

1.1.1 元素个数为1

生成代码:

t = torch.randn(1)
f = torch.randn(1)

计算代码，下同，不重复

dist_matrix = torch.pairwise_distance(t, f)

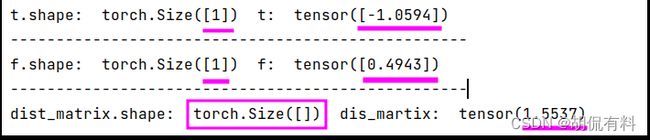
print('t.shape: ', t.shape, ' t: ', t)
print('-' * 50)
print('f.shape: ', f.shape, ' f: ', f)
print('-' * 50)
print('dist_matrix.shape: ', dist_matrix.shape, ' dis_martix: ', dist_matrix)

值为：
$$res=\sqrt{(a-b{)}^2}$$
即：
$$\sqrt{(-1.0594-0.4943{)}^2}=1.5537$$
注意： 输出的维度，0维，即一个标量

1.1.2 元素个数大于1

t = torch.randn(3)
f = torch.randn(3)

计算过程与上述相同，即对应元素相减平方和后再开方

1.2 元素个数不同

1.2.1 第一种情况

t = torch.randn(2)
f = torch.randn(3)

报错如下

1.2.2 第二个情况（其中一个为1）

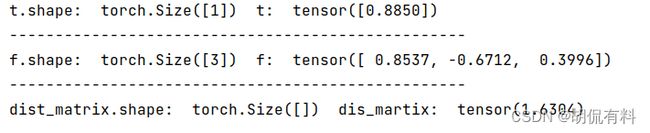
t = torch.randn(1)
f = torch.randn(3)

虽然元素个数不同，但依然可以计算。计算过程：

元素个数为1的元素依次与f中每个元素依次进行之前的计算步骤，即相减平方和后再开方，可自行验证。

说明： 类似进行了numpy中boradcasting操作

1.3 小结

• 元素相同时，对应元素与相减后平方和再开方

• 元素不相同时，其中一个元素个数为1才可进行计算，否则报错

2. 二维

2.1 元素个数相同

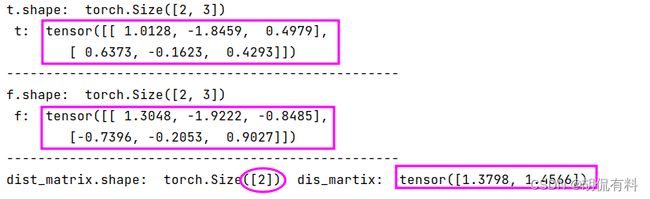
t = torch.randn(2, 3)
f = torch.randn(2, 3)

对输出进行了调整，

最内维的元素与前面的计算过程类似，即，对应元素相减平方和在开方

现在我们的输出维度是2

2.2 维度上元素个数不同

2.2.1 第一维

t = torch.randn(4, 3)
f = torch.randn(2, 3)

t = torch.randn(1, 3)
f = torch.randn(2, 3)

2.2.2 第二维

t = torch.randn(2, 4)
f = torch.randn(2, 3)

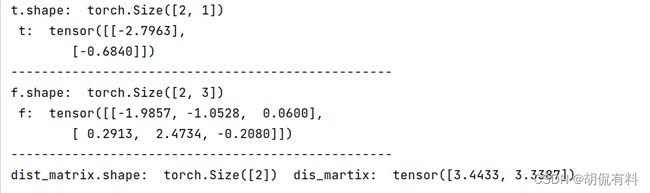
t = torch.randn(2, 1)
f = torch.randn(2, 3)

2.3 小结

• 元素个数相同
  • 最内维（第二维）的计算过程和仅一维的情况计算过程相同
• 维度上元素个数不同
  • 不同时，其中一个元素个数为1方可计算，否则报错

3. 多维

3.1 元素个数相同

t = torch.randn(2, 5, 2, 3)
f = torch.randn(2, 5, 2, 3)

3.2 元素个数不同

3.2.1 非最内维

t = torch.randn(2, 3, 2, 3)
f = torch.randn(2, 5, 2, 3)

t = torch.randn(2, 1, 2, 3)
f = torch.randn(2, 5, 2, 3)

3.2.2 最内维

t = torch.randn(2, 5, 2, 4)
f = torch.randn(2, 5, 2, 3)

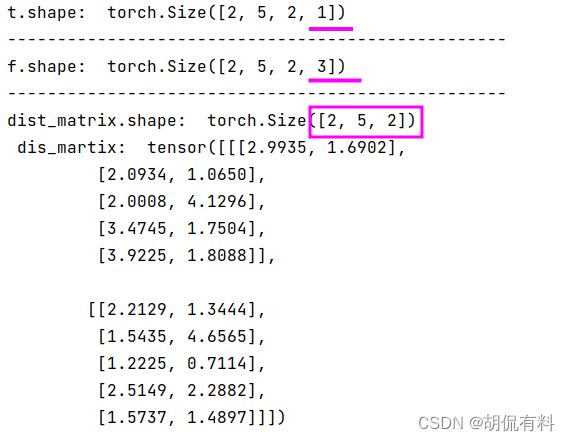
t = torch.randn(2, 5, 2, 1)
f = torch.randn(2, 5, 2, 3)

3.3 小结

同2.3

4. 总结

1. 仅对最后一维进行“计算”，即，相减平方和再开方
2. 不同维度上的维数不同时，需要其中一个为1（进行类似boradcasting操作），才可以计算。
3. 最后一维可以理解为特征，即，计算每一个特征的距离
4. 参考1说是像素级欧式距离计算，笔者感觉不准确。（1）如果是像素级计算，维度不应有改变（对应像素之间有一个距离，计算的结果应该还是一个数，所以维度不变）（2）可参考2

官方案例：

参考

[1] https://blog.csdn.net/qq_36560894/article/details/112199266#commentBox
[2] https://pytorch.org/docs/stable/generated/torch.nn.PairwiseDistance.html#torch.nn.PairwiseDistance