EM算法推导、优缺点及改进方法
EM算法推导
文章目录
- EM算法推导
-
- EM算法内容
-
- EM算法过程
- 算法证明:为什么能用EM算法求最大似然
-
- E-step
- M-step
- 整体过程
- 收敛性证明
-
- 对数似然函数递增
- 有界性
- EM算法的应用
- EM算法优缺点
-
- 优点
- 缺点
- 改进方法
- 参考文献
EM算法内容
概率模型有时既含有观测变量(observable variable),又含有隐变量或潜在变量 (latent variable). 如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计法,或贝叶斯估计法估计模型参数。但是,当模型含有隐变量时,就不能简单地使用这些估计方法。
EM 算法就是含有隐变量的概率模型参数的极大似然估计法,或极大后验概率估计法。
EM算法过程
算法证明:为什么能用EM算法求最大似然
目标是求最大化对数似然函数 ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ)的参数的值:
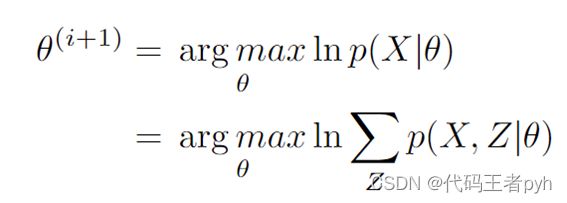
将对数似然函数 ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ)写成 L ( q , θ ) L(q,\theta) L(q,θ)和 K L ( q ∣ ∣ p ) KL (q||p) KL(q∣∣p) 的和:

其中,

等式证明:
根据概率乘积公式


所以,看下图, L ( q , θ ) L(q,\theta) L(q,θ)可以看成对数似然函数 ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ)的下界

E-step
所以在E-step, 让 q ( Z ) = p ( Z ∣ θ o l d ) q(Z) = p(Z|\theta^{old}) q(Z)=p(Z∣θold) , 此时 K L ( q ∣ ∣ p ) = 0 KL(q||p) = 0 KL(q∣∣p)=0 , 因此下界 L ( q , θ ) L(q,\theta) L(q,θ) 被最大化,此时下界和对数似然函数相等,即 L ( q , θ ) = ln p ( X ∣ θ ) L(q,\theta) = \ln p(X|\theta) L(q,θ)=lnp(X∣θ) ,如下图所示

M-step

所以在M-step, 我们寻找参数 θ n e w \theta^{new} θnew 去最大化下界 L ( q , θ ) L(q,\theta) L(q,θ),同时也可以让对数似然函数 ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ)增加,因为我们在E-step中将下界放大到和对数似然函数相等。
然而,最大化 L ( q , θ ) L(q,\theta) L(q,θ) 可以证明等价于最大化 Q ( θ , θ o l d ) Q(\theta,\theta^{old}) Q(θ,θold)
整体过程

在第 i 次迭代的E-step,使得下界 L ( q , θ ) L(q,\theta) L(q,θ) (蓝色曲线)在 θ o l d \theta^{old} θold 处和对数似然函数 ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ) (红色曲线)相等。
在第 i 次迭代的M-step,找到 θ n e w \theta^{new} θnew 最大化 L ( q , θ ) L(q,\theta) L(q,θ) (蓝色曲线)。
在第 i +1次迭代的E-step,使得下界 L ( q , θ ) L(q,\theta) L(q,θ) (蓝色曲线)变到绿色曲线,使得在 θ n e w \theta^{new} θnew 处和对数似然函数 ln p ( X ∣ θ ) \ln p(X|\theta) lnp(X∣θ) (红色曲线)相等。
…
收敛性证明
对数似然函数递增
有界性
所以对数似然有上界 0, ln p ( X ∣ θ ) ≤ 0 \ln p(X|\theta) \le 0 lnp(X∣θ)≤0
因为对数似然函数递增且有上界,所以是收敛的。
EM算法的应用
K-Means
Gaussian Mixture Model (GMM)
Hidden Markov model (HMM) …
EM算法优缺点
优点
- M步只涉及完整数据的最大似然,通常计算起来比较简单。
- 收敛是稳定的,不需要设置任何超参数来使其收敛
缺点
- 对初始值很敏感
- 局部最优解
- 如果数据集非常大,计算量会非常大。
改进方法
Monte Carlo Expectation Maximisation (MCEM)
Expectation/Conditional Maximisation (ECM)
Parameter Expansion Expectation Maximisation (PX-EM)
…
更多改进方法:
-
https://zhuanlan.zhihu.com/p/28372746?utm_source=wechat_session&utm_medium=social&utm_oi=718781202143662080
-
https://www.docin.com/p-2007072095.html?docfrom=rrela
-
https://www.docin.com/p-2344124538.html
参考文献
李航 《统计学习方法》
Bishop, Christopher M. (2006). Pattern recognition and machine learning. New York :Springer,






