基于五等均分法和Bob Stone法衡量RFM顾客价值

最近学习了衡量RFM模型的两种顾客价值的方法，即五等均分法和Bob Stone法。仅以此博客记录我的学习过程，后序学习到了其他方法再来补充。关于RFM实战案例可参考我的其他文章大数据分析案例-基于RFM模型对电商客户价值分析

大数据分析案例-用RFM模型对客户价值分析(聚类)

目录

数据集介绍

 五等均分法

1.给分机制的设计

2.Python代码实现

 Bob Stone法

1.给分机制的设计

 2.Python代码实现

两种方法的比较

---

数据集介绍

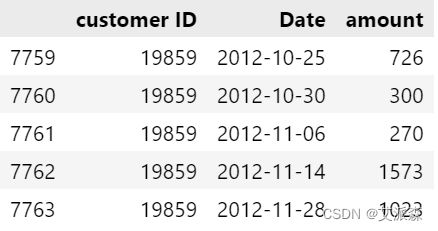
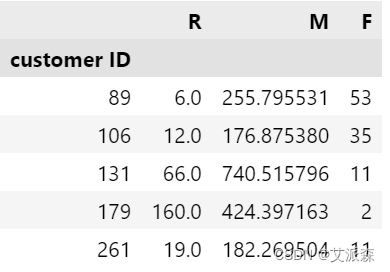
本次实验用的数据的主要是2011-2012年100位客户的信用卡消费记录，数据共有三个字段，顾客ID、消费日期、消费金额，其中的一位客户数据如下： 

 五等均分法

如何综合使用R、F、M三项指标来衡量顾客价值?业界常见的做法是根据客户在三个指标上的排序，转化RFM原始数据成为可合并的分数。首先，将客户的最近购买期间（R）由小到大排序；排序愈靠前的客户代表不久之前才购买，与企业的交易关系仍很密切，因此有较高的顾客价值，得到较高的R分数（R-score）。其次，再按照客户的购买频率（F）由大到小排序，排序在前的客户获得较高的F分数（F-score）。最后，再按照客户的平均购买金额（M）由高到低排序，排序在前的客户获得较高的M分数（M-score）。

1.给分机制的设计

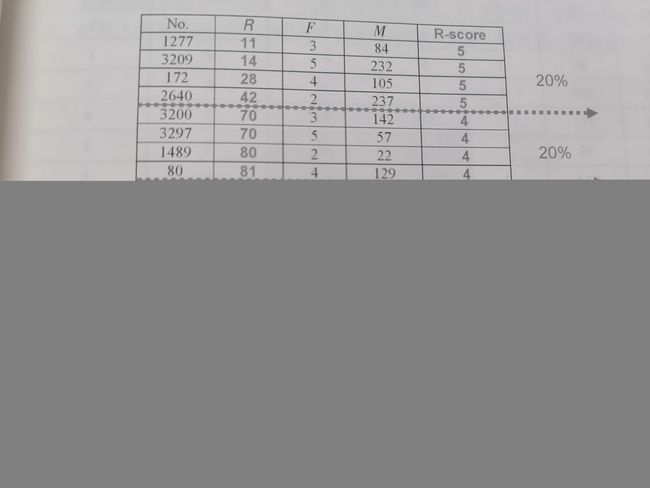
 五等均分法的给分机制是令排序在前20%的客户获得5分，下一个20%的客户获得4分，其余以此类推。图4-2显示客户按照最近购买期间（R）由小到大的排序结果，以及对于的给分结果。例如，编号1277、3209.....等客户的R值最小，因此R分数获得5分。然后，重新按照客户的购买次数（F）由大到小排序，再以20%的人数比例切割成五群，依序给予5、4、3、2、1分。最后，再重新按照客户的平均购买金额（M）由大到小排序，依序给予各群客户适当的M分数。

2.Python代码实现

首先还是导入数据

import pandas as pd
import numpy as np

data = pd.read_excel('data.xlsx')
data.tail() # 查看数据最后五行

接下来就是要构造我们的rfm模型，因为我们这里使用的是国内数据，而这些方法的金额给分机制都是基于美元来设计，所有需要转换一下。 

# 已知美元汇率为7.05
data['amount'] = data['amount'].apply(lambda x:x/7.05)  # 将RMB转换为美元
# 这里类似于Excel中的数据透视表，以客户ID为索引获取最后一次的消费日期，消费次数、平均购买金额
rfm = data.pivot_table(index='customer ID',aggfunc={'Date':'max','customer ID':'count','amount':'mean'})
rfm.head()

然后对上一步进行优化 

rfm.columns = ['R','M','F']
max_dt = pd.to_datetime('2012-12-1')  # 窗口期，即最后的统计日期
rfm['R'] = (max_dt-rfm['R']).values/np.timedelta64(1,'D')
rfm.head()

 

 接下来就需要实现我们的五等均分法了，这里使用pandas中的qcut实现，关于pandas基础知识可参考一文让你快速上手Pandas

# 利用pandas中的qcut来实现五等均分法
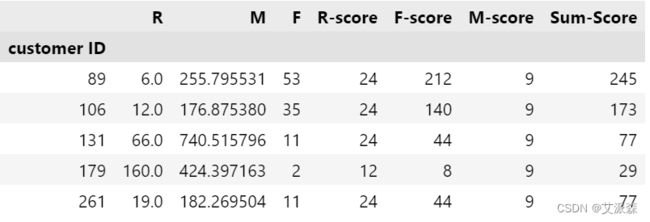
rfm['R-score'] = pd.qcut(rfm['R'],q=5,labels=[5,4,3,2,1])
rfm['M-score'] = pd.qcut(rfm['M'],q=5,labels=[1,2,3,4,5])
rfm['F-score'] = pd.qcut(rfm['F'],q=5,labels=[1,2,3,4,5])
rfm['R-score'] = rfm['R-score'].astype(int)
rfm['M-score'] = rfm['M-score'].astype(int)
rfm['F-score'] = rfm['F-score'].astype(int)
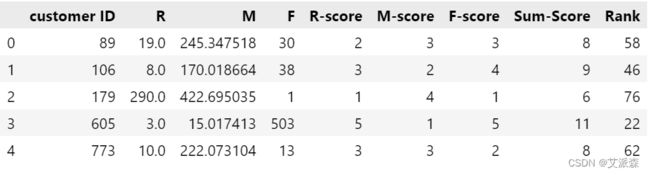
rfm['Sum-Score'] = rfm['R-score'] + rfm['M-score'] + rfm['F-score']
rfm.head()

最后我们可以根据总分进行排序，这一步我是为了不打乱原始客户ID的排序方便后面和Bob Stone法进行对比，所以这里可能稍微多几部操作。

rfm.reset_index(inplace=True)
df1 = rfm[['customer ID','Sum-Score']]
rfm2 = df1.sort_values(by='Sum-Score',ascending=False)
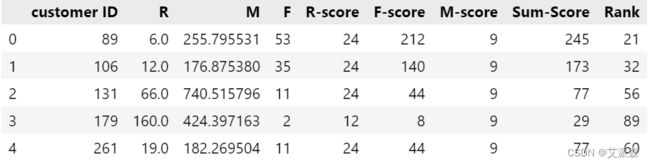
rfm2['Rank'] = [i for i in range(1,len(df1)+1)]
rfm2.drop('Sum-Score',axis=1,inplace=True)
result = pd.merge(rfm,rfm2,on='customer ID')
result.head()

 最后你可以将上面结果保存为Excel文件

result.to_excel('五等均分法.xlsx',index=False)

 Bob Stone法

1.给分机制的设计

根据五等均分法所产生的RFM分数，实质上属于顺序尺度，不适合进行量化分析。因此，Bob Stone（1995）提出另外一种给分机制，将R、F、M等衡量单位不同且数值范围大小有异的三个变量，按照比例尺的概念，转换成简洁的整数，如表4-6所示。例如，最近一次购买期间（R）等比例地切割成最近三个月之内、3~6个月、6~9个月、9~12个月及超过12个月等五个区间，对应的R分数分别是24分、12分、6分、3分、及0分等。代表购买频率高低的F分数，设定为实际购买次数的4倍。代表购买金额多寡的M分数，设定为平均购买金额（以美元计）的10%，再无条件计入为整数，超过9分者以9分计。

 2.Python代码实现

前面准备RFM模型数据的代码跟上面的五等均分法几乎一样

import pandas as pd
import numpy as np
data = pd.read_excel('data.xlsx')
# 已知美元汇率为7.05
data['amount'] = data['amount'].apply(lambda x:x/7.05)
rfm = data.pivot_table(index='customer ID',aggfunc={'Date':'max','customer ID':'count','amount':'mean'})
rfm.columns = ['R','M','F']
max_dt = pd.to_datetime('2012-12-1')
rfm['R'] = (max_dt-rfm['R']).values/np.timedelta64(1,'D')
rfm.head()

接着开始根据给分机制实现Bob Stone法 

def r_score(x):
    if x<=30*3:
        return 24
    elif 30*3

接着还是根据总分进行排序

rfm.reset_index(inplace=True)  # 还原rfm的索引列customer ID
df1 = rfm[['customer ID','Sum-Score']]
rfm2 = df1.sort_values(by='Sum-Score',ascending=False)
rfm2['Rank'] = [i for i in range(1,len(df1)+1)]  # 根据总分进行排名
rfm2.drop('Sum-Score',axis=1,inplace=True)
result = pd.merge(rfm,rfm2,on='customer ID') 
result.head()

 最后可以将上面结果保存为Excel文件

result.to_excel('Bob Stone法.xlsx',index=False)

两种方法的比较

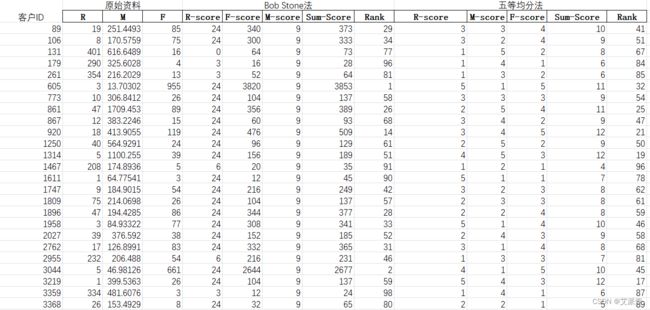
前面我们已经实现了两种方法，接着我们可以手动进行整理如下所示：

 由表可知，两种给分法的计算结果差异颇大。例如，ID为605的客户的顾客价值在Bob Stone法下是第1名，但是在五等均分法下却是第32名。那么，对于这家银行企业而言，给分机制究竟要如何设定，RFM分数才能有效地反映顾客价值的高低呢？以RFM给分机制为例，企业可以通过样本的切割与对比，去评估何种参数设定具有最高信度，以此计算顾客价值。

所以，针对上述问题，这里我们将原始两年数据进行切半，令前一年数据为建模样本，后一年数据为验证样本，如图4-7所示，获得客户分别在建模样本与验证样本下的顾客价值顺序。然后计算两者的顺序相关系数，系数愈靠近1则代表Bob Stone法的信誉度愈高，愈适合以过去的RFM分数去预测未来的顾客价值，也代表愈合作为顾客价值的给分机制。

我们先使用五等均分法，并计算其顺序相关系数。

关于划分数据，只需要在前面代码读取完数据后添加一下年份筛选即可，代码如下：

data = data[data['Date'].dt.year==2011]
# data = data[data['Date'].dt.year==2012]

可视化并计算相关系数代码如下： 

import pandas as pd
import matplotlib.pylab as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #解决中文显示
plt.rcParams['axes.unicode_minus'] = False   #解决符号无法显示
def main():
    rank_list = []
    for year in [2011,2012]:
        data1 = pd.read_excel(f'五等均分法-{year}.xlsx',usecols=['客户ID','Sum-Score'])
        df1 = data1.copy()
        df2 = df1.sort_values(by='Sum-Score',ascending=False)
        df2['Rank'] = [i for i in range(1,len(df1)+1)]  # 根据总分进行排名
        df2.drop('Sum-Score',axis=1,inplace=True)
        result = pd.merge(data1,df2,on='客户ID') 
        rank = result['Rank'].values.tolist()
        rank_list.append(rank)
        result.to_excel(f'五等均分法-{year}.xlsx')

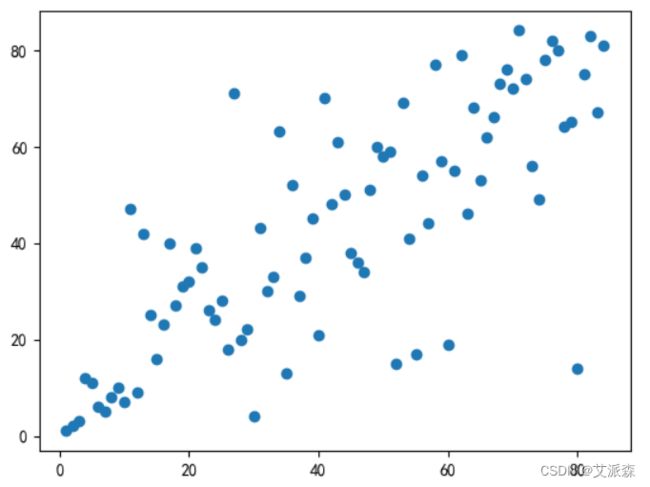
    plt.scatter(rank_list[0],rank_list[1])  # 可视化
    plt.show()
    res = pd.DataFrame()
    res['rank1'] = rank_list[0]
    res['rank2'] = rank_list[1]
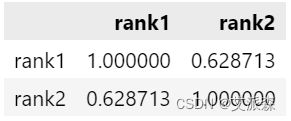
    print(res.corr())  # 打印相关系数

main()

 

从结果看出，五等均分法的顺序相关系数为0.6287。

接着我们算Bob Stone法的相关系数，跟上面代码一样，只不过把数据换下。最后结果如下：

 

从结果我们看出Bob Stone法的顺序相关系数为0.7656明显高于五等均分法，所有愈适合以过去的RFM分数去预测未来的顾客价值，也愈合适合作为顾客价值的给分机制。