【数学建模】青少年犯罪问题 | 逐步回归分析法stepwise函数 | 残差分析rcoplot

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、逐步回归分析法

1.1.逐步回归分析定义，最优回归方程

逐步回归分析（stepwise regression analysis），选择自变量以建立最优回归方程的回归分析方法。最优回归方程，指在回归方程中，包含所有对因变量有显著影响的自变量，而不包含对因变量影响不显著的自变量。过程是：按自变量对因变量影响效应，由大到小逐个把有显著影响的自变量引入回归方程，而那些对因变量影响不显著的变量则可能被忽略。另外，已被引入回归方程的变量在引入新变量后，其重要性可能会发生变化，当效应不显著时，则需要从回归方程中将此变量剔除。引入一个变量或从回归方程中剔除一个变量都称为逐步回归的一步。每一步都要进行F检验，以保证在引入新变量前回归方程中只含有对因变量影响显著的变量，而不显著的变量已被剔除。直到回归方程中所有变量都不能剔除而又没有新变量可以引入时为止，逐步回归过程结束。实际应用时，需要注重逐步回归分析跟自己研究假设之间的关联。由于运算过程比较复杂，可通过统计软件中的回归分析模块进行（从百度抄的的定义）

简单的说，就是探究自变量对因变量的影响，有些自变量对因变量影响大，有些影响小。

1.2.stepwise函数介绍

stepwise（X，y）属于比较常用的调用格式，其中X是自变量数据，是一个矩阵。y是因变量，是一个列向量。inmodel表示矩阵列数的指标，缺省时设定为全部自变量；

二、例题：青少年犯罪问题

2.1.题目简述

2.2.问题一建模与求解

2.2.1 只存在两个因素时

首先拿到一组数据，我们首先画出他们的x-y图像，看看可能存在的关系。
代码如下（示例）：

clc;
clear;
%自变量1：低收入家庭百分比
x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 ... 
    18.1 23.1 19.1 24.7 18.6 24.9 17.9 22.4 20.2 16.9]; 
%自变量2：失业率
x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 ...
    6.0 7.4 5.8 8.6 6.5 8.3 6.7 8.6 8.4 6.7]; 
%自变量3：总人口数
x3=[587 643 635 692 1248 643 1964 1531 713 749 ...
    7895 762 2793 741 625 854 716 921 595 3353];
%因变量：犯罪率
y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 ...
   14.5 26.9 15.7 36.2 18.1 28.9 14.9 25.8 21.7 25.7]; 
figure(1),plot(x1,y,'o'); 
xlabel('低收入家庭百分比'); ylabel('犯罪率');
figure(2),plot(x2,y,'o'); 
xlabel('失业率'); ylabel('犯罪率');
figure(3),plot(x3,y,'o'); 
xlabel('总人口数（千人）'); ylabel('犯罪率');

最后生成的结果如下：



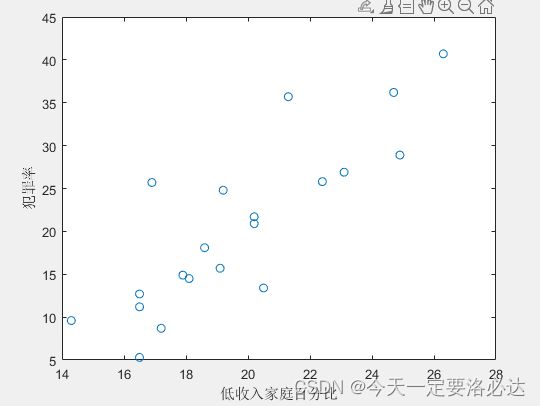
可以模糊看出，自变量1和自变量2和因变量存在一定“线性”关系，自变量3看不出来。
接下来进行逐步回归分析,这里考虑简单一点，只考虑 x1,x2,x3三个自变量存在的可能性，不考虑x1x2,x1x3,x2x3,x1^2等：（我只是想偷懒）

X=[x1',x2',x3']; %使用stepwise函数时，将自变量数据转置后组成矩阵
stepwise(X,y)

得到结果如下：

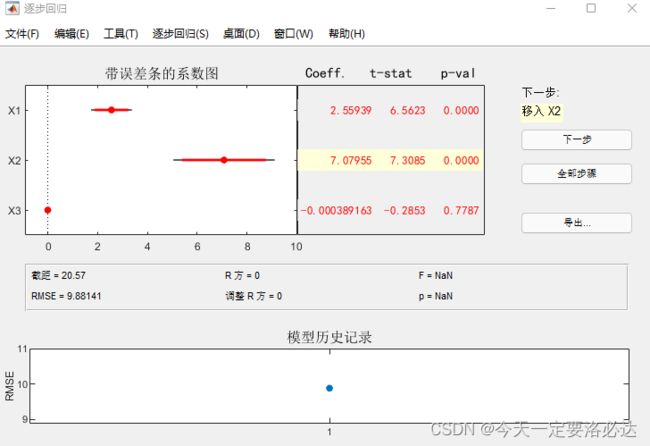
操作这张图就能得到很多有效信息。可以点击“全部步骤”做完所有分析，也可以点击“下一步”一步步来。
图中最重要的信息是：Coeff（回归系数），截距，RMSE
RMSE越小，说明这个方法下模型越合理
下面看下操作就懂了。

当x1,x2成为自变量时（点击x1,x2那两条，蓝色即是被选中）

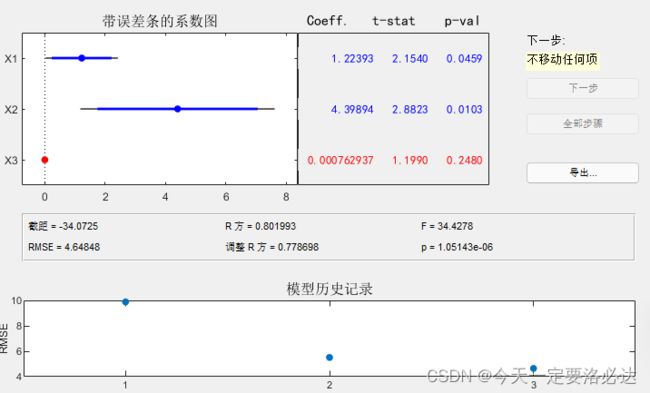
此时回归方程为y=-34.0725+1.22393x1+4.39894x2

当x2,x3成为自变量时（点击x2,x3那两条）

此时回归方程为y=-31.5996+7.35187x2+0.000826627x3

当x1,x3成为自变量时（点击x1,x3那两条）

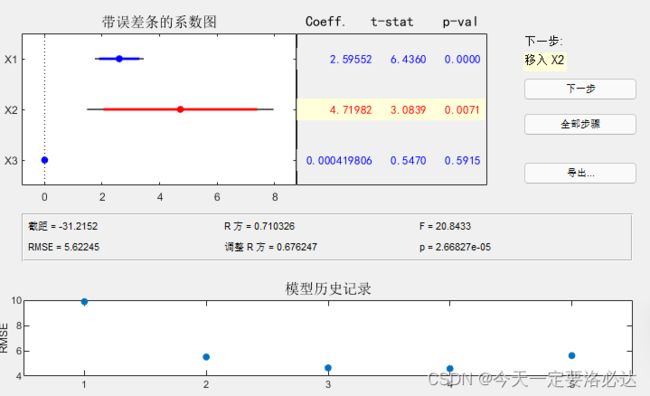
此时回归方程为y=-31.2152+2.59552x1+0.000419806x3

通过以上结果可以看到，x1,x2是自变量的时候，RMSE最小，为最优。
其中模型历史记录可以看到历次操作后的RMSE值：

2.2.2 存在三个因素时

紧接着刚刚的逐步回归分析，如果我们把三个自变量都选中：

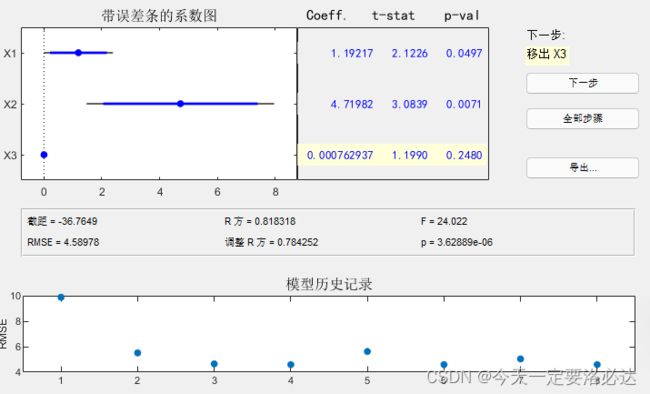
可以看出，x3的回归系数很小，几乎为0，没啥用（此时工具箱也让我们移除x3），这时候我们考虑一下x1x2,x1x3,x2x3,x1^2等存在的可能性

X1=[x1',x2',x3',(x1.*x2)',(x2.*x3)',(x1.*x3)',x1'.^2,x2'.^2,x3'.^2]; 
stepwise(X1,y)

最后得到RMSE最小时（x1,x3,x2x3）：

此时回归方程为y=-13.7725+1.47538x1±0.0314395x3+0.00530496x2x3

2.3.问题二建模与求解

既然题目中说到了改进，比如剔除异常点，那我们就只剔除异常点吧（偷懒…）
检测回归的异常点，这不就是rcoplot函数的工作嘛。

2.3.1 rcoplot函数

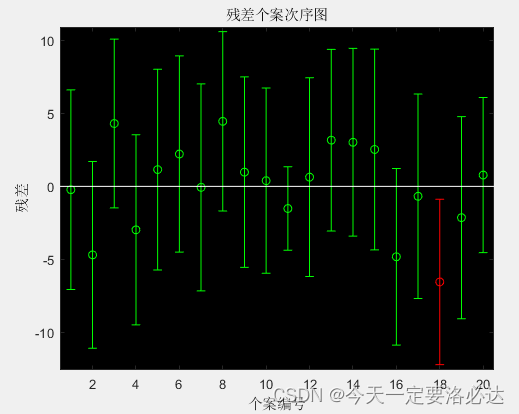
rcoplot(r,rint)函数可以画出回归分析后的残差图，能辨别异常点（残差过大的点，红色的）。r是残差。一般和regress（）一起使用。

2.3.2 解题

在数据代码后加上下面几句：

X2=[ones(20,1),x1',x2']; %回归的因子 1,x1,x2
[b,bint,r,rint,s]=regress(y',X2); %回归分析
rcoplot(r,rint)  %残差分析

结果如下：

很明显第8组数据和18组数据出问题，应该剔除。

我们再看下三个因素时的情况：

X2=[ones(20,1),x1',x3',(x2.*x3)'];
[b,bint,r,rint,s]=regress(y',X2);
rcoplot(r,rint)

18组数据出问题，应该剔除。