宋浩概率论与数理统计笔记——第二章
2.1随机变量的概念
随机变量(random variable)表示随机试验各种结果的实值单值函数。
定义: Ω \Omega Ω样本空间, X = X ( ω ) X=X(\omega) X=X(ω)是 ω \omega ω上的实值函数(每个样本都对应一个数)
随机变量常用 X 、 Y 、 Z 、 ξ 、 η 、 ζ X、Y、Z、\xi、\eta、\zeta X、Y、Z、ξ、η、ζ表示
{ ω ∣ X ( ω ) = a } \{\omega|X(\omega)=a\} {ω∣X(ω)=a}:事件,简写成 { X = a } \{X=a\} {X=a},概率表示为 P { X = a } P\{X=a\} P{X=a}或 P ( X = a ) P(X=a) P(X=a)
例:公交车站每五分钟发一辆车,候车时间 X ∈ [ 0 , 5 ] X\in[0,5] X∈[0,5]
P { x ≥ 0 } = 1 P{\{x\geq0\}}=1 P{x≥0}=1
P { x > 6 } = 0 P\{x>6\}=0 P{x>6}=0
基本类型:
离散型:有限个,无限可列个( 例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。 )
非离散型:连续型( 例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。 )
2.2.1离散型随机变量及其概率分布
概率分布表
| 事件X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 概率P | 1 6 \frac{1}{6} 61 | 1 6 \frac{1}{6} 61 | 1 6 \frac{1}{6} 61 | 1 6 \frac{1}{6} 61 | 1 6 \frac{1}{6} 61 | 1 6 \frac{1}{6} 61 |
| 事件X | 1 | 0 |
|---|---|---|
| 概率P | 1 2 \frac{1}{2} 21 | 1 2 \frac{1}{2} 21 |
X的所有取值 x k ( k = 1 , 2 , . . . ) x_k(k=1,2,...) xk(k=1,2,...)可列个
P { X = x k } = P k P\{X=x_k\}=P_k P{X=xk}=Pk概率函数(分布)
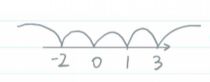
概率函数图
各条线段的总长度相加为1
| X | 2 | 4 | 8 | 16 | 32 | … |
|---|---|---|---|---|---|---|
| P | 1 2 \frac{1}{2} 21 | 1 4 \frac{1}{4} 41 | 1 8 \frac{1}{8} 81 | 1 16 \frac{1}{16} 161 | 1 32 \frac{1}{32} 321 | … |
例:
五个黑球,三个白球,每次抽一个,不放回
直到取到黑球为止,X为取到的白球数目
求 P { − 1 < x < 0 } P\{-1
X = 0 X=0 X=0 P { X = 0 } = 5 8 P\{X=0\}=\frac{5}{8} P{X=0}=85
X = 1 X=1 X=1 P { X = 1 } = 3 8 × 5 7 = 15 56 P\{X=1\}=\frac{3}{8}\times\frac{5}{7}=\frac{15}{56} P{X=1}=83×75=5615
X = 2 X=2 X=2 P { X = 2 } = 3 8 × 2 7 × 5 6 = 5 56 P\{X=2\}=\frac{3}{8}\times\frac{2}{7}\times\frac{5}{6}=\frac{5}{56} P{X=2}=83×72×65=565
X = 3 X=3 X=3 P { X = 3 } = 3 8 × 2 7 × 1 6 × 5 5 = 1 56 P\{X=3\}=\frac{3}{8}\times\frac{2}{7}\times\frac{1}{6}\times\frac{5}{5}=\frac{1}{56} P{X=3}=83×72×61×55=561
| X | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 5 8 \frac{5}{8} 85 | 15 56 \frac{15}{56} 5615 | 5 56 \frac{5}{56} 565 | 1 56 \frac{1}{56} 561 |
P { − 1 < x < 0 } = 0 P\{-1
P { 1 < x < 3 } = 5 56 P\{1
P { x ≤ 3 } = 1 P\{x\leq 3\}=1 P{x≤3}=1
2.2.2分布函数的定义
分布函数对离散型和连续型都是成立的
定义:设 X X X位一随机变量,则对任意实数 x x x, { X ≤ x } \{X\leq x\} {X≤x}是一个随机事件,称
F ( x ) = P { X ≤ x } F(x)=P\{X\leq x\} F(x)=P{X≤x}为随机变量 X X X的分布函数
定义域 x ∈ ( − ∞ , + ∞ ) x\in(-\infty,+\infty) x∈(−∞,+∞)
值域 F ( x ) ∈ [ 0 , 1 ] F(x)\in [0,1] F(x)∈[0,1]
X X X的取值不超过 x x x的概率
性质:
1) 0 ≤ F ( x ) ≤ 1 , F ( x ) ∈ [ 0 , 1 ] 0\leq F(x)\leq 1,F(x)\in [0,1] 0≤F(x)≤1,F(x)∈[0,1]
2) F ( x ) F(x) F(x)不减, x 1 < x 2 x_1
lim x → + ∞ F ( x ) = F ( + ∞ ) = 1 \lim_{x\rightarrow +\infty}F(x)=F(+\infty)=1 x→+∞limF(x)=F(+∞)=1
lim x → − ∞ F ( x ) = F ( − ∞ ) = 0 \lim_{x\rightarrow -\infty}F(x)=F(-\infty)=0 x→−∞limF(x)=F(−∞)=0
上面两个公式可用来求参数
3) F ( x ) F(x) F(x)是右连续的,且至多有可列个间断点
- 离散型 右连续
- 连续型 连续
右 连 续 : lim x → a + F ( x ) = F ( a ) 右连续:\lim_{x\rightarrow a^+}F(x)=F(a) 右连续:x→a+limF(x)=F(a)
左 连 续 : lim x → a − F ( x ) = F ( a ) 左连续:\lim_{x\rightarrow a^-}F(x)=F(a) 左连续:x→a−limF(x)=F(a)
连 续 : lim x → a F ( x ) = F ( a ) 连续:\lim_{x\rightarrow a}F(x)=F(a) 连续:x→alimF(x)=F(a)
连续简单来说就是极限值等于函数值
下面的公式对离散型和连续型都是成立的
F ( x ) = P ( X ≤ x ) F(x)=P(X\leq x) F(x)=P(X≤x)
P { x ≤ a } = F ( a ) P\{x\leq a\}=F(a) P{x≤a}=F(a)
P { x > a } = 1 − P { x ≤ a } = 1 − F ( a ) P\{x> a\}=1-P\{x\leq a\}=1-F(a) P{x>a}=1−P{x≤a}=1−F(a)
P { a < x ≤ b } = P { x ≤ b } − P { x ≤ a } = F ( b ) − F ( a ) P\{a
P { x = a } = F ( a ) − F ( a − 0 ) P\{x= a\}=F(a)-F(a-0) P{x=a}=F(a)−F(a−0) ∗ ∗ 注 : F ( a − 0 ) 表 示 不 包 含 x = a 那 个 点 的 区 间 , F ( a ) 表 示 包 含 x = a 那 个 点 的 区 间 **注:F(a-0)表示不包含x=a那个点的区间,F(a)表示包含x=a那个点的区间 ∗∗注:F(a−0)表示不包含x=a那个点的区间,F(a)表示包含x=a那个点的区间
P { a ≤ x ≤ b } = F ( b ) − F ( a − 0 ) P\{a\leq x\leq b\}=F(b)-F(a-0) P{a≤x≤b}=F(b)−F(a−0)
P { x < a } = F ( a − 0 ) P\{ x
P { x ≥ a } = 1 − F ( a − 0 ) P\{x\geq a\}=1-F(a-0) P{x≥a}=1−F(a−0)
例:
F ( x ) = { a − e − λ x x > 0 0 x ≤ 0 F(x) = \left\{ \begin{array}{rcl} a-e^{-\lambda x} & x > 0 \\ 0 & x \leq 0 \end{array}\right. F(x)={a−e−λx0x>0x≤0
λ > 0 , 求 a \lambda > 0,求a λ>0,求a
F ( − ∞ ) = 0 = 0 F(-\infty) = 0=0 F(−∞)=0=0
F ( + ∞ ) = lim x → + ∞ ( a − 1 e λ x ) = lim x → + ∞ ( a − 0 ) = 1 F(+\infty) = \lim_{x\rightarrow +\infty}(a-\frac{1}{e^\lambda x})=\lim_{x\rightarrow +\infty}(a-0)=1 F(+∞)=limx→+∞(a−eλx1)=limx→+∞(a−0)=1
∴ a = 1 \therefore a=1 ∴a=1
2.2.2离散型的分布函数
例:
| X | -1 | 2 | 3 |
|---|---|---|---|
| P | 1 2 \frac{1}{2} 21 | 1 3 \frac{1}{3} 31 | 1 6 \frac{1}{6} 61 |
F ( x ) = P ( X ≤ x ) F(x)=P(X\leq x) F(x)=P(X≤x)
x ∈ ( − ∞ , + ∞ ) x\in(-\infty,+\infty) x∈(−∞,+∞)
解:
x < − 1 x<-1 x<−1 F ( − 1 ) = P ( X ≤ − 1 ) = 0 F(-1) = P(X\leq -1)=0 F(−1)=P(X≤−1)=0
− 1 ≤ x < 2 -1\leq x<2 −1≤x<2 F ( x ) = P ( X ≤ x ) = F ( X = − 1 ) = 1 2 F(x)=P(X\leq x)=F(X=-1)=\frac{1}{2} F(x)=P(X≤x)=F(X=−1)=21
2 ≤ x < 3 2\leq x<3 2≤x<3 F ( x ) = P ( X ≤ x ) = F ( X = − 1 ) + F ( X = 2 ) = 5 6 F(x)=P(X\leq x) = F(X=-1)+F(X=2)=\frac{5}{6} F(x)=P(X≤x)=F(X=−1)+F(X=2)=65
$ x\geq 3$ F ( x ) = P ( X ≤ x ) = F ( X = − 1 ) + F ( X = 2 ) + F ( X = 3 ) = 1 F(x)=P(X\leq x) = F(X=-1)+F(X=2)+F(X=3)=1 F(x)=P(X≤x)=F(X=−1)+F(X=2)+F(X=3)=1
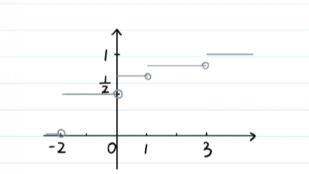
∴ F ( x ) = { 0 x < − 1 1 2 − 1 ≤ x < 2 5 6 2 ≤ x < 3 1 x ≥ 3 \therefore F(x) = \left\{ \begin{array}{rcl} 0 & x < -1 \\ \frac{1}{2} & -1\leq x < 2 \\ \frac{5}{6} & 2\leq x < 3 \\ 1 & x\geq 3 \end{array}\right. ∴F(x)=⎩⎪⎪⎨⎪⎪⎧021651x<−1−1≤x<22≤x<3x≥3
例:
| X | -2 | 0 | 1 | 3 |
|---|---|---|---|---|
| P | 1 2 \frac {1}{2} 21 | 1 4 \frac{1}{4} 41 | 1 8 \frac{1}{8} 81 | 1 8 \frac{1}{8} 81 |
解:
②
x < − 2 x<-2 x<−2
− 2 ≤ x < 0 -2\leq x< 0 −2≤x<0
0 ≤ x < 1 0\leq x<1 0≤x<1
1 ≤ x < 3 1\leq x< 3 1≤x<3
3 ≤ x 3\leq x 3≤x
③
F ( x ) = 0 F(x) = 0 F(x)=0
F ( x ) = 1 2 F(x) = \frac{1}{2} F(x)=21
F ( x ) = 1 2 + 1 4 F(x)=\frac{1}{2}+\frac{1}{4} F(x)=21+41
F ( x ) = 1 2 + 1 4 + 1 8 F(x)=\frac{1}{2}+\frac{1}{4}+\frac{1}{8} F(x)=21+41+81
F ( x ) = 1 2 + 1 4 + 1 8 + 1 8 F(x)=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8} F(x)=21+41+81+81
根据函数值求概率函数:
x k 是 X 的 取 值 x_k是X的取值 xk是X的取值
P { X = x p } = F ( x k ) − F ( x k − 0 ) P\{X = x_p\}=F(x_k)-F(x_k-0) P{X=xp}=F(xk)−F(xk−0)
注 : F ( x k − 0 ) 是 把 F ( x k ) 的 点 往 左 挪 一 点 点 注:F(x_k-0)是把F(x_k)的点往左挪一点点 注:F(xk−0)是把F(xk)的点往左挪一点点
2.2.2连续型的分布函数
$F(x)=P{X\leq x}=\int_{-\infty}^xf(t)dt $
F ′ ( x ) = f ( x ) F'(x)=f(x) F′(x)=f(x)
例:
求 f ( x ) = 1 π ( 1 + x 2 ) f(x)=\frac{1}{\pi(1+x^2)} f(x)=π(1+x2)1的分布函数
F ( x ) = ∫ − ∞ x 1 π ( 1 + t 2 ) d t = 1 π arctan t ∣ − ∞ x = 1 π arctan x + 1 2 F(x)=\int_{-\infty}^x\frac{1}{\pi (1+t^2)}dt=\frac{1}{\pi}\arctan t|_{-\infty}^x = \frac{1}{\pi}\arctan x+\frac{1}{2} F(x)=∫−∞xπ(1+t2)1dt=π1arctant∣−∞x=π1arctanx+21
例:
F ( x ) = { − 1 2 x + 1 0 ≤ x ≤ 2 0 其 他 F(x) = \left\{ \begin{array}{rcl} -\frac{1}{2}x+1 & 0 \leq x \leq 2 \\ 0 & 其他 \end{array}\right. F(x)={−21x+100≤x≤2其他
x < 0 时 , F ( x ) = ∫ − ∞ x 0 d x = 0 x<0时,F(x)=\int_{-\infty}^x0dx=0 x<0时,F(x)=∫−∞x0dx=0
0 ≤ x < 2 时 , F ( x ) = ∫ − ∞ x f ( t ) d t = ∫ − ∞ 0 0 d t + ∫ 0 x ( − 1 2 t + 1 ) d t = − 1 4 x 2 + x 0\leq x<2时,F(x)=\int_{-\infty}^{x}f(t)dt=\int_{-\infty}^{0}0dt+\int_0^x(-\frac{1}{2}t+1)dt=-\frac{1}{4}x^2+x 0≤x<2时,F(x)=∫−∞xf(t)dt=∫−∞00dt+∫0x(−21t+1)dt=−41x2+x
x ≥ 2 时 , F ( x ) = ∫ − ∞ x f ( t ) d t = ∫ − ∞ 0 0 d t + ∫ 0 2 ( − 1 2 t + 1 ) d t + ∫ 2 x 0 d t = 1 x\geq2时,F(x)=\int_{-\infty}^xf(t)dt=\int_{-\infty}^{0}0dt+\int_{0}^{2}(-\frac{1}{2}t+1)dt+\int_{2}^{x}0dt=1 x≥2时,F(x)=∫−∞xf(t)dt=∫−∞00dt+∫02(−21t+1)dt+∫2x0dt=1
例:
F ( x ) = { 0 x < 0 A x 2 0 ≤ x ≤ 1 1 1 ≤ x F(x) = \left\{ \begin{array}{rcl} 0 & x <0 \\ Ax^2 & 0\leq x\leq 1 \\ 1 & 1\leq x \end{array}\right. F(x)=⎩⎨⎧0Ax21x<00≤x≤11≤x
①求A
lim x → 0 + A x 2 = 0 = F ( 0 ) = 0 \lim_{x\rightarrow0^+}Ax^2=0=F(0)=0 limx→0+Ax2=0=F(0)=0
lim x → 1 − A x 2 = A = F ( 1 ) = 1 \lim_{x\rightarrow1^-}Ax^2=A=F(1)=1 limx→1−Ax2=A=F(1)=1
②
F ( x ) = { 2 x 0 ≤ x < 1 0 其 他 F(x) = \left\{ \begin{array}{rcl} 2x & 0 \leq x <1 \\ 0 & 其他 \end{array}\right. F(x)={2x00≤x<1其他
③
P { 0.3 < X < 0.7 } = F ( 0.7 ) − F ( 0.3 ) = 0.4 P\{0.3
2.2.2连续型随机变量及其概率密度函数
引例:
身高150~200
范围 频数
150~160 10
160~170 20
170~180 40
180~190 15
190~200 15
例:有99年的降水量
范围 频数 频率
670~770 1 0.01
770~870 8 0.081
870~970 9 0.091
… … …
1570~1670 3 0.03
频数直方图
频率密度直方图
频率密度直方图的特点
-
每个小长方形的面积等于该组的概率
-
所有的小长方形面积之和等于1
-
介于x=a,x=b之间的面积近似等于(a,b]的概率
当组距很小时,接近于光滑的线,称为概率密度函数
定义:非负可积函数 f ( x ) f(x) f(x), a ≤ b a\leq b a≤b, P { a < x ≤ b } = ∫ a b f ( x ) d x P\{a
x x x:连续型随机变量
f ( x ) f(x) f(x):概率分布密度函数,记作 X ∼ f ( x ) X\sim f(x) X∼f(x)
- f ( x ) ≥ 0 f(x)\geq0 f(x)≥0
- ∫ − ∞ + ∞ f ( x ) = 1 \int_{-\infty}^{+\infty}f(x)=1 ∫−∞+∞f(x)=1(常用来求参数)
- 连续型随机变量取个别值的概率为0
0 ≤ P { x = x 0 } ≤ P { x 0 − Δ x < x ≤ x 0 } = ∫ x 0 − Δ x x 0 f ( x ) d x = 0 0\leq P\{x=x_0\}\leq P\{x_0-\Delta x
连续型,有无端点无所谓:
P { a ≤ x ≤ b } = P { a < x ≤ b } = P { a ≤ x < b } = P { a < x < b } P\{a\leq x\leq b\}=P\{a
P { x < a } = P { x ≤ a } P\{x
P { x > a } = P { x ≥ a } P\{x>a\}=P\{x\geq a\} P{x>a}=P{x≥a}
概率为0的事件未必是不可能事件,概率为1的事件未必是必然事件
例:
KaTeX parse error: Undefined control sequence: \mbox at position 66: …\leq 2 \\ 0 & \̲m̲b̲o̲x̲{其他} \end{arra…
求k
∫ − ∞ + ∞ f ( x ) d x = ∫ 0 2 ( k x + 1 ) d x = 1 2 k x 2 + x ∣ 0 2 = 1 \int_{-\infty}^{+\infty}f(x)dx=\int_{0}^{2}(kx+1)dx=\frac{1}{2}kx^2+x|_0^2=1 ∫−∞+∞f(x)dx=∫02(kx+1)dx=21kx2+x∣02=1
k = − 1 2 k=-\frac{1}{2} k=−21
P { x ≤ 2 } = ∫ − ∞ 2 f ( x ) d x = ∫ 0 2 f ( x ) d x = 1 P\{x\leq 2\}=\int_{-\infty}^{2}f(x)dx=\int_{0}^{2}f(x)dx=1 P{x≤2}=∫−∞2f(x)dx=∫02f(x)dx=1
P { 1.5 < x < 2.5 } = ∫ 1.5 2.5 f ( x ) d x = ∫ 1.5 2 f ( x ) d x = 0.0625 P\{1.5
概率密度函数
在该点的函数值反映了: X X X取 x x x附近值的大小, P { x < X < x + Δ x } P\{x
lim Δ x → 0 P { x < X < x + Δ x } Δ x = lim Δ x → 0 ∫ x x + Δ x f ( x ) d x Δ x = f ( x ) \lim_{\Delta x\rightarrow 0}\frac{P\{x
P { x < X < x + Δ x } ≈ f ( x ) Δ x P\{x
2.2.3 正态分布
ϕ ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 \phi(x) = \frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{(x-\mu)^2}{2{\sigma}^2}} ϕ(x)=2πσ1e−2σ2(x−μ)2, − ∞ < x < + ∞ -\infty< x < +\infty −∞<x<+∞
X X X~ N ( μ , σ 2 ) N(\mu,\sigma ^2) N(μ,σ2)
∫ − ∞ + ∞ e − x 2 d x = π \int_{-\infty}^{+\infty}e^{-x^2}dx = \sqrt{\pi} ∫−∞+∞e−x2dx=π
1 2 π σ ∫ − ∞ + ∞ e − ( x − μ 2 σ ) 2 d ( x − μ 2 σ ) = 1 π × π = 1 \frac{1}{\sqrt{2\pi} \sigma}\int_{-\infty}^{+\infty}e^{-(\frac{x-\mu}{\sqrt{2}\sigma})^2}d(\frac{x-\mu}{\sqrt{2}\sigma}) = \frac{1}{\sqrt{\pi}}\times\sqrt{\pi} = 1 2πσ1∫−∞+∞e−(2σx−μ)2d(2σx−μ)=π1×π=1
分布函数:
Φ ( x ) = 1 2 π σ ∫ − ∞ x e − ( t − μ ) 2 2 σ 2 d t \Phi(x) = \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}e^{-\frac{(t-\mu)^2}{2\sigma ^2}}dt Φ(x)=2πσ1∫−∞xe−2σ2(t−μ)2dt
性质:
-
y = φ ( x ) y=\varphi(x) y=φ(x)以 x = μ x=\mu x=μ为对称轴,钟形曲线
x = μ x=\mu x=μ时 φ ( x ) \varphi(x) φ(x)最大值 1 2 π σ \frac{1}{\sqrt{2\pi}\sigma} 2πσ1
-
y = φ ( x ) y=\varphi(x) y=φ(x)以 x x x轴为渐近线且在 x = μ ± σ x=\mu \pm \sigma x=μ±σ处有拐点
-
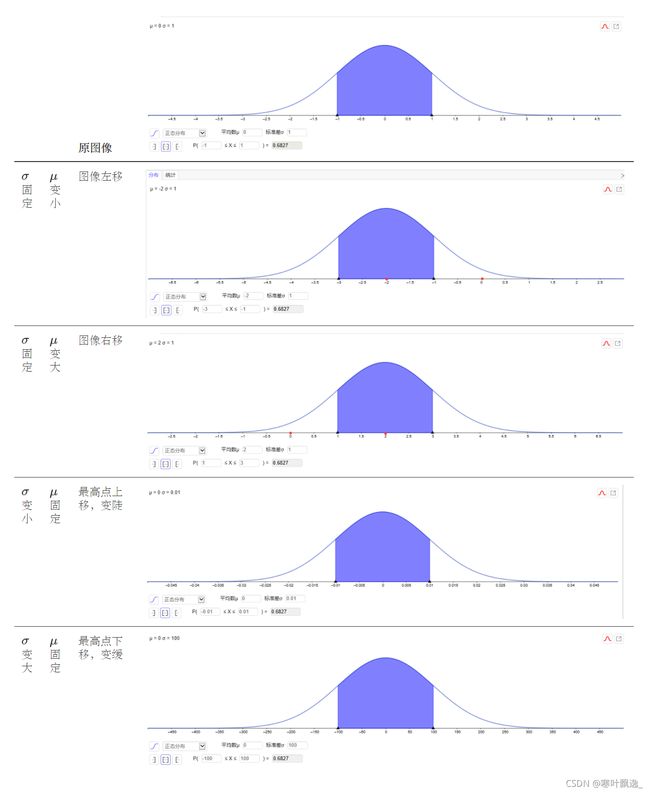
① σ \sigma σ固定, μ \mu μ变化:
图像左右移动,
② μ \mu μ固定, σ \sigma σ变化:
σ \sigma σ变小,最高点上移,变陡; σ \sigma σ变大,最高点下移,变缓
标准正态分布
μ = 0 , σ = 1 \mu=0,\sigma = 1 μ=0,σ=1
ϕ 0 ( x ) = 1 2 π e − x 2 2 , − ∞ < x < + ∞ \phi_0(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}},-\infty
Φ 0 ( x ) = 1 2 π ∫ − ∞ x e − t 2 2 d t \Phi_{0}(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}dt Φ0(x)=2π1∫−∞xe−2t2dt
性质:
y轴为对称轴,偶函数
ϕ 0 ( x ) = ϕ 0 ( − x ) \phi_0(x)=\phi_0(-x) ϕ0(x)=ϕ0(−x)
ϕ 0 ( − x ) = 1 − ϕ 0 ( x ) \phi_0(-x) = 1-\phi_0(x) ϕ0(−x)=1−ϕ0(x)
查表:表只给了 0 ≤ x < 5 0\leq x<5 0≤x<5的值
当 x ≥ 5 x\geq5 x≥5时,认为 ϕ 0 ( x ) = 0 \phi_0(x) = 0 ϕ0(x)=0, Φ 0 ( x ) = 1 \Phi_0(x)=1 Φ0(x)=1
当 x ≤ − 5 x\leq-5 x≤−5时,认为 ϕ 0 ( x ) = 0 \phi_0(x) = 0 ϕ0(x)=0, Φ 0 ( x ) = 1 \Phi_0(x)=1 Φ0(x)=1
当 − 5 < x ≤ 0 -5< x\leq 0 −5<x≤0时,用 Φ 0 ( − x ) = 1 − Φ 0 ( x ) \Phi_0(-x) = 1-\Phi_0(x) Φ0(−x)=1−Φ0(x)来求
一般的正态分布化为标准的正态分布
ϕ ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 \phi(x) = \frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{(x-\mu)^2}{2{\sigma}^2}} ϕ(x)=2πσ1e−2σ2(x−μ)2, − ∞ < x < + ∞ -\infty< x < +\infty −∞<x<+∞
= 1 σ [ 1 2 π e − ( x − μ σ ) 2 2 ] =\frac{1}{\sigma}\big[ \frac{1}{\sqrt{2\pi}}e^{-\frac{(\frac{x-\mu}{\sigma})^2}{2}}\big] =σ1[2π1e−2(σx−μ)2]
= 1 σ ϕ 0 ( x − μ σ ) =\frac{1}{\sigma}\phi_0(\frac{x-\mu}{\sigma}) =σ1ϕ0(σx−μ)
Φ ( x ) = 1 2 π σ ∫ − ∞ x e − ( t − μ ) 2 2 σ 2 d t \Phi(x) = \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{x}e^{-\frac{(t-\mu)^2}{2\sigma ^2}}dt Φ(x)=2πσ1∫−∞xe−2σ2(t−μ)2dt
= 1 2 π ∫ − ∞ x e − ( t − μ σ ) 2 2 d ( x − μ σ ) =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{(\frac{t-\mu}{\sigma})^2}{2}}d(\frac{x-\mu}{\sigma}) =2π1∫−∞xe−2(σt−μ)2d(σx−μ)
= Φ 0 ( x − μ σ ) =\Phi_0(\frac{x-\mu}{\sigma}) =Φ0(σx−μ)
例:
X X X~ N ( 0 , 1 ) N(0,1) N(0,1)
P { ∣ X ∣ ≤ 1.96 } = P { − 1.96 ≤ X ≤ 1.96 } = Φ 0 ( 1.96 ) − Φ 0 ( − 1.96 ) = Φ 0 ( 1.96 ) − ( 1 − Φ 0 ( 1.96 ) ) = 2 × Φ 0 ( 1.96 ) − 1 P\{|X|\leq 1.96\} = P\{-1.96\leq X\leq 1.96\} = \Phi_0(1.96)-\Phi_0(-1.96) \\=\Phi_0(1.96)-(1-\Phi_0(1.96))=2\times \Phi_0(1.96) -1 P{∣X∣≤1.96}=P{−1.96≤X≤1.96}=Φ0(1.96)−Φ0(−1.96)=Φ0(1.96)−(1−Φ0(1.96))=2×Φ0(1.96)−1
例:
X X X~ N ( 1 , 4 ) N(1,4) N(1,4), μ = 1 , σ = 2 \mu=1,\sigma =2 μ=1,σ=2
P { 0 < X < 1.6 } = Φ ( 1.6 ) − Φ ( 0 ) = Φ 0 ( 1.6 − 1 2 ) − Φ 0 ( 0 − 1 2 ) = Φ 0 ( 0.3 ) − Φ 0 ( − 0.5 ) P\{0
例:
生产零件的长度符合正态分布 X X X~ N ( 50 , 1 ) N(50,1) N(50,1),零件长度 50 ± 1 50\pm1 50±1是合格的。
问:①合格的概率
②重复出三次,至少一个合格的概率
① P { 49 ≤ X ≤ 51 } = Φ ( 51 ) − Φ ( 49 ) = Φ 0 ( 51 − 50 1 ) − Φ 0 ( 49 − 50 1 ) = Φ 0 ( 1 ) − Φ 0 ( − 1 ) = 2 Φ 0 ( 1 ) − 1 = 0.6826 P\{49\le X \le 51\} = \Phi(51)-\Phi(49)=\Phi_0(\frac{51-50}{1})-\Phi_0(\frac{49-50}{1})=\\\Phi_0(1)-\Phi_0(-1)=2\Phi_0(1)-1=0.6826 P{49≤X≤51}=Φ(51)−Φ(49)=Φ0(151−50)−Φ0(149−50)=Φ0(1)−Φ0(−1)=2Φ0(1)−1=0.6826
②设Y为合格的个数
P { Y ≥ 1 } = 1 − P { Y = 0 } = 1 − ( 0.6826 ) 3 ≈ 0.968 P\{Y\geq 1\}=1-P\{Y=0\}=1-(0.6826)^3\approx 0.968 P{Y≥1}=1−P{Y=0}=1−(0.6826)3≈0.968
例:
X X X~ N ( μ , σ 2 ) N(\mu,\sigma ^2) N(μ,σ2)
证:① P { ∣ X − μ ∣ < σ } P\{|X-\mu|<\sigma\} P{∣X−μ∣<σ}
② P { ∣ X − μ ∣ < 2 σ } P\{|X-\mu|<2\sigma\} P{∣X−μ∣<2σ}
③ P { ∣ X − μ ∣ < 3 σ } P\{|X-\mu|<3\sigma\} P{∣X−μ∣<3σ}
P { ∣ X − μ ∣ < σ } = P { − σ < X − μ < σ } = P { μ − σ < X < μ + σ } P\{|X-\mu|<\sigma\}=P\{-\sigma
= Φ ( μ + σ ) − Φ ( μ − σ ) =\Phi(\mu+\sigma)-\Phi(\mu-\sigma) =Φ(μ+σ)−Φ(μ−σ)
= Φ 0 ( μ + σ − μ σ ) − Φ 0 ( μ − σ − μ σ ) =\Phi_0(\frac{\mu+\sigma-\mu}{\sigma})-\Phi_0(\frac{\mu-\sigma-\mu}{\sigma}) =Φ0(σμ+σ−μ)−Φ0(σμ−σ−μ)
= Φ 0 ( 1 ) − Φ 0 ( − 1 ) =\Phi_0(1)-\Phi_0(-1) =Φ0(1)−Φ0(−1)
= 2 Φ 0 ( 1 ) − 1 =2\Phi_0(1)-1 =2Φ0(1)−1
= 0.6826 =0.6826 =0.6826
P { ∣ X − μ ∣ < 2 σ } = 0.9544 P\{|X-\mu|<2\sigma\}=0.9544 P{∣X−μ∣<2σ}=0.9544
P { ∣ X − μ ∣ < 3 σ } = 0.9974 P\{|X-\mu|<3\sigma\}=0.9974 P{∣X−μ∣<3σ}=0.9974
3 σ 准 则 3\sigma准则 3σ准则
可以认为,Y 的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%
X X X~ N ( 0 , 1 ) N(0,1) N(0,1),给定 α ( 0 < α < 1 ) \alpha(0<\alpha<1) α(0<α<1),找到一个值 u α u_{\alpha} uα,使得 P { X > u α } = α P\{X>u_{\alpha}\}=\alpha P{X>uα}=α
u α 称 为 上 α 分 位 数 u_{\alpha}称为上\alpha分位数 uα称为上α分位数
2.2.3 0-1分布
| X | 1 | 0 |
|---|---|---|
| P | p | 1-p |
P { x = k } = P k ( 1 − P ) 1 − k , k = 0 , 1 P\{x=k\}=P^k(1-P)^{1-k}, k=0,1 P{x=k}=Pk(1−P)1−k,k=0,1
k = 0 , 1 − p k=0,1-p k=0,1−p
k = 1 , p k=1,p k=1,p
例:
废品率10%, F ( x ) = { 1 合 格 0 废 品 F(x) = \left\{ \begin{array}{rcl} 1 & 合格 \\ 0 & 废品 \end{array}\right. F(x)={10合格废品
P { X = 1 } = 0.9 , P { X = 0 } = 0.1 P\{X=1\}=0.9,P\{X=0\}=0.1 P{X=1}=0.9,P{X=0}=0.1
0-1分布是二项分布的特例
有两种结果,试验只做一次
2.2.3超几何分布
100学生,男60人,女40人,取10人
X:取10人中男生的人数
P { X = k } = C 60 k C 40 10 − k C 100 10 P\{X=k\}=\frac{C_{60}^{k}C_{40}^{10-k}}{C_{100}^{10}} P{X=k}=C10010C60kC4010−k
N个元素分成N_1个属于第一类,N_2个属于第二类
取n个,X:取n个属于第一类的个数
P { X = k } = C N 1 k C N 2 n − k C N n , k = 0 , 1 , . . . , m i n { n , N 1 } P\{X=k\}=\frac{C_{N_1}^{k}C_{N_2}^{n-k}}{C_{N}^{n}},k=0,1,...,min\{n,N_1\} P{X=k}=CNnCN1kCN2n−k,k=0,1,...,min{n,N1}
例:
有20名学生,5女15男,任取4人参加比赛,X:4人中女生的人数
P { X = k } = C 5 k C 15 4 − k C 20 4 , k = 0 , 1 , 2 , 3 , 4 P\{X=k\}=\frac{C_{5}^{k}C_{15}^{4-k}}{C_{20}^{4}},k=0,1,2,3,4 P{X=k}=C204C5kC154−k,k=0,1,2,3,4
不放回抽样试验,N很大,n相对于N很小时, P = M N P=\frac{M}{N} P=NM的改变很小
P { X = k } = C M k C N − M n − k C N n ≈ C n k P k ( 1 − p ) ( n − k ) P\{X=k\}=\frac{C_M^kC_{N-M}^{n-k}}{C_N^n}\approx C_n^kP^k(1-p)^{(n-k)} P{X=k}=CNnCMkCN−Mn−k≈CnkPk(1−p)(n−k)
例:
有10000粒种子,发芽率99%,取200粒,至多1粒不发芽的概率
10000*1% = 100粒 不发芽
9900粒 发芽
N = 10000 , N 1 = 100 , N 2 = 9900 N=10000,N_1=100,N_2=9900 N=10000,N1=100,N2=9900
P { X ≤ 1 } = P { X = 0 } + P { X = 1 } = C 100 0 C 9900 200 C 10000 200 + C 100 1 C 9900 199 C 10000 200 P\{X\leq1\}=P\{X=0\}+P\{X=1\}=\frac{C_{100}^{0}C_{9900}^{200}}{C_{10000}^{200}}+\frac{C_{100}^{1}C_{9900}^{199}}{C_{10000}^{200}} P{X≤1}=P{X=0}+P{X=1}=C10000200C1000C9900200+C10000200C1001C9900199
≈ C 200 0 0.0 1 0 ( 1 − 0.01 ) 200 + C 200 1 0.0 1 1 ( 1 − 0.01 ) 199 \approx C_{200}^{0}0.01^0(1-0.01)^{200}+C_{200}^{1}0.01^1(1-0.01)^{199} ≈C20000.010(1−0.01)200+C20010.011(1−0.01)199
≈ 0.406 \approx 0.406 ≈0.406
二项分布, n ≥ 100 , n p ≤ 10 n\geq100,np\leq10 n≥100,np≤10时,用泊松分布近似计算 λ = n p \lambda = np λ=np
超 几 何 分 布 ⟶ 二 项 分 布 ⟶ 泊 松 分 布 超几何分布\longrightarrow 二项分布 \longrightarrow 泊松分布 超几何分布⟶二项分布⟶泊松分布
2.2.3二项分布
P ( A ) = O , 做 了 n 次 试 验 , 发 生 了 k 次 P(A)=O,做了n次试验,发生了k次 P(A)=O,做了n次试验,发生了k次
P { X = K } = C N k P k ( 1 − P ) n − k , k = 0 , 1 , 2 … , n P\{X=K\}=C_N^k P^k(1-P)^{n-k},k=0,1,2…,n P{X=K}=CNkPk(1−P)n−k,k=0,1,2…,n
X X X~ B ( n , p ) B(n,p) B(n,p)
最可能值:
-
(n+1)p不为整数,[(n+1)p]达最大值
-
(n+1)p是整数,(n+1)p、()
例:
报警器,每台报警的机率是0.8,以99%的机率报警需要多少台报警器
X : X: X:发生危险时报警的台数
n : n: n:安装的台数
P { x ≥ 1 } = 1 − P { X = 0 } = 1 − C n 0 0. 2 n P\{x\geq 1\}=1-P\{X=0\}=1-C_n^00.2^n P{x≥1}=1−P{X=0}=1−Cn00.2n
1 − 0. 2 n ≥ 0.99 1-0.2^n\geq 0.99 1−0.2n≥0.99
0.01 ≥ 0. 2 n 0.01\geq 0.2^n 0.01≥0.2n
ln 0.01 ≥ n ln 0.2 \ln 0.01\geq n\ln0.2 ln0.01≥nln0.2
n ≥ ln 0.01 ln 0.2 n\geq \frac{\ln0.01}{\ln0.2} n≥ln0.2ln0.01
n ≥ 3 n\geq 3 n≥3
例:
每台机床需要维修的概率P=0.01
1.1个人看管20台
X:为需要维修的台数
P { X > 1 } = 1 − P { X = 0 } − P { X = 1 } P\{X>1\}=1-P\{X=0\}-P\{X=1\} P{X>1}=1−P{X=0}−P{X=1}
= 1 − C 2 0 0 0.9 9 2 0 − C 2 0 1 0.01 × 0.9 9 1 9 =1-C_20^00.99^20-C_20^10.01\times 0.99^19 =1−C2000.9920−C2010.01×0.9919
≈ 0.0169 \approx0.0169 ≈0.0169
- 3个人看管80台
P { X > 3 } = 1 − P { X = 0 } − P { X = 1 } − P { X = 2 } − P { X = 3 } ≈ 0.0087 P\{X>3\}=1-P\{X=0\}-P\{X=1\}-P\{X=2\}-P\{X=3\}\approx0.0087 P{X>3}=1−P{X=0}−P{X=1}−P{X=2}−P{X=3}≈0.0087
2.2.3几何分布
P ( A ) = P , 第 k 次 首 次 发 生 , 前 k − 1 次 未 发 生 P(A)=P,第k次首次发生,前k-1次未发生 P(A)=P,第k次首次发生,前k−1次未发生
P { X = k } = ( 1 − p ) k − 1 p P\{X=k\}=(1-p)^{k-1}p P{X=k}=(1−p)k−1p X X X ~ G ( p ) G(p) G(p)
例:
射中概率0.6,X:直到命中目标的次数
P { X = k } = 0. 4 k − 1 0.6 P\{X=k\}=0.4^{k-1}0.6 P{X=k}=0.4k−10.6, k = 1 , 2 , 3 , . . . k=1,2,3,... k=1,2,3,...
连续型的分布
2.2.3均匀分布
f ( x ) = { 1 b − a a ≤ x ≤ b 0 其 他 f(x) = \left\{ \begin{array}{rcl} \frac{1}{b-a} & a\leq x \leq b \\ 0 & 其他 \end{array}\right. f(x)={b−a10a≤x≤b其他
x ∼ U [ a , b ] x\sim U[a,b] x∼U[a,b]
分布函数
F ( x ) = ∫ − ∞ x f ( t ) d t F(x) = \int_{-\infty}^{x}f(t)dt F(x)=∫−∞xf(t)dt
F ( x ) = { 0 x < a x − a b − a a ≤ x < b 1 x ≥ b F(x) = \left\{ \begin{array}{rcl} 0 & xF(x)=⎩⎨⎧0b−ax−a1x<aa≤x<bx≥b
X ∼ U [ a , b ] X\sim U[a,b] X∼U[a,b], [ c , d ] ⊂ [ a , b ] [c,d]\sub [a,b] [c,d]⊂[a,b]
P { c ≤ x ≤ d } = ∫ c d 1 b − a d t = d − c b − a P\{c\leq x\leq d\} = \int_{c}^{d}\frac{1}{b-a}dt = \frac{d-c}{b-a} P{c≤x≤d}=∫cdb−a1dt=b−ad−c
例:公共汽车从7点开始每15分钟开一班车,乘客从7点到7点半到达车站是一个均匀分布
问: ①等车不超过五分钟的概率
②等车超过十分钟的概率
过X分钟到达车站,X~U[0,30]
f ( x ) = { 1 30 0 ≤ x ≤ 30 0 其 他 f(x) = \left\{ \begin{array}{rcl} \frac{1}{30} & 0\leq x \leq 30 \\ 0 & 其他 \end{array}\right. f(x)={30100≤x≤30其他
① P { 10 ≤ x ≤ 15 } + P { 25 ≤ x ≤ 30 } = 5 30 + 5 30 = 1 3 P\{10\leq x\leq 15\}+P\{25\leq x\leq 30\}=\frac{5}{30}+\frac{5}{30}=\frac{1}{3} P{10≤x≤15}+P{25≤x≤30}=305+305=31
② P { 0 ≤ x < 5 } + P { 15 < x < 20 } = 1 3 P\{0\leq x<5\}+P\{15< x< 20\}=\frac{1}{3} P{0≤x<5}+P{15<x<20}=31
2.2.3泊松分布
P { X = k } = λ k k ! e − λ , k = 0 , 1 , 2 , . . . , λ > 0 P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda},k=0,1,2,...,\lambda>0 P{X=k}=k!λke−λ,k=0,1,2,...,λ>0
X ∼ P ( λ ) X\sim P(\lambda) X∼P(λ)
电话台呼叫次数,公用设施(等车,收银台)
二项分布:
0.99^20可以用泊松分布来近似
n较大p较小,np适中
n ≥ 100 , n p ≤ 10 n\geq100,np\leq10 n≥100,np≤10
例:
电话台,每分钟的用户呼叫次数X~P(3) λ = 3 \lambda=3 λ=3
一分钟内呼叫不超过5次的概率
X X X~ P ( 3 ) , λ = 3 P(3),\lambda=3 P(3),λ=3
P { X = k } = λ k k ! e − λ = 3 k k ! e − 3 , k = 0 , 1 , 2 , . . . P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda}=\frac{3^k}{k!}e^{-3},k=0,1,2,... P{X=k}=k!λke−λ=k!3ke−3,k=0,1,2,...
P { X ≤ 5 } = ∑ k = 0 5 P { X = k } = 0.916 P\{X\leq5\}=\sum_{k=0}^{5}P\{X=k\}=0.916 P{X≤5}=∑k=05P{X=k}=0.916
例:
证券部有1000个账户,每户10万元,每户提20%的概率是0.006,问:需要准备多少现金才能以95%以上的概率保证用户提款的要求
10 × 0.2 = 2 10\times0.2=2 10×0.2=2万元
n = 1000 n=1000 n=1000, p = 0.006 p=0.006 p=0.006, n p = 6 np=6 np=6, λ = 6 \lambda=6 λ=6
X:表示来提钱的用户数,X~B(1000,0.006)
现金x元
P { 2 X ≤ x } ≥ 0.95 P\{2X\leq x\}\geq 0.95 P{2X≤x}≥0.95
P { X ≤ x 2 } ≥ 0.95 P\{X\leq \frac{x}{2}\}\geq 0.95 P{X≤2x}≥0.95
∑ k = 0 x 2 6 k k ! e − 6 ≥ 0.95 \sum_{k=0}^{\frac{x}{2}}\frac{6^k}{k!}e^{-6}\geq0.95 ∑k=02xk!6ke−6≥0.95
x 2 ≥ 10 \frac{x}{2}\geq 10 2x≥10
x ≥ 20 x\geq20 x≥20
上面的式子需要查表计算,先找到 λ = 6 \lambda=6 λ=6,然后把k=0,1,…的值一直加,直到它的值大于等于0.95
在k=10的时候,超过0.95
例:
某种非传染病,发病率=0.001,有一单位有5000人,问至少两人得病的概率
X:得病的人数,X~B(5000,0.001)
n=5000,np=5, λ = 5 \lambda=5 λ=5
P { X ≥ 2 } = 1 − P { X = 0 } − P { X = 1 } P\{X\geq 2\}=1-P\{X=0\}-P\{X=1\} P{X≥2}=1−P{X=0}−P{X=1}
= 1 − 0.006738 − 0.03369 =1-0.006738-0.03369 =1−0.006738−0.03369
= 0.959572 =0.959572 =0.959572
2.2.3指数分布
f ( x ) = { λ e − λ x x > 0 0 x ≤ 0 f(x) = \left\{ \begin{array}{rcl} \lambda e^{-\lambda x} & x > 0 \\ 0 & x\leq 0 \end{array}\right. f(x)={λe−λx0x>0x≤0
λ > 0 \lambda >0 λ>0, x x x~ e x p ( λ ) exp(\lambda) exp(λ)
F ( x ) = { 1 − e − λ x x > 0 0 x ≤ 0 F(x) = \left\{ \begin{array}{rcl} \ 1-e^{-\lambda x}& x > 0 \\ 0 & x\leq 0 \end{array}\right. F(x)={ 1−e−λx0x>0x≤0
F ( x ) = P { X ≤ x } F(x) = P\{X\leq x\} F(x)=P{X≤x}
= ∫ − ∞ x f ( t ) d t =\int_{- \infty }^xf(t)dt =∫−∞xf(t)dt
1 − e − λ x 1-e^{-\lambda x} 1−e−λx
例:机器的寿命X为
f ( x ) = { 1 1000 e − x 1000 x > 0 0 x ≤ 0 f(x) = \left\{ \begin{array}{rcl} \frac{1}{1000}e^{-\frac{x}{1000}} & x>0 \\ 0 & x\leq 0 \end{array}\right. f(x)={10001e−1000x0x>0x≤0
机器有3个元件,求这个机器工作1000小时以上的概率
P { X > 1000 } = ∫ 1000 + ∞ e − x 1000 d x = − e − x 1000 ∣ 1000 + ∞ = e − 1 P\{X>1000\} = \int_{1000}^{+\infty}e^{-\frac{x}{1000}}dx = -e^{-\frac{x}{1000}}|_{1000}^{+\infty} = e^{-1} P{X>1000}=∫1000+∞e−1000xdx=−e−1000x∣1000+∞=e−1
P ( A ) = ( P ( x > 1000 ) ) 3 = e − 3 P(A) = (P(x>1000))^3 = e^{-3} P(A)=(P(x>1000))3=e−3
例:
X是指数分布,参数为 λ \lambda λ,s>0,t>0,证 P { X > s + t ∣ x > s } = P { X > t } P\{X>s+t|x>s\}=P\{X>t\} P{X>s+t∣x>s}=P{X>t}
指数分布具有无记忆性
P { X > s + t ∣ X > t } = P { { X > s + t } ⋂ { X > s } } P { X > s } = P { X > s + t } P { X > s } = ∫ s + t + ∞ λ e − λ x d x ∫ s + ∞ λ e − λ x d x = − e − λ x ∣ s + t + ∞ − e − λ x ∣ s + ∞ = e − λ ( s + t ) e − λ ( s ) = e − λ t P\{X>s+t|X>t\} = \frac{P\big\{\{X>s+t\}\bigcap\{X>s\}\big\}}{P\{X>s\}} = \frac{P\{X>s+t\}}{P\{X>s\}} = \frac{\int_{s+t}^{+\infty}\lambda e^{-\lambda x}dx}{\int_{s}^{+\infty}\lambda e^{-\lambda x}dx} = \frac{-e^{-\lambda x}|_{s+t}^{+\infty}}{-e^{-\lambda x}|_{s}^{+\infty}} = \frac{e^{-\lambda (s+t)}}{e^{-\lambda (s)}} = e^{-\lambda t} P{X>s+t∣X>t}=P{X>s}P{{X>s+t}⋂{X>s}}=P{X>s}P{X>s+t}=∫s+∞λe−λxdx∫s+t+∞λe−λxdx=−e−λx∣s+∞−e−λx∣s+t+∞=e−λ(s)e−λ(s+t)=e−λt
P { X > t } = ∫ t + ∞ λ e − λ x d x = − e − λ x ∣ t + ∞ = e − λ t P\{X>t\} = \int_{t}^{+\infty}\lambda e^{-\lambda x}dx = -e^{-\lambda x}|^{+\infty}_{t} = e^{-\lambda t} P{X>t}=∫t+∞λe−λxdx=−e−λx∣t+∞=e−λt
2.3.1 随机变量函数的分布(离散型)
已知X是某分布, Y = 3 X − 5 Y=3X-5 Y=3X−5,问Y的分布函数是什么
例:
-
X是离散型的变量
X 7 8 9 10 P 0.1 0.3 0.4 0.2 Y = 4 X Y=4X Y=4X
| Y | 28 | 32 | 36 | 40 |
|---|---|---|---|---|
| P | 0.1 | 0.3 | 0.4 | 0.2 |
Z = X 2 Z=X^2 Z=X2
| Z | 49 | 64 | 81 | 100 |
|---|---|---|---|---|
| P | 0.1 | 0.3 | 0.4 | 0.2 |
| X | -1 | 0 | 1 | 2 |
|---|---|---|---|---|
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Y = X 2 Y=X^2 Y=X2
| X | 1 | 0 | 1 | 4 |
|---|---|---|---|---|
| P | 0.2 | 0.3 | 0.4 | 0.1 |
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
| X | 0 | 1 | 4 |
|---|---|---|---|
| P | 0.3 | 0.6 | 0.1 |
2.3.2 随机变量函数的分布(连续型)
连续型
分布函数 F ( x ) = P { X ≤ x } F(x)=P\{X\leq x\} F(x)=P{X≤x}
F X ( x ) = P { X ≤ x } F_X(x)=P\{X\leq x\} FX(x)=P{X≤x}
F Y ( x ) = P { Y ≤ x } F_Y(x) = P\{Y\leq x\} FY(x)=P{Y≤x}
假设 X X X的密度函数是 f X ( x ) , y = g ( x ) , Y = g ( X ) , f_X(x),y=g(x),Y=g(X), fX(x),y=g(x),Y=g(X),求Y的密度函数
① F Y ( x ) ⟶ F X ( x ) F_Y(x)\longrightarrow F_X(x) FY(x)⟶FX(x) 两边求导
② f Y ( x ) ⟵ f X ( x ) f_Y(x)\longleftarrow f_X(x) fY(x)⟵fX(x)
例:
X的密度函数为 f X ( x ) , Y = 3 X + 2 f_X(x),Y=3X+2 fX(x),Y=3X+2
解:
F Y ( x ) = P { Y ≤ x } = P { 3 X + 2 ≤ x } = P { X ≤ x − 2 3 } = F X ( x − 2 3 ) F_Y(x)=P\{Y\leq x\}=P\{3X+2\leq x\}=P\{X\leq \frac{x-2}{3}\}=F_X(\frac{x-2}{3}) FY(x)=P{Y≤x}=P{3X+2≤x}=P{X≤3x−2}=FX(3x−2)
即 F Y ( x ) = F X ( x − 2 3 ) F_Y(x)=F_X(\frac{x-2}{3}) FY(x)=FX(3x−2) 两边同时求导可得
f Y ( x ) = 1 3 f x ( x − 2 3 ) f_Y(x)=\frac{1}{3}f_x(\frac{x-2}{3}) fY(x)=31fx(3x−2)
特别地,若 f X ( x ) = { 1 4 0 ≤ x ≤ 4 0 e l s e f_X(x) = \left\{ \begin{array}{rcl} \frac{1}{4} & 0\leq x \leq 4 \\ 0 & else \end{array}\right. fX(x)={4100≤x≤4else
则 f Y ( x ) = { 1 12 2 ≤ x ≤ 14 0 e l s e f_Y(x) = \left\{ \begin{array}{rcl} \frac{1}{12} & 2\leq x \leq 14 \\ 0 & else \end{array}\right. fY(x)={12102≤x≤14else
若 X X X服从 [ a , b ] [a,b] [a,b]的均匀分布, Y = k X + C ( k ≠ 0 ) Y=kX+C(k\neq0) Y=kX+C(k=0)服从相应区间上的均匀分布
k > 0 k>0 k>0 f Y ( x ) = { 1 k b − k a k a + c ≤ x ≤ k b + c 0 e l s e f_Y(x) = \left\{ \begin{array}{rcl} \frac{1}{kb-ka} & ka+c\leq x \leq kb+c \\ 0 & else \end{array}\right. fY(x)={kb−ka10ka+c≤x≤kb+celse
k < 0 k<0 k<0 f Y ( x ) = { 1 k a − k b k b + c ≤ x ≤ k a + c 0 e l s e f_Y(x) = \left\{ \begin{array}{rcl} \frac{1}{ka-kb} & kb+c\leq x \leq ka+c \\ 0 & else \end{array}\right. fY(x)={ka−kb10kb+c≤x≤ka+celse
例:假设 X X X~ N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2), Y = a X + b Y=aX+b Y=aX+b, a ≠ 0 a\neq 0 a=0
解:
a > 0 a>0 a>0时
F Y ( x ) = P { Y ≤ x } = P { a X + b ≤ x } = P { x ≤ x − b a } = Φ ( x − b a ) F_Y(x)=P\{Y\leq x\}=P\{aX+b\leq x\}=P\{x\leq\frac{x-b}{a}\}=\Phi(\frac{x-b}{a}) FY(x)=P{Y≤x}=P{aX+b≤x}=P{x≤ax−b}=Φ(ax−b)
f Y ( x ) = 1 a ϕ ( x − b a ) = 1 2 π σ e − ( x − b a − μ ) 2 2 σ 2 1 a f_Y(x)=\frac{1}{a}\phi(\frac{x-b}{a})=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\frac{x-b}{a}-\mu)^2}{2\sigma^2}}\frac{1}{a} fY(x)=a1ϕ(ax−b)=2πσ1e−2σ2(ax−b−μ)2a1
= 1 2 π a σ e − ( x − ( b + a μ ) ) 2 2 a 2 σ 2 =\frac{1}{\sqrt{2\pi}a\sigma}e^{-\frac{(x-(b+a\mu))^2}{2a^2\sigma^2}} =2πaσ1e−2a2σ2(x−(b+aμ))2 一般的正态分布的密度函数: φ ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 \varphi(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} φ(x)=2πσ1e−2σ2(x−μ)2
所以 X X X~ N ( a μ + b , a 2 σ 2 ) N(a\mu+b,a^2\sigma^2) N(aμ+b,a2σ2)
a < 0 a<0 a<0时
f Y ( x ) = 1 2 π ( − a σ ) e − ( x − ( b + a μ ) ) 2 2 a 2 σ 2 f_Y(x)=\frac{1}{\sqrt{2\pi}(-a\sigma)}e^{-\frac{(x-(b+a\mu))^2}{2a^2\sigma^2}} fY(x)=2π(−aσ)1e−2a2σ2(x−(b+aμ))2
综上, f Y ( x ) = 1 2 π ∣ a ∣ σ e − ( x − ( b + a μ ) ) 2 2 a 2 σ 2 f_Y(x)=\frac{1}{\sqrt{2\pi}|a|\sigma}e^{-\frac{(x-(b+a\mu))^2}{2a^2\sigma^2}} fY(x)=2π∣a∣σ1e−2a2σ2(x−(b+aμ))2
在这题里 Y = a X + b Y=aX+b Y=aX+b是线性函数,所以他还是服从正态分布
若 Y = X − μ σ Y=\frac{X-\mu}{\sigma} Y=σX−μ, N ( 0 , 1 ) N(0,1) N(0,1)
定理1: X X X的密度函数为 f X ( x ) f_X(x) fX(x),则引入 Y = k X + b , k ≠ 0 Y=kX+b,k\neq0 Y=kX+b,k=0,密度函数是 f Y ( x ) = 1 ∣ k ∣ f x ( x − b k ) f_Y(x)=\frac{1}{|k|}f_x(\frac{x-b}{k}) fY(x)=∣k∣1fx(kx−b)
证:k<0时, F Y ( x ) = P { Y ≤ x } = P { k X + b ≤ x } = P { X ≥ x − b k } = 1 − P { X ≤ x − b k } F_Y(x)=P\{Y\leq x\}=P\{kX+b \leq x\}=P\{X\geq \frac{x-b}{k}\}=1-P\{X\leq \frac{x-b}{k}\} FY(x)=P{Y≤x}=P{kX+b≤x}=P{X≥kx−b}=1−P{X≤kx−b}因为这里是连续型的,所以可以取等号
= 1 − F x ( x − b k ) =1-F_x(\frac{x-b}{k}) =1−Fx(kx−b)
f Y ( x ) = − 1 k f x ( x − b k ) f_Y(x)=-\frac{1}{k}f_x(\frac{x-b}{k}) fY(x)=−k1fx(kx−b)
k>0时, f Y ( x ) = 1 k f x ( x − b k ) f_Y(x)=\frac{1}{k}f_x(\frac{x-b}{k}) fY(x)=k1fx(kx−b)
综上, f Y ( x ) = 1 ∣ k ∣ f x ( x − b k ) f_Y(x)=\frac{1}{|k|}f_x(\frac{x-b}{k}) fY<