《深度学习入门》第5期-从感知机到神经网络-码农解书(视频)
前两期的节目介绍了感知机的内容,本期节目将开始解读《深度学习入门》这本书的第3章神经网络的内容,将从感知机迈入神经网络的世界,重点介绍感知机与神经网络的区别。
这里需要说明的是,这本书中,在使用“感知机”一词时,没有严格统一它所指的算法。一般而言,“朴素感知机”是指单层网络,指的是激活函数使用了阶跃函数(后述)的模型。“多层感知机”是指神经网络,即使用sigmoid函数(后述)等平滑的激活函数的多层网络。
感知机与神经网络有很多共同点,为了引出对神经网络的介绍,这里主要介绍二者的区别。首先给出结论,然后再给出解释说明。
感知机与神经网络的区别
1. 从构建的角度来看:二者确定参数的方式不同
- 对于感知机而言,设定参数的工作,即确定合适的、能符合预期的输入与输出的参数,是由人工进行的;
- 对于神经网络而言,自动地从数据中学习到合适的参数。
在这本书第2章感知机的介绍中,我们结合与门、与非门、或门的真值表人工决定了合适的参数。关于神经网络如何自动学习合适的参数,将会在后面的章节中介绍。
2. 从实现的角度来看:二者所使用的激活函数不同:
- 感知机中使用了阶跃函数作为激活函数;
- 神经网络中使用了sigmoid函数、ReLU函数等作为激活函数。
下面我们就来看一下什么是激活函数。
激活函数
首先从感知机的激活函数说起。
1. 感知机公式第1版:
我们先来回顾一下感知机的公式表示:
y = { 0 , ( b + w 1 x 1 + w 2 x 2 ≤ 0 ) 1 , ( b + w 1 x 1 + w 2 x 2 > 0 ) y = \begin{cases} 0, & (b + w_1 x_1 +w_2 x_2 \leq 0)\\ 1, & (b + w_1 x_1 +w_2 x_2 > 0) \end{cases} y={0,1,(b+w1x1+w2x2≤0)(b+w1x1+w2x2>0)
2. 感知机公式第2版:
我们引入一个新的函数 h ( x ) h(x) h(x),那么感知机就可以表示为如下形式:
y = h ( b + w 1 x 1 + w 2 x 2 ) y = h(b + w_1 x_1 +w_2 x_2) y=h(b+w1x1+w2x2)
h ( x ) = { 0 , ( x ≤ 0 ) 1 , ( x > 0 ) h(x) = \begin{cases} 0, & (x \leq 0)\\ 1, & (x > 0) \end{cases} h(x)={0,1,(x≤0)(x>0)
3. 激活函数登场:
刚刚登场的这个函数 h ( x ) h(x) h(x)就是激活函数,它所起到的作用是,将输入信号的总和转化为输出信号。为了能更清楚地表示激活函数的作用,我们对其进行进一步地改写:
a = b + w 1 x 1 + w 2 ∗ x 2 a = b + w_1 x_1 + w_2 * x_2\\ a=b+w1x1+w2∗x2
y = h ( a ) y = h(a) y=h(a)
这样修改以后, a a a就表示加权输入信号和偏置的总和,然后用 h ( ) h() h()函数将 a a a转化为输出 y y y。
我们可以使用图形来明确地显示激活函数的计算过程:

最右侧表示神经元的 ◯ \bigcirc ◯中明确显示了激活函数的计算过程,即信号的加权总和为节点 a a a,然后节点 a a a被激活函数 h ( ) h() h()转换成节点 y y y。
至此,激活函数已经闪亮登场。激活函数是连接感知机和神经网络的桥梁。我们再来回顾一下前面提到的内容:感知机的激活函数是阶跃函数,神经网络的激活函数是sigmoid、ReLU的函数,下面我们就来依次看一下这几个函数的情况。
常用的激活函数
1. 阶跃函数(感知机)
-
公式:
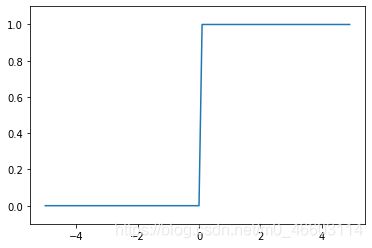
h ( x ) = { 0 , ( x ≤ 0 ) 1 , ( x > 0 ) h(x) = \begin{cases} 0, & (x \leq 0)\\ 1, & (x > 0) \end{cases} h(x)={0,1,(x≤0)(x>0) -
说明
阶跃函数以0为界,输出从0切换为1(或者从1切换为0)。它的值呈阶梯式变化,所以称为阶跃函数。
2. sigmoid函数(神经网络)
-
公式:
h ( x ) = 1 1 + e x p ( − x ) h(x) = \frac{1}{1 + exp(-x)} h(x)=1+exp(−x)1 -
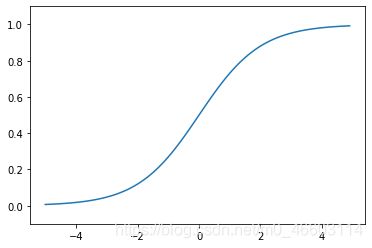
图形:
- 说明:
与阶跃函数对比,sigmoid函数的“平滑性”不同。sigmoid 函数是一条平滑的曲线,输出随着输入发生连续性的变化。而阶跃函数以0为界,输出发生急剧性的变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。
另一个不同点是,相对于阶跃函数只能返回0或1,sigmoid函数可以返回0.731 . . .、0.880 . . .等实数(这一点和刚才的平滑性有关)。也就是说,感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续的实数值信号。
3. ReLU函数(神经网络)
- 公式:
h ( x ) = { x , ( x > 0 ) 0 , ( x ≤ 0 ) h(x) = \begin{cases} x, & (x > 0)\\ 0, & (x \leq 0) \end{cases} h(x)={x,0,(x>0)(x≤0)
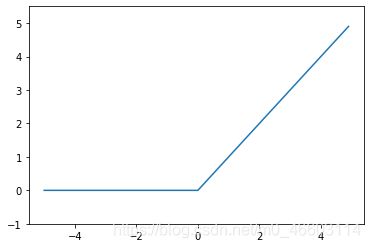
- 图形:
- 说明:
ReLU 函数在输入大于 0 时,直接输出该值;在输入小于等于 0 时,输出0。
小结
在感知机中,我们实际上已经使用了激活函数(阶跃函数),当我们使用新的激活函数(sigmoid、ReLU函数)后,就由感知机进入了神经网络的世界。
更多内容请参见第5期视频:
《深度学习入门》第5期-从感知机到神经网络-码农解书
欢迎大家留言关注,多提意见,谢谢!