神经网络与深度学习作业8:RNN - 简单循环网络
神经网络与深度学习作业8:RNN - 简单循环网络
- 1. 使用Numpy实现SRN
- 2. 在1的基础上,增加激活函数tanh
- 3. 分别使用nn.RNNCell、nn.RNN实现SRN
- 4. 分析“二进制加法” 源代码(选做)
- 5. 实现“Character-Level Language Models”源代码(必做)
- 6. 分析“序列到序列”源代码(选做)
- 7. “编码器-解码器”的简单实现(必做)
- 总结
- References:
简单循环网络 ( Simple Recurrent Network , SRN) 只有一个隐藏层的神经网络 .
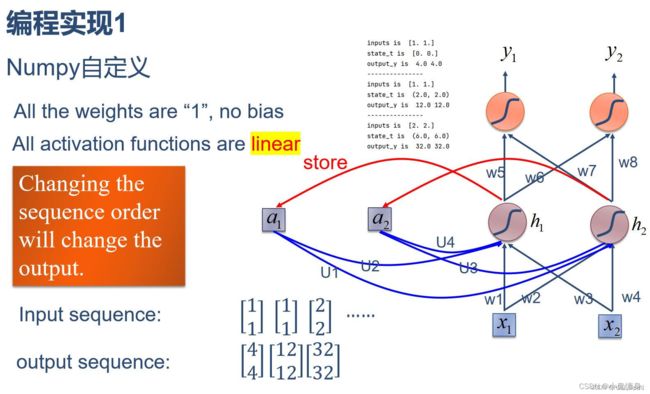
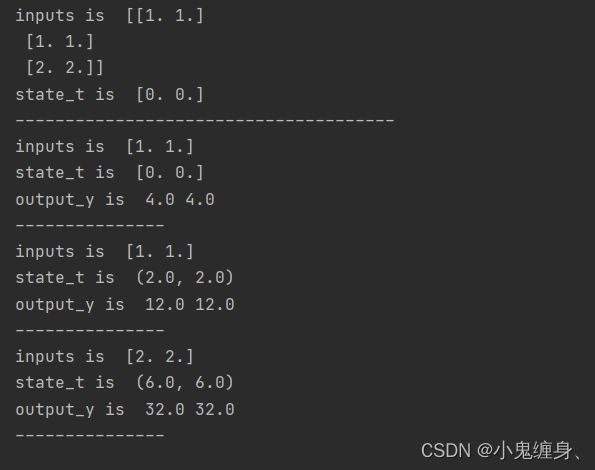
1. 使用Numpy实现SRN
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
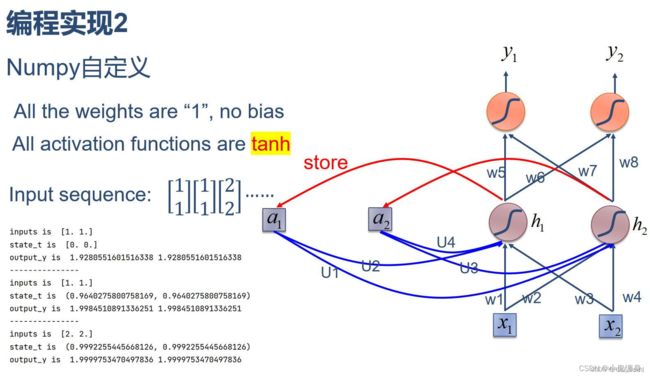
2. 在1的基础上,增加激活函数tanh
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
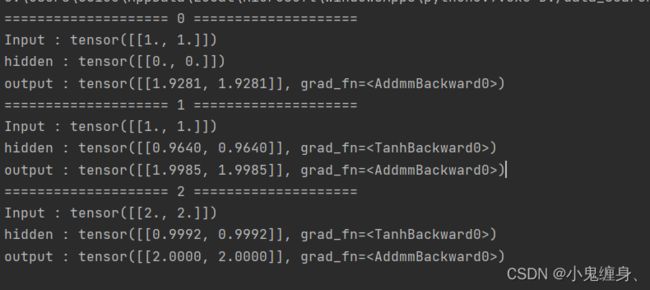
3. 分别使用nn.RNNCell、nn.RNN实现SRN
使用nn.RNNCell实现SRN:
import torch
batch_size = 1
seq_len = 3 # 序列长度
input_size = 2 # 输入序列维度
hidden_size = 2 # 隐藏层维度
output_size = 2 # 输出层维度
# RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# 初始化参数 https://zhuanlan.zhihu.com/p/342012463
for name, param in cell.named_parameters():
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
seq = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(batch_size, hidden_size)
output = torch.zeros(batch_size, output_size)
for idx, input in enumerate(seq):
print('=' * 20, idx, '=' * 20)
print('Input :', input)
print('hidden :', hidden)
hidden = cell(input, hidden)
output = liner(hidden)
print('output :', output)
import torch
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
for name, param in cell.named_parameters(): # 初始化参数
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
inputs = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))
4. 分析“二进制加法” 源代码(选做)
import copy, numpy as np
np.random.seed(0)
#定义sigmoid函数
def sigmoid(x):
output = 1 / (1 + np.exp(-x))
return output
#定义sigmoid导数
def sigmoid_output_to_derivative(output):
return output * (1 - output)
#训练数据的产生
int2binary = {}
binary_dim = 8 #定义二进制位的长度
largest_number = pow(2, binary_dim)#定义数据的最大值
binary = np.unpackbits(
np.array([range(largest_number)], dtype=np.uint8).T, axis=1)#函数产生包装所有符合的二进制序列
for i in range(largest_number):#遍历从0-256的值
int2binary[i] = binary[i]#对于每个整型值赋值二进制序列
print(int2binary)
# 产生输入变量
alpha = 0.1 #设置更新速度(学习率)
input_dim = 2 #输入维度大小
hidden_dim = 16 #隐藏层维度大小
output_dim = 1 #输出维度大小
# 随机产生网络权重
synapse_0 = 2 * np.random.random((input_dim, hidden_dim)) - 1
synapse_1 = 2 * np.random.random((hidden_dim, output_dim)) - 1
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1
#梯度初始值设置为0
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)
#训练逻辑
for j in range(10000):
# 产生一个简单的加法问题
a_int = np.random.randint(largest_number / 2) # 产生一个加法操作数
a = int2binary[a_int] # 找到二进制序列编码
b_int = np.random.randint(largest_number / 2) # 产生另一个加法操作数
b = int2binary[b_int] # 找到二进制序列编码
# 计算正确值(标签值)
c_int = a_int + b_int
c = int2binary[c_int] # 得到正确的结果序列
# 设置存储器,存储中间值(记忆功能)
d = np.zeros_like(c)
overallError = 0 #设置误差
layer_2_deltas = list()
layer_1_values = list()
layer_1_values.append(np.zeros(hidden_dim))
# moving along the positions in the binary encoding
for position in range(binary_dim):
# 产生输入和输出
X = np.array([[a[binary_dim - position - 1], b[binary_dim - position - 1]]])
y = np.array([[c[binary_dim - position - 1]]]).T
# 隐藏层计算
layer_1 = sigmoid(np.dot(X, synapse_0) + np.dot(layer_1_values[-1], synapse_h))
# 输出层
layer_2 = sigmoid(np.dot(layer_1, synapse_1))
# 计算差别
layer_2_error = y - layer_2
#计算每个梯度
layer_2_deltas.append((layer_2_error) * sigmoid_output_to_derivative(layer_2))
#计算所有损失
overallError += np.abs(layer_2_error[0])
# 编码记忆的中间值
d[binary_dim - position - 1] = np.round(layer_2[0][0])
# 拷贝副本
layer_1_values.append(copy.deepcopy(layer_1))
future_layer_1_delta = np.zeros(hidden_dim)
for position in range(binary_dim):
X = np.array([[a[position], b[position]]])
layer_1 = layer_1_values[-position - 1]
prev_layer_1 = layer_1_values[-position - 2]
# 输出层误差
layer_2_delta = layer_2_deltas[-position - 1]
# 隐藏层误差
layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(
synapse_1.T)) * sigmoid_output_to_derivative(layer_1)
# 计算梯度
synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
synapse_0_update += X.T.dot(layer_1_delta)
future_layer_1_delta = layer_1_delta
#梯度下降
synapse_0 += synapse_0_update * alpha
synapse_1 += synapse_1_update * alpha
synapse_h += synapse_h_update * alpha
#重新初始化
synapse_0_update *= 0
synapse_1_update *= 0
synapse_h_update *= 0
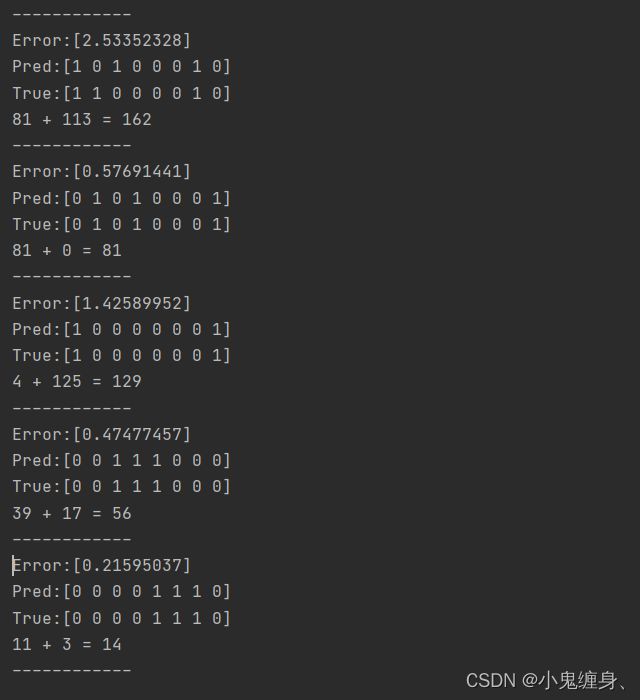
# 打印训练过程
if (j % 1000 == 0):
print("Error:" + str(overallError))
print("Pred:" + str(d))
print("True:" + str(c))
out = 0
for index, x in enumerate(reversed(d)):
out += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out))
print("------------")
分析:
代码注释已经写出,不会理解的自行理解,对于实现的过程把握如下:

- 先定义sigmoid和sigmoid导数函数,方便后序运算
- 初始化8位二进制序列的编码,0-256分别对应00000000-11111111的编码序列。
- 随机产生网络权重,设置随机种子保证每次产生的权重相同,d是存储器,即具有记忆功能的代码
- 每次训练我们在0-128中随机产生两个数(不是0-256防止溢出),找到对应的8位二进制序列,进行数据输入。
- 开始训练,每1000次查看一次中间结果,产生的结果和正确的结果进行误差计算,从而更新随机网络权重的参数,再次训练再更新,直至我们训练10000次为止(或者可以设置误差小于多少停止)。
5. 实现“Character-Level Language Models”源代码(必做)
import numpy as np
import random
#utils.py中定义了本次实验所需要的辅助函数
#包括朴素RNN的前向/反向传播 和我们在上一个实验中实现的差不多
from utils import *
data = open('D:/dinos.txt', 'r').read() #读取dinos.txt中的所有恐龙名字 read()逐字符读取 返回一个字符串
data= data.lower()#把所有名字转为小写
chars = list(set(data))#得到字符列表并去重
print(chars) #'a'-'z' '\n' 27个字符
data_size, vocab_size = len(data), len(chars)
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))
char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }
ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }
print(ix_to_char)
def softmax(x):
''''softmax激活函数'''
e_x = np.exp(x - np.max(x)) # 首先对输入做一个平移 减去最大值 使其最大值为0 再取exp 避免指数爆炸
return e_x / e_x.sum(axis=0)
def smooth(loss, cur_loss):
return loss * 0.999 + cur_loss * 0.001
def print_sample(sample_ix, ix_to_char):
'''
得到采样的索引对应的字符
sample_ix:采样字符的索引
ix_to_char:索引到字符的映射字典
'''
txt = ''.join(ix_to_char[ix] for ix in sample_ix) # 连接成字符串
txt = txt[0].upper() + txt[1:] # 首字母大写
print('%s' % (txt,), end='')
def get_initial_loss(vocab_size, seq_length):
return -np.log(1.0 / vocab_size) * seq_length
def initialize_parameters(n_a, n_x, n_y):
"""
用小随机数初始化模型参数
Returns:
parameters -- Python字典包含:
Wax -- 与输入相乘的权重矩阵, 维度 (n_a, n_x)
Waa -- 与之前隐藏状态相乘的权重矩阵, 维度 (n_a, n_a)
Wya -- 与当前隐藏状态相乘用于产生输出的权重矩阵, 维度(n_y,n_a)
ba -- 计算当前隐藏状态的偏置参数 维度 (n_a, 1)
by -- 计算当前输出的偏置参数 维度 (n_y, 1)
"""
np.random.seed(1)
Wax = np.random.randn(n_a, n_x) * 0.01
Waa = np.random.randn(n_a, n_a) * 0.01
Wya = np.random.randn(n_y, n_a) * 0.01
b = np.zeros((n_a, 1))
by = np.zeros((n_y, 1))
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
return parameters
### GRADED FUNCTION: clip
def clip(gradients, maxValue):
'''
把每个梯度值剪切到 minimum 和 maximum之间.
Arguments:
gradients -- Python梯度字典 包含 "dWaa", "dWax", "dWya", "db", "dby"
maxValue -- 每个大于maxValue或小于-maxValue的梯度值 被设置为该值
Returns:
gradients -- Python梯度字典 包含剪切后的切度
'''
# 取出梯度字典中存储的梯度
dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients[
'dby']
# 对每个梯度[dWax, dWaa, dWya, db, dby]进行剪切
for gradient in [dWax, dWaa, dWya, db, dby]:
# gradient[gradient>maxValue] = maxValue
# gradient[gradient<-maxValue] = -maxValue
np.clip(gradient, -maxValue, maxValue, out=gradient)
gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
return gradients
# GRADED FUNCTION: sample
def sample(parameters, char_to_ix, seed):
"""
根据朴素RNN输出的概率分布对字符序列进行采样
Arguments:
parameters --Python字典 包含模型参数 Waa, Wax, Wya, by, and b.
char_to_ix -- Python字典 把每个字符映射为索引
seed -- .
Returns:
indices -- 包含采样字符索引的列表.
"""
# 得到模型参数 和相关维度信息
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
vocab_size = by.shape[0] # 字典大小 输出单元的数量
n_a = Waa.shape[1] # 隐藏单元数量
# Step 1: 创建第一个时间步骤上输入的初始向量 初始化序列生成
x = np.zeros((vocab_size, 1))
# Step 1': 初始化a_prev
a_prev = np.zeros((n_a, 1))
# 保存生成字符index的列表
indices = []
# 检测换行符, 初始化为 -1
idx = -1
# 在每个时间步骤上进行循环.在每个时间步骤输出的概率分布上采样一个字符
# 把采样字典的index添加到indices中. 如果达到50个字符就停止 (说明模型训练有点问题)
# 用于终止无限循环 模型如果训练的不错的话 在遇到换行符之前不会达到50个字符
counter = 0
newline_character = char_to_ix['\n'] # 换行符索引
while (idx != newline_character and counter != 50): # 如果生成的字符不是换行符且循环次数小于50 就继续
# Step 2: 对x进行前向传播 公式(1), (2) and (3)
a = np.tanh(Wax.dot(x) + Waa.dot(a_prev) + b) # (n_a,1)
z = Wya.dot(a) + by # (n_y,1)
y = softmax(z) # (n_y,1)
np.random.seed(counter + seed)
# Step 3:从输出的概率分布y中 采样一个字典中的字符索引
idx = np.random.choice(range(vocab_size), p=y.ravel())
indices.append(idx)
# Step 4: 根据采样的索引 得到对应字符的one-hot形式 重写输入x
x = np.zeros((vocab_size, 1))
x[idx] = 1
# 更新a_prev
a_prev = a
seed += 1
counter += 1
if (counter == 50):
indices.append(char_to_ix['\n'])
return indices
def rnn_step_forward(parameters, a_prev, x):
'''朴素RNN单元的前行传播'''
# 从参数字典中取出参数
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
# 计算当前时间步骤上的隐藏状态
a_next = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
# 计算当前时间步骤上的预测输出 通过一个输出层(使用softmax激活函数,多分类 ,类别数为字典大小)
p_t = softmax(np.dot(Wya, a_next) + by)
return a_next, p_t
def rnn_step_backward(dy, gradients, parameters, x, a, a_prev):
'''朴素RNN单元的反向传播'''
gradients['dWya'] += np.dot(dy, a.T)
gradients['dby'] += dy
da = np.dot(parameters['Wya'].T, dy) + gradients['da_next'] # backprop into h
daraw = (1 - a * a) * da # backprop through tanh nonlinearity
gradients['db'] += daraw
gradients['dWax'] += np.dot(daraw, x.T)
gradients['dWaa'] += np.dot(daraw, a_prev.T)
gradients['da_next'] = np.dot(parameters['Waa'].T, daraw)
return gradients
def update_parameters(parameters, gradients, lr):
'''
使用随机梯度下降法更新模型参数
parameters:模型参数字典
gradients:对模型参数计算的梯度
lr:学习率
'''
parameters['Wax'] += -lr * gradients['dWax']
parameters['Waa'] += -lr * gradients['dWaa']
parameters['Wya'] += -lr * gradients['dWya']
parameters['b'] += -lr * gradients['db']
parameters['by'] += -lr * gradients['dby']
return parameters
def rnn_forward(X, Y, a0, parameters, vocab_size=27):
'''朴素RNN的前行传播
和上一个实验实验的RNN有所不同,之前我们一次处理m个样本/序列 要求m个序列有相同的长度
本次实验的RNN,一次只处理一个样本/序列(名字单词) 所以不用统一长度。
X -- 整数列表,每个数字代表一个字符的索引。 X是一个训练样本 代表一个单词
Y -- 整数列表,每个数字代表一个字符的索引。 Y是一个训练样本对应的真实标签 为X中的索引左移一位
'''
# Initialize x, a and y_hat as empty dictionaries
x, a, y_hat = {}, {}, {}
a[-1] = np.copy(a0)
# initialize your loss to 0
loss = 0
for t in range(len(X)):
# 设置x[t]为one-hot向量形式.
# 如果 X[t] == None, 设置 x[t]=0向量. 设置第一个时间步骤的输入为0向量
x[t] = np.zeros((vocab_size, 1)) # 设置每个时间步骤的输入向量
if (X[t] != None):
x[t][X[t]] = 1 # one-hot形式 索引位置为1 其余为0
# 运行一步RNN前向传播
a[t], y_hat[t] = rnn_step_forward(parameters, a[t - 1], x[t])
# 得到当前时间步骤的隐藏状态和预测输出
# 把预测输出和真实标签结合 计算交叉熵损失
loss -= np.log(y_hat[t][Y[t], 0])
cache = (y_hat, a, x)
return loss, cache
def rnn_backward(X, Y, parameters, cache):
'''朴素RNN的反向传播'''
# Initialize gradients as an empty dictionary
gradients = {}
# Retrieve from cache and parameters
(y_hat, a, x) = cache
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
# each one should be initialized to zeros of the same dimension as its corresponding parameter
gradients['dWax'], gradients['dWaa'], gradients['dWya'] = np.zeros_like(Wax), np.zeros_like(Waa), np.zeros_like(Wya)
gradients['db'], gradients['dby'] = np.zeros_like(b), np.zeros_like(by)
gradients['da_next'] = np.zeros_like(a[0])
### START CODE HERE ###
# Backpropagate through time
for t in reversed(range(len(X))):
dy = np.copy(y_hat[t])
dy[Y[t]] -= 1
gradients = rnn_step_backward(dy, gradients, parameters, x[t], a[t], a[t - 1])
### END CODE HERE ###
return gradients, a
# GRADED FUNCTION: optimize
def optimize(X, Y, a_prev, parameters, learning_rate=0.01):
"""
执行一步优化过程(随机梯度下降,一次优化使用一个训练训练).
Arguments:
X -- 整数列表,每个数字代表一个字符的索引。 X是一个训练样本 代表一个单词
Y -- 整数列表,每个数字代表一个字符的索引。 Y是一个训练样本对应的真实标签 为X中的索引左移一位
a_prev -- 上一个时间步骤产生的隐藏状态
parameters -- Python字典包含:
Wax -- 与输入相乘的权重矩阵, 维度 (n_a, n_x)
Waa -- 与之前隐藏状态相乘的权重矩阵, 维度 (n_a, n_a)
Wya -- 与当前隐藏状态相乘用于产生输出的权重矩阵, 维度 (n_y, n_a)
ba -- 计算当前隐藏状态的偏置参数 维度 (n_a, 1)
by -- 计算当前输出的偏置参数 维度 (n_y, 1)
learning_rate -- 学习率
Returns:
loss -- loss函数值(交叉熵)
gradients -- python dictionary containing:
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
db -- Gradients of bias vector, of shape (n_a, 1)
dby -- Gradients of output bias vector, of shape (n_y, 1)
a[len(X)-1] -- 最后一个隐藏状态 (n_a, 1)
"""
# 通过时间前向传播
loss, cache = rnn_forward(X, Y, a_prev, parameters, vocab_size=27)
# 通过时间的反向传播
gradients, a = rnn_backward(X, Y, parameters, cache)
# 梯度剪切 -5 (min) 5 (max)
gradients = clip(gradients, maxValue=5)
# 更新参数
parameters = update_parameters(parameters, gradients, lr=learning_rate)
return loss, gradients, a[len(X) - 1]
# GRADED FUNCTION: model
def model(data, ix_to_char, char_to_ix, num_iterations=35000, n_a=50, dino_names=7, vocab_size=27):
"""
训练模型生成恐龙名字.
Arguments:
data -- 文本语料(恐龙名字数据集)
ix_to_char -- 从索引到字符的映射字典
char_to_ix -- 从字符到索引的映射字典
num_iterations -- 随机梯度下降的迭代次数 每次使用一个训练样本(一个名字)
n_a -- RNN单元中的隐藏单元数
dino_names -- 采样的恐龙名字数量
vocab_size -- 字典的大小 文本语料中不同的字符数
Returns:
parameters -- 训练好的参数
"""
# 输入特征向量x的维度n_x, 输出预测概率向量的维度n_y 2者都为字典大小
n_x, n_y = vocab_size, vocab_size
# 初始化参数
parameters = initialize_parameters(n_a, n_x, n_y)
# 初始化loss (this is required because we want to smooth our loss, don't worry about it)
loss = get_initial_loss(vocab_size, dino_names)
# 得到所有恐龙名字的列表 (所有训练样本).
with open("D:/dinos.txt") as f:
examples = f.readlines() # 读取所有行 每行是一个名字 作为列表的一个元素
examples = [x.lower().strip() for x in examples] # 转换小写 去掉换行符
# 随机打乱所有恐龙名字 所有训练样本
np.random.seed(0)
np.random.shuffle(examples)
# 初始化隐藏状态为0
a_prev = np.zeros((n_a, 1))
# 优化循环
for j in range(num_iterations):
# 得到一个训练样本 (X,Y)
index = j % len(examples) # 得到随机打乱后的一个名字的索引
X = [None] + [char_to_ix[ch] for ch in examples[index]] # 把名字中的每个字符转为对应的索引 第一个字符为None翻译为0向量
Y = X[1:] + [char_to_ix['\n']]
# 随机梯度下降 执行一次优化: Forward-prop -> Backward-prop -> Clip -> Update parameters
# 学习率 0.01
curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate=0.01)
# 使用延迟技巧保持loss平稳. 加速训练
loss = smooth(loss, curr_loss)
# 每2000次随机梯度下降迭代, 通过sample()生成'n'个字符(1个名字) 来检查模型是否训练正确
if j % 2000 == 0:
print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
seed = 0
for name in range(dino_names): # 生成名字的数量
# 得到采样字符的索引
sampled_indices = sample(parameters, char_to_ix, seed)
# 得到索引对应的字符 生成一个名字
print_sample(sampled_indices, ix_to_char)
seed += 1 # To get the same result for grading purposed, increment the seed by one.
print('\n')
return parameters
parameters = model(data, ix_to_char, char_to_ix) #训练模型
下面翻译论文中的关键内容(自认为比较关键的):
模型的结构:
1. 初始化参数
2. 运行优化循环:前向传播计算loss、反向传播计算loss对于每个参数的梯度、梯度剪切避免梯度爆炸、利用计算的梯度,根据梯度下降法则进行参数更新
3. 返回训练好的参数
梯度剪切:
在本小节中我们将实现 clip函数,实现梯度剪切,该函数会在优化循环中被调用. 回想之前,我们的循环结构通常包含前向传播,计算cost,反向传播计算梯度,梯度下降法(高级优化方法)更新参数。现在,在更新参数之前,我们将运行梯度剪切来确保计算的梯度没有发生"梯度爆炸",就是变为一个非常大的值。
在接下来的实验中, 实现 clip函数, 输入一个梯度字典,如果发生了梯度爆炸的话,则返回一个剪切后的梯度。有不同的梯度剪切方式;我们将使用一个简单的逐元素剪切过程 ,梯度向量中的那个元素被剪切到位于某个范围内[-N, N]. 一般的,需要提供一个 maxValue (如 10). 如果梯度向量中的某个元素大于 10, 则把它赋值为10;并且如果某个元素小于 -10,则把它设置为-10. 如果它在-10和10之间的话,不变.
梯度下降:
本小节我们将实现一个随机梯度下降函数(使用梯度剪切).我们将一次使用一个训练样本(一个名字)进行训练,因此优化算法是随机梯度下降。
以下是RNN常见的优化步骤:
1. 通过RNN前向传播计算loss
2. 通过时间进行反向传播,计算loss对于每个参数的梯度
3. 如果有必要的话,进行梯度剪切
4. 使用梯度下降法(或高级优化方法)更新参数
结论:
我们可以看到我们的模型已经开始在训练结束时生成似乎合理的恐龙名字。 起初,它产生了随机字符,但最后你可以看到恐龙名字都很酷。 随意训练模型更长时间并调试一下超参数来查看是否可以获得更好的结果。 我们的实现产生了一些非常酷的名字,如maconucon,marloralus和macingsersaurus。 我们的模型学习到恐龙的名字往往以“saurus”,“don”,“aura”,“tor”等结尾。
如果模型没有产生一些酷炫的名字,不要完全归咎于模型 - 并非所有真正的恐龙名字听起来都很酷。 (例如,dromaeosauroides是一个真正的恐龙名称并且在训练集中。)但是这个模型应该给你一组候选名字,你可以从中选择最酷的!
本次试验使用了相对较小的数据集,因此我们可以在CPU上快速训练RNN。 训练英语语言模型需要更大的数据集,并且通常需要更多的计算,并且在GPU上运行数小时。 我们把模型运行了很长一段时间,到目前为止,生成的名字是非常棒的的,不可战胜的,凶猛的:Mangosaurus!
6. 分析“序列到序列”源代码(选做)
h0相当于初始隐状态输入,h是正常的输入,1、2、3、4分别是不同的隐状态进入到下一个RNN Cell中去,由上一个的隐状态向量和当前输入确定当前输出和隐状态向量输出,从而将“hello”翻译成了"ohlol".
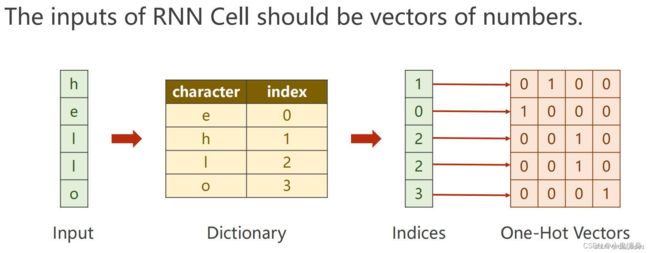
这是翻译的详细过程展示,其中有一个字典,我们按照这个字典对“hello进行编码”(这里是独热编码)得到的码片序列为:0100 1000 0010 0010 0001从而喂入数据进行运算,喂入之后,通过初始化隐状态向量和当前输入做隐状态向量的更新和当前的一个输出,再进行解码器按照字典对照表解码,从而输出第一个字母,依次类推,从而得到输出序列,这里我没有找到代码,所以没有做具体分析,只能按照图来分析其过程。
7. “编码器-解码器”的简单实现(必做)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
# enc_input(=input_batch): [batch_size, n_step+1, n_class]
# dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
完整代码:
# code by Tae Hwan Jung(Jeff Jung) @graykode, modify by wmathor
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# S: Symbol that shows starting of decoding input
# E: Symbol that shows starting of decoding output
# ?: Symbol that will fill in blank sequence if current batch data size is short than n_step
letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}
seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]
# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3
def make_data(seq_data):
enc_input_all, dec_input_all, dec_output_all = [], [], []
for seq in seq_data:
for i in range(2):
seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'
enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']
enc_input_all.append(np.eye(n_class)[enc_input])
dec_input_all.append(np.eye(n_class)[dec_input])
dec_output_all.append(dec_output) # not one-hot
# make tensor
return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)
'''
enc_input_all: [6, n_step+1 (because of 'E'), n_class]
dec_input_all: [6, n_step+1 (because of 'S'), n_class]
dec_output_all: [6, n_step+1 (because of 'E')]
'''
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)
class TranslateDataSet(Data.Dataset):
def __init__(self, enc_input_all, dec_input_all, dec_output_all):
self.enc_input_all = enc_input_all
self.dec_input_all = dec_input_all
self.dec_output_all = dec_output_all
def __len__(self): # return dataset size
return len(self.enc_input_all)
def __getitem__(self, idx):
return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]
loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
# enc_input(=input_batch): [batch_size, n_step+1, n_class]
# dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test
def translate(word):
enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
enc_input, dec_input = enc_input.to(device), dec_input.to(device)
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
hidden = torch.zeros(1, 1, n_hidden).to(device)
output = model(enc_input, hidden, dec_input)
# output : [n_step+1, batch_size, n_class]
predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
decoded = [letter[i] for i in predict]
translated = ''.join(decoded[:decoded.index('E')])
return translated.replace('?', '')
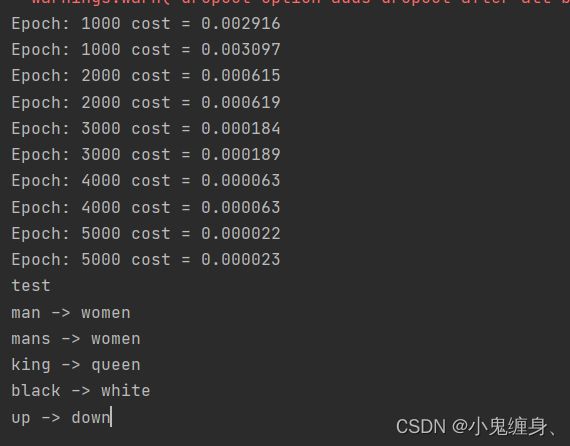
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))
总结
通过此次作业,我们使用numpy实现了一个SRN,(simple RNN),然后我们在已有的SRN基础上加入了激活函数,我们又用nn.RNNCell和nn.RNN实现了SRN。后来我们分析了二进制加法的源代码并且实现,做二进制加法这一块儿的翻译的时候,我体会到了编码器和解码器的作用,也看到了训练过程中的隐状态向量,使得我对RNN的理解更加深入,我们实现“Character-Level Language Models”源代码的时候,也是同样的思路,只不过比SRN更加的复杂,不容易理解,对于序列到序列的分析,因为没有找到代码,就看图分析了一下,感觉还是有一些代码是实现一些结果比较好,对于编码器和解码器的简单实现,我们参考了Seq2Seq 的 PyTorch 实现的代码,并详细读了他的代码,更加清楚的了解了Seq2Seq的整体结构,然后通过复现完整代码,体会过程,最后感觉收获还是很多的。今天就到这里,下边是参考博客:
References:
Seq2Seq 的 PyTorch 实现
吴恩达深度学习 | (22) 序列模型专项课程第一周编程作业实验2
Character level language model - Dinosaurus land
numpy 构建RNN和LSTM网络生成新的恐龙名字
NNDL 作业8:RNN - 简单循环网络