NNDL 作业8:RNN - 简单循环网络
NNDL 作业8:RNN - 简单循环网络
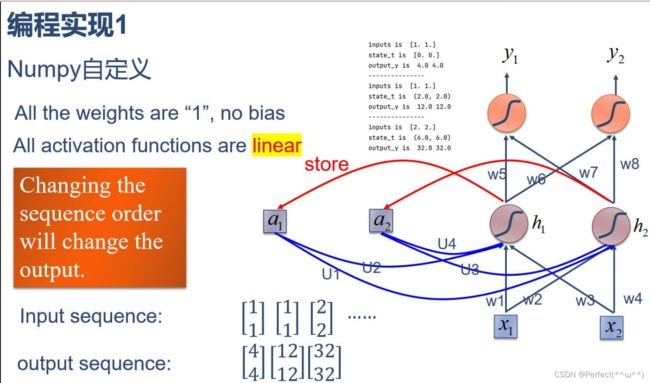
- 1. 使用Numpy实现SRN
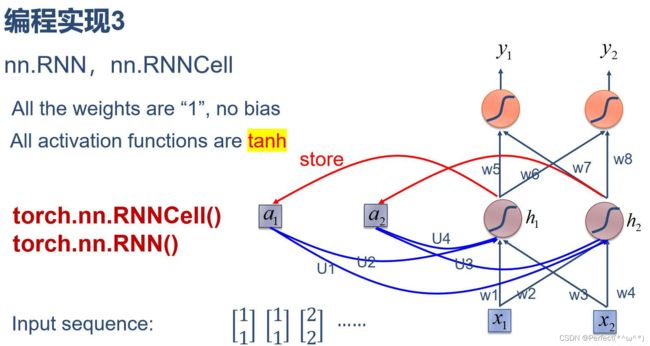
- 2. 在1的基础上,增加激活函数tanh
- 3. 分别使用nn.RNNCell、nn.RNN实现SRN
- 4. 分析“二进制加法” 源代码(选做)
- 5. 实现“Character-Level Language Models”源代码(必做)
- 6. 分析“序列到序列”源代码(选做)
- 7. “编码器-解码器”的简单实现(必做)
- 总结:
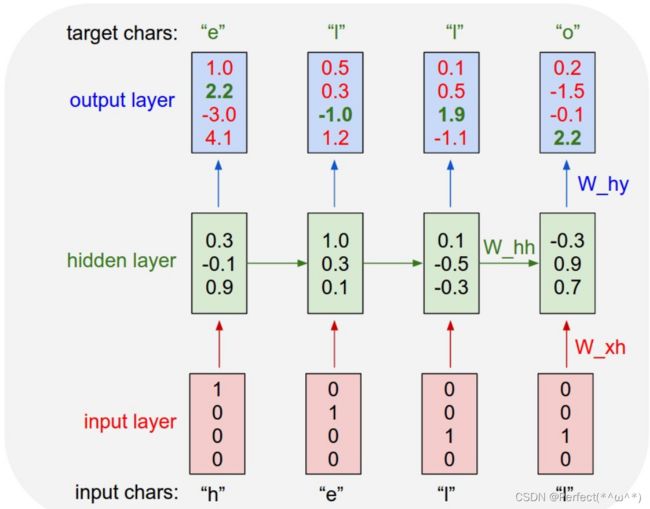
简单循环网络 ( Simple Recurrent Network , SRN) 只有一个隐藏层的神经网络
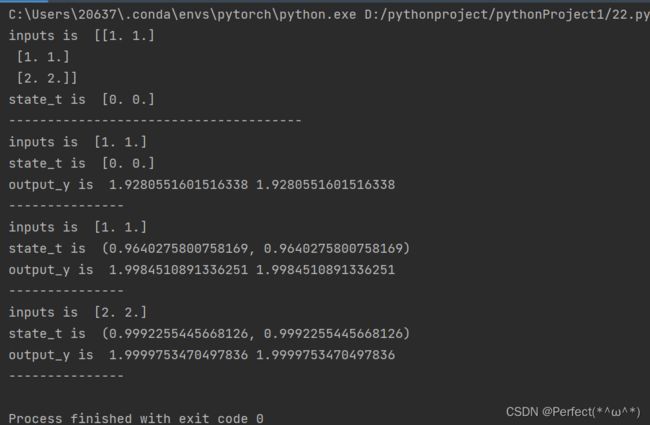
1. 使用Numpy实现SRN
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
2. 在1的基础上,增加激活函数tanh
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')
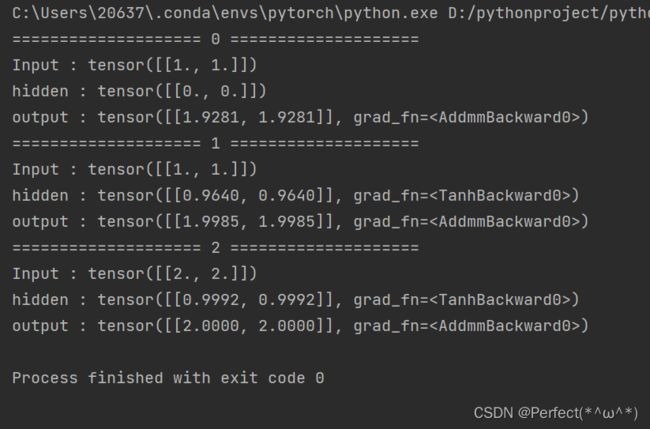
3. 分别使用nn.RNNCell、nn.RNN实现SRN
import torch
batch_size = 1
seq_len = 3 # 序列长度
input_size = 2 # 输入序列维度
hidden_size = 2 # 隐藏层维度
output_size = 2 # 输出层维度
# RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# 初始化参数 https://zhuanlan.zhihu.com/p/342012463
for name, param in cell.named_parameters():
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
seq = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(batch_size, hidden_size)
output = torch.zeros(batch_size, output_size)
for idx, input in enumerate(seq):
print('=' * 20, idx, '=' * 20)
print('Input :', input)
print('hidden :', hidden)
hidden = cell(input, hidden)
output = liner(hidden)
print('output :', output)
import torch
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
for name, param in cell.named_parameters(): # 初始化参数
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
inputs = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))
4. 分析“二进制加法” 源代码(选做)
import copy, numpy as np
np.random.seed(0)
#定义sigmoid函数
def sigmoid(x):
output = 1 / (1 + np.exp(-x))
return output
#定义sigmoid导数
def sigmoid_output_to_derivative(output):
return output * (1 - output)
#训练数据的产生
int2binary = {}
binary_dim = 8 #定义二进制位的长度
largest_number = pow(2, binary_dim)#定义数据的最大值
binary = np.unpackbits(
np.array([range(largest_number)], dtype=np.uint8).T, axis=1)#函数产生包装所有符合的二进制序列
for i in range(largest_number):#遍历从0-256的值
int2binary[i] = binary[i]#对于每个整型值赋值二进制序列
print(int2binary)
# 产生输入变量
alpha = 0.1 #设置更新速度(学习率)
input_dim = 2 #输入维度大小
hidden_dim = 16 #隐藏层维度大小
output_dim = 1 #输出维度大小
# 随机产生网络权重
synapse_0 = 2 * np.random.random((input_dim, hidden_dim)) - 1
synapse_1 = 2 * np.random.random((hidden_dim, output_dim)) - 1
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1
#梯度初始值设置为0
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)
#训练逻辑
for j in range(10000):
# 产生一个简单的加法问题
a_int = np.random.randint(largest_number / 2) # 产生一个加法操作数
a = int2binary[a_int] # 找到二进制序列编码
b_int = np.random.randint(largest_number / 2) # 产生另一个加法操作数
b = int2binary[b_int] # 找到二进制序列编码
# 计算正确值(标签值)
c_int = a_int + b_int
c = int2binary[c_int] # 得到正确的结果序列
# 设置存储器,存储中间值(记忆功能)
d = np.zeros_like(c)
overallError = 0 #设置误差
layer_2_deltas = list()
layer_1_values = list()
layer_1_values.append(np.zeros(hidden_dim))
# moving along the positions in the binary encoding
for position in range(binary_dim):
# 产生输入和输出
X = np.array([[a[binary_dim - position - 1], b[binary_dim - position - 1]]])
y = np.array([[c[binary_dim - position - 1]]]).T
# 隐藏层计算
layer_1 = sigmoid(np.dot(X, synapse_0) + np.dot(layer_1_values[-1], synapse_h))
# 输出层
layer_2 = sigmoid(np.dot(layer_1, synapse_1))
# 计算差别
layer_2_error = y - layer_2
#计算每个梯度
layer_2_deltas.append((layer_2_error) * sigmoid_output_to_derivative(layer_2))
#计算所有损失
overallError += np.abs(layer_2_error[0])
# 编码记忆的中间值
d[binary_dim - position - 1] = np.round(layer_2[0][0])
# 拷贝副本
layer_1_values.append(copy.deepcopy(layer_1))
future_layer_1_delta = np.zeros(hidden_dim)
for position in range(binary_dim):
X = np.array([[a[position], b[position]]])
layer_1 = layer_1_values[-position - 1]
prev_layer_1 = layer_1_values[-position - 2]
# 输出层误差
layer_2_delta = layer_2_deltas[-position - 1]
# 隐藏层误差
layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(
synapse_1.T)) * sigmoid_output_to_derivative(layer_1)
# 计算梯度
synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
synapse_0_update += X.T.dot(layer_1_delta)
future_layer_1_delta = layer_1_delta
#梯度下降
synapse_0 += synapse_0_update * alpha
synapse_1 += synapse_1_update * alpha
synapse_h += synapse_h_update * alpha
#重新初始化
synapse_0_update *= 0
synapse_1_update *= 0
synapse_h_update *= 0
# 打印训练过程
if (j % 1000 == 0):
print("Error:" + str(overallError))
print("Pred:" + str(d))
print("True:" + str(c))
out = 0
for index, x in enumerate(reversed(d)):
out += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out))
print("------------")
结果:

分析:首先,源代码中定义了两个函数:sigmoid函数和sigmoid导数函数,其次,我们产生0-256的8位二进制编码序列,并包装成一个字典,作为编码器,然后,我们设置训练过程中参数alpha和输入大小、隐藏层维度大小、输出维度大小等,并初始化网络权重,最后,我们对其进行训练,计算梯度,进行梯度下降法更新,中间设置存储器记录中间值,作为隐含变量输入,并将下一次的隐含变量同样进行梯度更新。我们打印几个训练中的例子,观察训练过程。
5. 实现“Character-Level Language Models”源代码(必做)
import numpy as np
import random
#utils.py中定义了本次实验所需要的辅助函数
#包括朴素RNN的前向/反向传播 和我们在上一个实验中实现的差不多
from utils import *
data = open('D:/dinos.txt', 'r').read() #读取dinos.txt中的所有恐龙名字 read()逐字符读取 返回一个字符串
data= data.lower()#把所有名字转为小写
chars = list(set(data))#得到字符列表并去重
print(chars) #'a'-'z' '\n' 27个字符
data_size, vocab_size = len(data), len(chars)
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))
char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }
ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }
print(ix_to_char)
def softmax(x):
''''softmax激活函数'''
e_x = np.exp(x - np.max(x)) # 首先对输入做一个平移 减去最大值 使其最大值为0 再取exp 避免指数爆炸
return e_x / e_x.sum(axis=0)
def smooth(loss, cur_loss):
return loss * 0.999 + cur_loss * 0.001
def print_sample(sample_ix, ix_to_char):
'''
得到采样的索引对应的字符
sample_ix:采样字符的索引
ix_to_char:索引到字符的映射字典
'''
txt = ''.join(ix_to_char[ix] for ix in sample_ix) # 连接成字符串
txt = txt[0].upper() + txt[1:] # 首字母大写
print('%s' % (txt,), end='')
def get_initial_loss(vocab_size, seq_length):
return -np.log(1.0 / vocab_size) * seq_length
def initialize_parameters(n_a, n_x, n_y):
"""
用小随机数初始化模型参数
Returns:
parameters -- Python字典包含:
Wax -- 与输入相乘的权重矩阵, 维度 (n_a, n_x)
Waa -- 与之前隐藏状态相乘的权重矩阵, 维度 (n_a, n_a)
Wya -- 与当前隐藏状态相乘用于产生输出的权重矩阵, 维度(n_y,n_a)
ba -- 计算当前隐藏状态的偏置参数 维度 (n_a, 1)
by -- 计算当前输出的偏置参数 维度 (n_y, 1)
"""
np.random.seed(1)
Wax = np.random.randn(n_a, n_x) * 0.01
Waa = np.random.randn(n_a, n_a) * 0.01
Wya = np.random.randn(n_y, n_a) * 0.01
b = np.zeros((n_a, 1))
by = np.zeros((n_y, 1))
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
return parameters
### GRADED FUNCTION: clip
def clip(gradients, maxValue):
'''
把每个梯度值剪切到 minimum 和 maximum之间.
Arguments:
gradients -- Python梯度字典 包含 "dWaa", "dWax", "dWya", "db", "dby"
maxValue -- 每个大于maxValue或小于-maxValue的梯度值 被设置为该值
Returns:
gradients -- Python梯度字典 包含剪切后的切度
'''
# 取出梯度字典中存储的梯度
dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients[
'dby']
# 对每个梯度[dWax, dWaa, dWya, db, dby]进行剪切
for gradient in [dWax, dWaa, dWya, db, dby]:
# gradient[gradient>maxValue] = maxValue
# gradient[gradient<-maxValue] = -maxValue
np.clip(gradient, -maxValue, maxValue, out=gradient)
gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
return gradients
# GRADED FUNCTION: sample
def sample(parameters, char_to_ix, seed):
"""
根据朴素RNN输出的概率分布对字符序列进行采样
Arguments:
parameters --Python字典 包含模型参数 Waa, Wax, Wya, by, and b.
char_to_ix -- Python字典 把每个字符映射为索引
seed -- .
Returns:
indices -- 包含采样字符索引的列表.
"""
# 得到模型参数 和相关维度信息
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
vocab_size = by.shape[0] # 字典大小 输出单元的数量
n_a = Waa.shape[1] # 隐藏单元数量
# Step 1: 创建第一个时间步骤上输入的初始向量 初始化序列生成
x = np.zeros((vocab_size, 1))
# Step 1': 初始化a_prev
a_prev = np.zeros((n_a, 1))
# 保存生成字符index的列表
indices = []
# 检测换行符, 初始化为 -1
idx = -1
# 在每个时间步骤上进行循环.在每个时间步骤输出的概率分布上采样一个字符
# 把采样字典的index添加到indices中. 如果达到50个字符就停止 (说明模型训练有点问题)
# 用于终止无限循环 模型如果训练的不错的话 在遇到换行符之前不会达到50个字符
counter = 0
newline_character = char_to_ix['\n'] # 换行符索引
while (idx != newline_character and counter != 50): # 如果生成的字符不是换行符且循环次数小于50 就继续
# Step 2: 对x进行前向传播 公式(1), (2) and (3)
a = np.tanh(Wax.dot(x) + Waa.dot(a_prev) + b) # (n_a,1)
z = Wya.dot(a) + by # (n_y,1)
y = softmax(z) # (n_y,1)
np.random.seed(counter + seed)
# Step 3:从输出的概率分布y中 采样一个字典中的字符索引
idx = np.random.choice(range(vocab_size), p=y.ravel())
indices.append(idx)
# Step 4: 根据采样的索引 得到对应字符的one-hot形式 重写输入x
x = np.zeros((vocab_size, 1))
x[idx] = 1
# 更新a_prev
a_prev = a
seed += 1
counter += 1
if (counter == 50):
indices.append(char_to_ix['\n'])
return indices
def rnn_step_forward(parameters, a_prev, x):
'''朴素RNN单元的前行传播'''
# 从参数字典中取出参数
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
# 计算当前时间步骤上的隐藏状态
a_next = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
# 计算当前时间步骤上的预测输出 通过一个输出层(使用softmax激活函数,多分类 ,类别数为字典大小)
p_t = softmax(np.dot(Wya, a_next) + by)
return a_next, p_t
def rnn_step_backward(dy, gradients, parameters, x, a, a_prev):
'''朴素RNN单元的反向传播'''
gradients['dWya'] += np.dot(dy, a.T)
gradients['dby'] += dy
da = np.dot(parameters['Wya'].T, dy) + gradients['da_next'] # backprop into h
daraw = (1 - a * a) * da # backprop through tanh nonlinearity
gradients['db'] += daraw
gradients['dWax'] += np.dot(daraw, x.T)
gradients['dWaa'] += np.dot(daraw, a_prev.T)
gradients['da_next'] = np.dot(parameters['Waa'].T, daraw)
return gradients
def update_parameters(parameters, gradients, lr):
'''
使用随机梯度下降法更新模型参数
parameters:模型参数字典
gradients:对模型参数计算的梯度
lr:学习率
'''
parameters['Wax'] += -lr * gradients['dWax']
parameters['Waa'] += -lr * gradients['dWaa']
parameters['Wya'] += -lr * gradients['dWya']
parameters['b'] += -lr * gradients['db']
parameters['by'] += -lr * gradients['dby']
return parameters
def rnn_forward(X, Y, a0, parameters, vocab_size=27):
'''朴素RNN的前行传播
和上一个实验实验的RNN有所不同,之前我们一次处理m个样本/序列 要求m个序列有相同的长度
本次实验的RNN,一次只处理一个样本/序列(名字单词) 所以不用统一长度。
X -- 整数列表,每个数字代表一个字符的索引。 X是一个训练样本 代表一个单词
Y -- 整数列表,每个数字代表一个字符的索引。 Y是一个训练样本对应的真实标签 为X中的索引左移一位
'''
# Initialize x, a and y_hat as empty dictionaries
x, a, y_hat = {}, {}, {}
a[-1] = np.copy(a0)
# initialize your loss to 0
loss = 0
for t in range(len(X)):
# 设置x[t]为one-hot向量形式.
# 如果 X[t] == None, 设置 x[t]=0向量. 设置第一个时间步骤的输入为0向量
x[t] = np.zeros((vocab_size, 1)) # 设置每个时间步骤的输入向量
if (X[t] != None):
x[t][X[t]] = 1 # one-hot形式 索引位置为1 其余为0
# 运行一步RNN前向传播
a[t], y_hat[t] = rnn_step_forward(parameters, a[t - 1], x[t])
# 得到当前时间步骤的隐藏状态和预测输出
# 把预测输出和真实标签结合 计算交叉熵损失
loss -= np.log(y_hat[t][Y[t], 0])
cache = (y_hat, a, x)
return loss, cache
def rnn_backward(X, Y, parameters, cache):
'''朴素RNN的反向传播'''
# Initialize gradients as an empty dictionary
gradients = {}
# Retrieve from cache and parameters
(y_hat, a, x) = cache
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
# each one should be initialized to zeros of the same dimension as its corresponding parameter
gradients['dWax'], gradients['dWaa'], gradients['dWya'] = np.zeros_like(Wax), np.zeros_like(Waa), np.zeros_like(Wya)
gradients['db'], gradients['dby'] = np.zeros_like(b), np.zeros_like(by)
gradients['da_next'] = np.zeros_like(a[0])
### START CODE HERE ###
# Backpropagate through time
for t in reversed(range(len(X))):
dy = np.copy(y_hat[t])
dy[Y[t]] -= 1
gradients = rnn_step_backward(dy, gradients, parameters, x[t], a[t], a[t - 1])
### END CODE HERE ###
return gradients, a
# GRADED FUNCTION: optimize
def optimize(X, Y, a_prev, parameters, learning_rate=0.01):
"""
执行一步优化过程(随机梯度下降,一次优化使用一个训练训练).
Arguments:
X -- 整数列表,每个数字代表一个字符的索引。 X是一个训练样本 代表一个单词
Y -- 整数列表,每个数字代表一个字符的索引。 Y是一个训练样本对应的真实标签 为X中的索引左移一位
a_prev -- 上一个时间步骤产生的隐藏状态
parameters -- Python字典包含:
Wax -- 与输入相乘的权重矩阵, 维度 (n_a, n_x)
Waa -- 与之前隐藏状态相乘的权重矩阵, 维度 (n_a, n_a)
Wya -- 与当前隐藏状态相乘用于产生输出的权重矩阵, 维度 (n_y, n_a)
ba -- 计算当前隐藏状态的偏置参数 维度 (n_a, 1)
by -- 计算当前输出的偏置参数 维度 (n_y, 1)
learning_rate -- 学习率
Returns:
loss -- loss函数值(交叉熵)
gradients -- python dictionary containing:
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
db -- Gradients of bias vector, of shape (n_a, 1)
dby -- Gradients of output bias vector, of shape (n_y, 1)
a[len(X)-1] -- 最后一个隐藏状态 (n_a, 1)
"""
# 通过时间前向传播
loss, cache = rnn_forward(X, Y, a_prev, parameters, vocab_size=27)
# 通过时间的反向传播
gradients, a = rnn_backward(X, Y, parameters, cache)
# 梯度剪切 -5 (min) 5 (max)
gradients = clip(gradients, maxValue=5)
# 更新参数
parameters = update_parameters(parameters, gradients, lr=learning_rate)
return loss, gradients, a[len(X) - 1]
# GRADED FUNCTION: model
def model(data, ix_to_char, char_to_ix, num_iterations=35000, n_a=50, dino_names=7, vocab_size=27):
"""
训练模型生成恐龙名字.
Arguments:
data -- 文本语料(恐龙名字数据集)
ix_to_char -- 从索引到字符的映射字典
char_to_ix -- 从字符到索引的映射字典
num_iterations -- 随机梯度下降的迭代次数 每次使用一个训练样本(一个名字)
n_a -- RNN单元中的隐藏单元数
dino_names -- 采样的恐龙名字数量
vocab_size -- 字典的大小 文本语料中不同的字符数
Returns:
parameters -- 训练好的参数
"""
# 输入特征向量x的维度n_x, 输出预测概率向量的维度n_y 2者都为字典大小
n_x, n_y = vocab_size, vocab_size
# 初始化参数
parameters = initialize_parameters(n_a, n_x, n_y)
# 初始化loss (this is required because we want to smooth our loss, don't worry about it)
loss = get_initial_loss(vocab_size, dino_names)
# 得到所有恐龙名字的列表 (所有训练样本).
with open("D:/dinos.txt") as f:
examples = f.readlines() # 读取所有行 每行是一个名字 作为列表的一个元素
examples = [x.lower().strip() for x in examples] # 转换小写 去掉换行符
# 随机打乱所有恐龙名字 所有训练样本
np.random.seed(0)
np.random.shuffle(examples)
# 初始化隐藏状态为0
a_prev = np.zeros((n_a, 1))
# 优化循环
for j in range(num_iterations):
# 得到一个训练样本 (X,Y)
index = j % len(examples) # 得到随机打乱后的一个名字的索引
X = [None] + [char_to_ix[ch] for ch in examples[index]] # 把名字中的每个字符转为对应的索引 第一个字符为None翻译为0向量
Y = X[1:] + [char_to_ix['\n']]
# 随机梯度下降 执行一次优化: Forward-prop -> Backward-prop -> Clip -> Update parameters
# 学习率 0.01
curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate=0.01)
# 使用延迟技巧保持loss平稳. 加速训练
loss = smooth(loss, curr_loss)
# 每2000次随机梯度下降迭代, 通过sample()生成'n'个字符(1个名字) 来检查模型是否训练正确
if j % 2000 == 0:
print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
seed = 0
for name in range(dino_names): # 生成名字的数量
# 得到采样字符的索引
sampled_indices = sample(parameters, char_to_ix, seed)
# 得到索引对应的字符 生成一个名字
print_sample(sampled_indices, ix_to_char)
seed += 1 # To get the same result for grading purposed, increment the seed by one.
print('\n')
return parameters
parameters = model(data, ix_to_char, char_to_ix) #训练模型
翻译Character-Level Language Models 相关内容:
RNN计算。那么这些东西是如何工作的呢?在核心,RNN有一个看似简单的API:它们接受一个输入向量x,并给你一个输出向量y。然而,至关重要的是,这个输出向量的内容不仅受到你刚刚输入的输入的影响,还受到你过去输入的整个历史的影响。作为类编写,RNN的API由一个单步函数组成:
rnn = RNN()
y = rnn.step(x) # x is an input vector, y is the RNN's output vector
RNN类有一些内部状态,每次调用步骤时都会更新。在最简单的情况下,该状态由单个隐藏向量h组成。下面是Vanilla RNN中的步进函数的实现:
class RNN:
# ...
def step(self, x):
# update the hidden state
self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))
# compute the output vector
y = np.dot(self.W_hy, self.h)
return y
上面指定了香草 RNN 的前向传递。这个RNN的参数是三个矩阵。隐藏状态使用零向量初始化。该函数实现了将激活压缩到范围的非线性。简要注意这是如何工作的:tanh 中有两个项:一个基于先前的隐藏状态,另一个基于当前输入。在 numpyis 矩阵乘法中。两个中间体与加法相互作用,然后被tanh挤压到新的状态向量中。如果你对数学符号更熟悉,我们也可以把隐藏状态更新写成W_hh, W_xh, W_hyself.hnp.tanh[-1, 1]np.dotht=谭(WHhhht−1+Wx高xt),其中 tanh 是按元素应用的。
有效框架的可取特征是:
- CPU/GPU透明Tensor库,具有大量功能(切片、数组/矩阵操作等)
- 脚本语言(理想情况下为Python)中的一个完全独立的代码库,它在Tensor上运行并实现所有深度学习内容。
- 应该可以轻松地共享预训练模型
- 没有编译步骤。深度学习的趋势是向更大、更复杂的网络发展,这些网络以复杂的图形进行时间展开。很关键的是,这些代码不能长时间编译,否则开发时间会受到很大影响。其次,通过编译,放弃了可解释性和有效记录/调试的能力。如果为了提高生产效率而开发了图形,那么可以选择编译该图形。
6. 分析“序列到序列”源代码(选做)
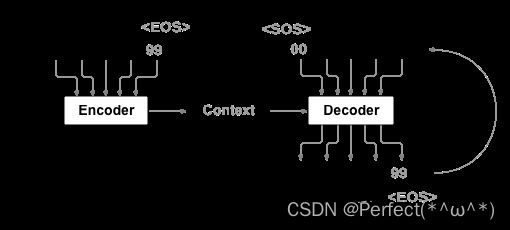
首先,从上面的图可以很明显的看出,Seq2Seq 需要对三个变量进行操作,这和之前我接触到的所有网络结构都不一样。我们把 Encoder 的输入称为 enc_input,Decoder 的输入称为 dec_input, Decoder 的输出称为 dec_output。
也可以通过这个图了解一下:

7. “编码器-解码器”的简单实现(必做)
# code by Tae Hwan Jung(Jeff Jung) @graykode, modify by wmathor
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# S: Symbol that shows starting of decoding input
# E: Symbol that shows starting of decoding output
# ?: Symbol that will fill in blank sequence if current batch data size is short than n_step
letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}
seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]
# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3
def make_data(seq_data):
enc_input_all, dec_input_all, dec_output_all = [], [], []
for seq in seq_data:
for i in range(2):
seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'
enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']
enc_input_all.append(np.eye(n_class)[enc_input])
dec_input_all.append(np.eye(n_class)[dec_input])
dec_output_all.append(dec_output) # not one-hot
# make tensor
return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)
'''
enc_input_all: [6, n_step+1 (because of 'E'), n_class]
dec_input_all: [6, n_step+1 (because of 'S'), n_class]
dec_output_all: [6, n_step+1 (because of 'E')]
'''
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)
class TranslateDataSet(Data.Dataset):
def __init__(self, enc_input_all, dec_input_all, dec_output_all):
self.enc_input_all = enc_input_all
self.dec_input_all = dec_input_all
self.dec_output_all = dec_output_all
def __len__(self): # return dataset size
return len(self.enc_input_all)
def __getitem__(self, idx):
return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]
loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
# enc_input(=input_batch): [batch_size, n_step+1, n_class]
# dec_inpu(=output_batch): [batch_size, n_step+1, n_class]
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (
enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test
def translate(word):
enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
enc_input, dec_input = enc_input.to(device), dec_input.to(device)
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
hidden = torch.zeros(1, 1, n_hidden).to(device)
output = model(enc_input, hidden, dec_input)
# output : [n_step+1, batch_size, n_class]
predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
decoded = [letter[i] for i in predict]
translated = ''.join(decoded[:decoded.index('E')])
return translated.replace('?', '')
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))
总结:
本次作业主要是关于RNN - 简单循环网络的一些东西。首先是使用Numpy实现SRN,其次又在此基础上加入了激活函数tanh。然后又分别使用nn.RNNCell、nn.RNN实现了SRN;完成了实现“Character-Level Language Models”源代码;完成了“编码器-解码器”的简单实现。之前一直不知道循环记忆神经网络是如何完成自我输入的,通过这次实验,我看到了他的代码结构,明白了神经元如何实现“记忆”的,感受很多,收获颇多。