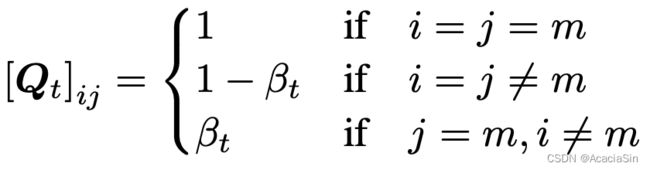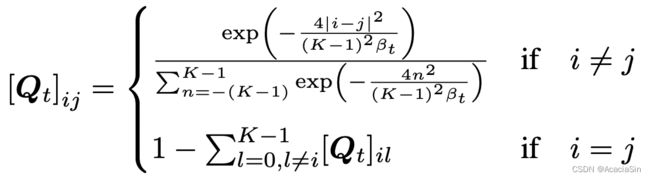Structured Denoising Diffusion Models in Discrete State-Spaces【D3PM重点笔记】
Structured Denoising Diffusion Models in Discrete State-Spaces离散状态空间中的结构化去噪扩散模型笔记
摘要
本文:
- 引入了离散去噪扩散概率模型D3PMS ,其退化包括了:
- 在连续空间中模仿高斯核的过渡矩阵的退化
- 基于嵌入空间embedding space中最近邻的矩阵
- 引入吸收状态的矩阵
- 说明了过渡矩阵的选择非常重要,导致了文本和图像的改进结果
- 引入了新的损失函数,该函数将变分下限与辅助交叉熵损失结合起来。
本文结果:
- 文本:字符级文本生成取得了良好的结果
- 图像:接近样本质量,并超过了连续空间DDPM模型的对数可能性
1 引言
这项工作的目的:
- 通过使用一个更加结构化的分类退化过程来塑造数据生成、改进和拓展离散扩散模型
- 不需要将离散数据嵌入到连续空间
- 可以将结构或领域知识嵌入到正向过程的过渡矩阵中
作者:
- 开发了适合文本数据的结构化退化过程
- 探索了插入[MASK]标记的退化过程
- 量化了图像的离散扩散模型(优先扩散到更多相似状态)
- 引入了新的辅助损失,稳定了D3PMS的训练
- 引入了一系列基于相互信息的噪声计划,提高了性能
- 成功地将离散扩散模型拓展到大词汇量和长序列长度。
2 背景:Diffusion Models
回顾了Diffusion Models的前向过程和逆向过程,以及其对应的表达式。
3 离散状态空间的扩散模型
我们简要地描诉了一个更普遍的分类随机变量扩散框架:
对于具有K个类别的标量离散随机变量 x t , x t − 1 x_t,x_{t-1} xt,xt−1,他们的前向转移概率,可以用矩阵表示:
[ Q t ] i j = q ( x t = j ∣ x t − 1 = i ) [Q_t]_{ij}= q(x_t=j|x_{t-1}=i) [Qt]ij=q(xt=j∣xt−1=i)
用行向量 x \mathrm{x} x来表示 x x x的one-hot向量,则可以把概率改写为:
q ( x t ∣ x t − 1 ) = C a t ( x t ; p = x t − 1 Q t ) q(\mathrm{x_t}|\mathrm{x_{t-1}}) = Cat(\mathrm{x_t};p=\mathrm{x_{t-1}}Q_t) q(xt∣xt−1)=Cat(xt;p=xt−1Qt)
从而推理得到 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)的计算公式,并且证明了如何在大K和大T时计算得到 Q t ‾ \overline{Q_t} Qt
3.1 前向过程的马尔可夫过渡矩阵的选择
D3PM框架的一个优点是:能通过选择 Q t Q_t Qt来控制数据损坏和去噪过程。
选择 Q t Q_t Qt的约束有两点:
- Q t Q_t Qt所有行必须和为1
- Q t ‾ = Q 1 Q 2 . . . Q t \overline{Q_t}=Q_1Q_2...Q_t Qt=Q1Q2...Qt,当 t t t变大时,必须收敛到一个已知的静止的分布。
为了控制前向corruption过程和可学习的反响去燥过程,向过渡矩阵 Q t Q_t Qt添加domain-dependent structure领域依赖性结构是有意义的。矩阵类型有:
Uniform均匀:具有严格正项的双重随机性。最终收敛得到的分布是均匀的。
Abosrbing state吸收状态:每个标记要么保持不变,要么以某种概率t过渡到[MASK]。最终收敛得到的分布不是均匀的,而且在[MASK]标记上不同的。对于图像,使用灰色像素作为[MASK]吸收标记。
Discretized Gaussian离散高斯:对于有顺序的数据,使用离散的、截断的高斯分布来模仿连续空间扩散模型,过渡矩阵是双重随机的,且以跟高的概率在更多相似的状态之间过渡,适合量化的序数数据,如图像。最终收敛得到的分布是均匀的。
Token embedding distance Token embedding的距离:文本数据没有序数结构,但有语义关系。在前向过程中,使用词嵌入空间中的相似性来指导前向过程,构建了一个双重随机性的过渡矩阵。最终收敛得到的分布是均匀的。
3.2 噪声方案
前向过程中,几种不同的噪声方案:
- 离散的高斯扩散:在离散化之前现行的增加高斯的方差
- 均匀扩散:将过渡矩阵的累积概率设置为余弦函数
- 一般的过渡矩阵(如基于token嵌入的矩阵):将 x t x_t xt和 x 0 x_0 x0之间的相互信息线性内插为0。
3.3 反向过程的参数化(logP p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)的优化过程?)
跟随HO等人,使用神经网络预测了 p θ ~ ( x 0 ~ ∣ x t ) \widetilde{p_\theta}(\widetilde{x_0}|x_t) pθ (x0 ∣xt)的对数的分布,得到了一个参数化的过程。在这个参数化的过程下,有可能导致KL值为0.
再根据前面 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)的表示,得知最优的反向过程,只考虑了 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)是非零的情况。
由上可得, Q t Q_t Qt的稀疏模式决定了 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)最理想的逆向转换概率。而跟随HO等人的参数化过程也确保了学习到的反向概率分布 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt) 具有正确的稀疏模式。
最后,这种参数化能够让我们一次进行k步推理,在预测 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}|x_t) pθ(xt−1∣xt)的过程中。
最后作者提出,在建立有序离散数据的模型时,与其直接用神经网络的输出来预测 p θ ~ ( x 0 ~ ∣ x t ) \widetilde{p_\theta}(\widetilde{x_0}|x_t) pθ (x0 ∣xt)的对数的,不如用截断的离散的对数分布来模拟概率。这样做还能提高图像的FID的分数和log-likelihood分数。
3.4 损失函数
我们为反向过程的 x 0 x_0 x0参数化引入了一个辅助去噪目标。新的Loss函数 L λ L_\lambda Lλ直接监督了模型的输出 p θ ~ ( x 0 ~ ∣ x t ) \widetilde{p_\theta}(\widetilde{x_0}|x_t) pθ (x0 ∣xt)。用这种损失进行训练可以提高图像样本的质量。
4 与现有文本概率模型的联系
通过公式变换,说明了BERT、自回归模型,(生成式)Masked Language-Models这三类模型都是扩散模型。
5 文本生成
作者在两个数据集text8和LM1B上,训练了三个模型:
- D3PM Uniform
- D3PM absorbing
- D3PM NN
5.1 文本上的字符级生成8
结果显示,D3PM absorbing模型的表现最好,远超于Uniform 和 NN的模型。且当L=0.01时对D3PM Absorbing效果最好,Lvb对D3PM Uniform效果最好。
5.2 在LM1B上生成文本
结果显示,D3PM absorbing模型的表现最好。且当L=0.01时对D3PM Absorbing效果最好。不仅如此,复杂度大大降低,在推理步骤少于10步时就取得了很好的效果。
6 图像生成
用数据姐CIFAR-10来评估三个模型:
- D3PM uniform
- D3PM absorbing
- D3PM Gauss
最佳结果:D3PM Guass+用 L λ L_\lambda Lλ训练+在反向过程中用截断对数参数化的分布模拟。
λ = 0.001 \lambda=0.001 λ=0.001时效果最好
7 相关工作
一些相关工作
8 讨论
D3PMS是通过定义新的离散退化过程来改进离散数据的扩散模型,比之前提出的离散扩散模型实验结果好得多。甚至在图像生成的ll上超过了连续扩散模型的性能。但文本生成方面仍然比不上Transformer XL这样的强回归模型。
D3PM的进一步发展:
- 研究替代损失
- D3PM可能会从增加时间步数和更优化的噪声方案中受益
- D3PM受限制于现有的评价指标(一些评价生成模型的标准,如FID、IS等)
未来可以有更多的可能性,可以利用更加丰富的结构形式来定义更强大的离散扩散模型。