Diffusion Models - 扩散模型（一）

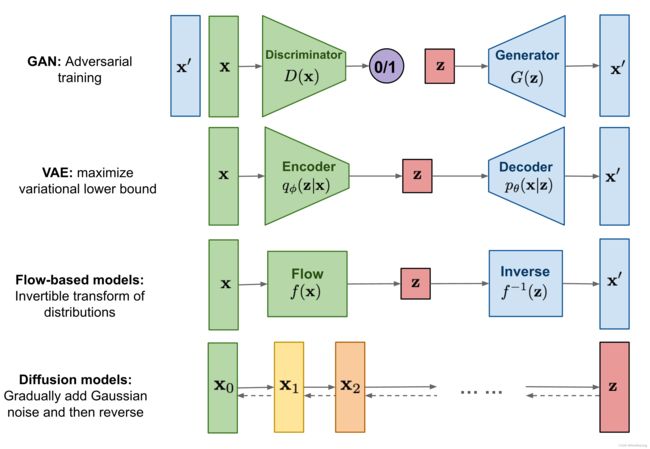
常见的生成模型（Generative Models）如 GAN、VAE 和基于流( Flow-based )的模型。他们在生成高质量样本方面取得了巨大成功，但每个都有其自身的局限性。 GAN 因其对抗性训练性质，其训练过程难以收敛以及生成多样性欠佳。 VAE 依赖于替代损失（surrogate loss）。流模型必须使用专门的架构来构建可逆变换。

扩散模型( Diffusion Models )的灵感来自非平衡热力学。定义了扩散步骤的马尔可夫链，以缓慢地将随机噪声添加到数据中，然后学习逆向扩散过程以从噪声中构造所需的数据样本。与 VAE 或流模型不同，扩散模型是通过固定过程学习的，并且潜在变量具有高维度（与原始数据相同）。

图 1. 不同类型的生成模型概述。

1. Diffusion Models

已经提出了几种基于扩散的生成模型，其中包含类似的思想，包括

• 扩散概率模型（diffusion probabilistic models）：https://arxiv.org/abs/1503.03585
• 噪声条件评分网络（noise-conditioned score network）： https://arxiv.org/abs/1907.05600
• 去噪扩散概率模型（denoising diffusion probabilistic models）： https://arxiv.org/abs/2006.11239

1.1 Forward diffusion process

给定从真实数据分布中采样的数据点 ${\mathbf{x}}_0\sim q(\mathbf{x})$ ，定义一个前向扩散过程，其中在 $T$ 步中向样本添加少量高斯噪声，产生一系列噪声样本 ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_T$ 。步长由方差表控制 $\{{\beta }_t\in (0,1){\}}_{t=1}^T$

$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$$

随着步长 $t$ 变大，数据样本 ${\mathbf{x}}_0$ 逐渐失去其可区分的特征。最终当 $T\to \infty$ 时，${\mathbf{x}}_T$ 等价于各向同性高斯分布

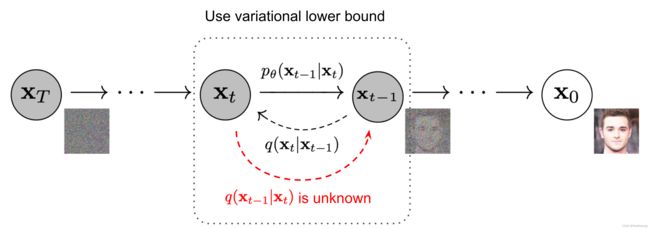
图 2. 通过缓慢添加（去除）噪声生成样本的正向（反向)扩散过程的马尔可夫链。

通过缓慢添加（去除）噪声生成样本的马尔可夫链的正向（反向）扩散过程

上述过程的一个很好的特性是，可以用重新参数化技巧在任何任意时间步长 $t$ 的封闭形式下对 ${\mathbf{x}}_t$ 进行采样

使得 ${\alpha }_t=1-{\beta }_t$ 以及 ${\bar{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$:

$$\begin{array}{rlr}{\mathbf{x}}_t& =\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{z}}_{t-1}& \text{ ;where }{\mathbf{z}}_{t-1},{\mathbf{z}}_{t-2},\cdots \sim \mathcal{N}(0,\mathbf{I})\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\bar{\mathbf{z}}}_{t-2}& \text{ ;where }{\bar{\mathbf{z}}}_{t-2}\text{ merges two Gaussians (*).}\\ & =\dots & \\ & =\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{z}& \\ q({\mathbf{x}}_t|{\mathbf{x}}_0)& =\mathcal{N}({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t)\mathbf{I})& \end{array}$$

(*) **当合并两个具有不同方差的高斯时，$\mathcal{N}(0,{\sigma }_1^2\mathbf{I})$ 和 $\mathcal{N}(0,{\sigma }_2^2\mathbf{I})$，新分布为 $\mathcal{N}(0,({\sigma }_1^2+{\sigma }_2^2)\mathbf{I})$ 。这里合并的标准差是 **
$$\sqrt{(1-{\alpha }_t)+{\alpha }_t(1-{\alpha }_{t-1})}=\sqrt{1-{\alpha }_t{\alpha }_{t-1}}$$

通常，当样本变得更嘈杂时，可以承受更大的更新步长，所以 ${\beta }_1<{\beta }_2<\cdots <{\beta }_T$ 因此 ${\bar{\alpha }}_1>\cdots >{\bar{\alpha }}_T$

Connection with stochastic gradient Langevin dynamics

Langevin dynamics 是物理学中的一个概念，用于对分子系统进行统计建模。结合随机梯度下降，stochastic gradient Langevin dynamics (http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.226.363) 可以仅使用马尔可夫更新链中的梯度 ${\nabla }_{\mathbf{x}}\log p(\mathbf{x})$ 从概率密度 $p(\mathbf{x})$ 生成样本：

$${\mathbf{x}}_t={\mathbf{x}}_{t-1}+\frac{ϵ}{2}{\nabla }_{\mathbf{x}}\log p({\mathbf{x}}_{t-1})+\sqrt{ϵ}{\mathbf{z}}_t,\text{where }{\mathbf{z}}_t\sim \mathcal{N}(0,\mathbf{I})$$

其中 $ϵ$ 为步长，当 $T\to \infty ,ϵ\to 0$ , ${\mathbf{x}}_T$ 等于真实概率密度 $p(\mathbf{x})$。

与标准 SGD 相比，stochastic gradient Langevin dynamics 将高斯噪声注入到参数更新中，以避免陷入局部最小值。

1.2 Reverse diffusion process

如果可以反转上述过程并从 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 中采样，将能够从高斯噪声输入 ${\mathbf{x}}_T\sim \mathcal{N}(0,\mathbf{I})$ 中重新创建真实样本。值得一提的是，如果 ${\beta }_t$ 足够小，$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 也将是高斯分布的。不过估计 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 是不可行的，因为它需要使用整个数据集，因此需要学习一个模型 $p_{\theta }$ 来逼近这些条件概率，以便运行反向扩散过程。

$$p_{\theta }({\mathbf{x}}_{0:T})=p({\mathbf{x}}_T)\prod _{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$$

图 3. 数据建模的扩散模型训练示例。

值得注意的是，当以 ${\mathbf{x}}_0$ 为条件时，反向条件概率是易于处理的：

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_{t-1};\tilde{\mathbf{\mu }}({\mathbf{x}}_t,{\mathbf{x}}_0),{\tilde{\beta }}_t\mathbf{I})$$

使用贝叶斯定理，则有：

$$\begin{array}{rl}q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)& =q({\mathbf{x}}_t|{\mathbf{x}}_{t-1},{\mathbf{x}}_0)\frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{q({\mathbf{x}}_t|{\mathbf{x}}_0)}\\ & \propto \exp (-\frac{1}{2}(\frac{({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}{)}^2}{{\beta }_t}+\frac{({\mathbf{x}}_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t}\left)\right)\\ & =\exp (-\frac{1}{2}(\frac{{\mathbf{x}}_t^2-2\sqrt{{\alpha }_t}{\mathbf{x}}_t{\mathbf{x}}_{t-1}+{\alpha }_t{\mathbf{x}}_{t-1}^2}{{\beta }_t}+\frac{{\mathbf{x}}_{t-1}^2-2\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{\mathbf{x}}_{t-1}+{\bar{\alpha }}_{t-1}{\mathbf{x}}_0^2}{1-{\bar{\alpha }}_{t-1}}-\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t}\left)\right)\\ & =\exp (-\frac{1}{2}((\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}){\mathbf{x}}_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0){\mathbf{x}}_{t-1}+C({\mathbf{x}}_t,{\mathbf{x}}_0)\left)\right)\end{array}$$

其中 $C({\mathbf{x}}_t,{\mathbf{x}}_0)$ 是一些不涉及 ${\mathbf{x}}_{t-1}$ 的函数，省略了细节。按照标准的高斯密度函数，均值和方差可以参数化如下（回顾一下，${\alpha }_t=1-{\beta }_t$ 和 ${\bar{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$):
$$\begin{array}{rl}{\tilde{\beta }}_t& =1/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})=1/(\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})})=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ {\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)& =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})\\ & =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0\end{array}$$

由于不错的属性，可以代表 ${\mathbf{x}}_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\mathbf{z}}_t)$ 并将其代入上式得到：

$$\begin{array}{rl}{\tilde{\mathbf{\mu }}}_t& =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\mathbf{z}}_t)\\ & =\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{z}}_t)\end{array}$$
如图 2 所示，这种设置与 VAE 非常相似，因此可以使用变分下限来优化负对数似然。

variational lower bound 变分下限（也叫 evidence lower bound， ELBO）

为了衡量两个分布 $q(Z)$ 和 $p(Z|X)$ 的相似程度，常用的度量标准是 Kullback-Leibler (KL) 散度。变分推理的 KL 散度为：

$$\begin{array}{rl}KL\left[q(Z)\Vert p(Z|X)\right]& ={\int }_{Z}q(Z)\log \frac{q(Z)}{p(Z|X)}\\ & =-{\int }_{Z}q(Z)\log \frac{p(Z|X)}{q(Z)}\\ & =-\left({\int }_{Z}q(Z)\log \frac{p(X,Z)}{q(Z)}-{\int }_{Z}q(Z)\log p(X)\right)\\ & =-{\int }_{Z}q(Z)\log \frac{p(X,Z)}{q(Z)}+\log p(X){\int }_{Z}q(Z)\\ & =-L+\log p(X)\end{array}$$

其中 $L$ 为上述的变分下限。又由 ${\int }_{Z}q(Z)=1$ 可得：
$$L=\log p(X)-KL\left[q(Z)\Vert p(Z|X)\right]$$
因为 KL 散度总是大于等于 0，可以推导出：
$$L\le \log p(X)$$

$$\begin{array}{rl}-\log p_{\theta }({\mathbf{x}}_0)& \le -\log p_{\theta }({\mathbf{x}}_0)+D_{\text{KL}}(q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)\Vert p_{\theta }({\mathbf{x}}_{1:T}|{\mathbf{x}}_0))\\ & =-\log p_{\theta }({\mathbf{x}}_0)+{\mathbb{E}}_{{\mathbf{x}}_{1:T}\sim q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\left[\log \frac{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{0:T})/p_{\theta }({\mathbf{x}}_0)}\right]\\ & =-\log p_{\theta }({\mathbf{x}}_0)+{\mathbb{E}}_q[\log \frac{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{0:T})}+\log p_{\theta }({\mathbf{x}}_0)]\\ & ={\mathbb{E}}_q\left[\log \frac{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{0:T})}\right]\\ \text{Let }{L}_{\text{VLB}}& ={\mathbb{E}}_{q({\mathbf{x}}_{0:T})}\left[\log \frac{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{0:T})}\right]\ge -{\mathbb{E}}_{q({\mathbf{x}}_0)}\log p_{\theta }({\mathbf{x}}_0)\end{array}$$

使用 Jensen 不等式也很容易得到相同的结果。假设我们想最小化交叉熵作为学习目标，

Jensen 不等式：

过一个下凸函数上任意两点所作割线一定在这两点间的函数图象的上方，即：
$$tf(x_1)+(1-t)f(x_2)\ge f\left(t{x}_1+(1-t)x_2\right),0\le t\le 1.$$
概率论版本

$\mu$ 是个概率测度。函数 $g$ 换作实值随机变量 $X$。在 $\Omega$ 空间上，任何函数相对于概率测度 $\mu$ 的积分就成了期望值。这不等式就说，若 $\phi$ 是任一凸函数，则：
$$\phi (\mathbb{E}(X))\le \mathbb{E}(\phi (X))$$

$$\begin{array}{rl}{L}_{\text{CE}}& =-{\mathbb{E}}_{q({\mathbf{x}}_0)}\log p_{\theta }({\mathbf{x}}_0)\\ & =-{\mathbb{E}}_{q({\mathbf{x}}_0)}\log (\int p_{\theta }({\mathbf{x}}_{0:T})d{\mathbf{x}}_{1:T})\\ & =-{\mathbb{E}}_{q({\mathbf{x}}_0)}\log (\int q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)\frac{p_{\theta }({\mathbf{x}}_{0:T})}{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}d{\mathbf{x}}_{1:T})\\ & =-{\mathbb{E}}_{q({\mathbf{x}}_0)}\log \left({\mathbb{E}}_{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\frac{p_{\theta }({\mathbf{x}}_{0:T})}{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\right)\\ & \le -{\mathbb{E}}_{q({\mathbf{x}}_{0:T})}\log \frac{p_{\theta }({\mathbf{x}}_{0:T})}{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\\ & ={\mathbb{E}}_{q({\mathbf{x}}_{0:T})}\left[\log \frac{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{0:T})}\right]=L_{\text{VLB}}\end{array}$$

为了将方程中的每个项转换为可分析计算的，可以将目标进一步重写为几个 KL 散度和熵项的组合：
$$\begin{array}{rl}{L}_{\text{VLB}}& ={\mathbb{E}}_{q({\mathbf{x}}_{0:T})}\left[\log \frac{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{0:T})}\right]\\ & ={\mathbb{E}}_q\left[\log \frac{{\prod }_{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})}{p_{\theta }({\mathbf{x}}_T){\prod }_{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}\right]\\ & ={\mathbb{E}}_q[-\log p_{\theta }({\mathbf{x}}_T)+\sum _{t=1}^T\log \frac{q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})}{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}]\\ & ={\mathbb{E}}_q[-\log p_{\theta }({\mathbf{x}}_T)+\sum _{t=2}^T\log \frac{q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})}{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}+\log \frac{q({\mathbf{x}}_1|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}]\\ & ={\mathbb{E}}_q[-\log p_{\theta }({\mathbf{x}}_T)+\sum _{t=2}^T\log (\frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}\cdot \frac{q({\mathbf{x}}_t|{\mathbf{x}}_0)}{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)})+\log \frac{q({\mathbf{x}}_1|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}]\\ & ={\mathbb{E}}_q[-\log p_{\theta }({\mathbf{x}}_T)+\sum _{t=2}^T\log \frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}+\sum _{t=2}^T\log \frac{q({\mathbf{x}}_t|{\mathbf{x}}_0)}{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}+\log \frac{q({\mathbf{x}}_1|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}]\\ & ={\mathbb{E}}_q[-\log p_{\theta }({\mathbf{x}}_T)+\sum _{t=2}^T\log \frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}+\log \frac{q({\mathbf{x}}_T|{\mathbf{x}}_0)}{q({\mathbf{x}}_1|{\mathbf{x}}_0)}+\log \frac{q({\mathbf{x}}_1|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}]\\ & ={\mathbb{E}}_q[\log \frac{q({\mathbf{x}}_T|{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_T)}+\sum _{t=2}^T\log \frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)}{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}-\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)]\\ & ={\mathbb{E}}_q[\underset{L_T}{D_{\text{KL}}(q({\mathbf{x}}_T|{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_T))}+\sum _{t=2}^T\underset{L_{t-1}}{D_{\text{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t))}\underset{L_0}{-\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}]\end{array}$$
分别标记变分下界损失中的每个分量：
$$\begin{array}{rl}{L}_{\text{VLB}}& =L_T+L_{T-1}+\cdots +L_0\\ \text{where }{L}_T& =D_{\text{KL}}(q({\mathbf{x}}_T|{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_T))\\ L_t& =D_{\text{KL}}(q({\mathbf{x}}_t|{\mathbf{x}}_{t+1},{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_t|{\mathbf{x}}_{t+1}))\text{ for }1\le t\le T-1\\ L_0& =-\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)\end{array}$$
$L_{VLB}$ 中的每个 KL 项（$L_0$ 除外）比较两个高斯分布，因此可以以封闭形式计算它们。 $L_T$ 是常数，在训练期间可以忽略，因为 $q$ 没有可学习的参数，而 $x_T$ 是高斯噪声。 $L_0$ 使用从 $\mathcal{N}(x_0;{\mu }_{\theta }(x_1,1),{\Sigma }_{\theta }(x_1,1))$ 派生的单独离散解码器。

1.3 Parameterization of $L_t$ for Training Loss

我们需要学习一个神经网络来逼近反向扩散过程中的条件概率分布 $p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$ ，通过训练 ${\mu }_{\theta }$ 来预测 ${\tilde{\mathbf{\mu }}}_t=\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{z}}_t)$ 。因为 $x_t$ 在训练时可用作输入，可以重新参数化高斯噪声项，以使其在时间步 $t$ 从输入 $x_t$ 预测 $z_t$：
$$\begin{array}{rl}{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t)& =\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{z}}_{\theta }({\mathbf{x}}_t,t))\\ \text{Thus }{\mathbf{x}}_{t-1}& =\mathcal{N}({\mathbf{x}}_{t-1};\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{z}}_{\theta }({\mathbf{x}}_t,t)),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))\end{array}$$
损失项 $L_t$ 被参数化以最小化与 $\tilde{\mathbf{\mu }}$
$$\begin{array}{rl}{L}_t& ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{z}}[\frac{1}{2\Vert {\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t){\Vert }_2^2}\Vert {\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)-{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t){\Vert }^2]\\ & ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{z}}[\frac{1}{2\Vert {\mathbf{\Sigma }}_{\theta }{\Vert }_2^2}\Vert \frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{z}}_t)-\frac{1}{\sqrt{{\alpha }_t}}({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{z}}_{\theta }({\mathbf{x}}_t,t)\left){\Vert }^2\right]\\ & ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{z}}[\frac{{\beta }_t^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)\Vert {\mathbf{\Sigma }}_{\theta }{\Vert }_2^2}\Vert {\mathbf{z}}_t-{\mathbf{z}}_{\theta }({\mathbf{x}}_t,t){\Vert }^2]\\ & ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{z}}[\frac{{\beta }_t^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)\Vert {\mathbf{\Sigma }}_{\theta }{\Vert }_2^2}\Vert {\mathbf{z}}_t-{\mathbf{z}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\mathbf{z}}_t,t){\Vert }^2]\end{array}$$

Simplification

在忽略加权项的简化目标下，训练扩散模型效果更好：
$$L_t^{\text{simple}}={\mathbb{E}}_{{\mathbf{x}}_0,{\mathbf{z}}_t}[\Vert {\mathbf{z}}_t-{\mathbf{z}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\mathbf{z}}_t,t){\Vert }^2]$$
最后一个简单的目标是：
$$L_{\text{simple}}=L_t^{\text{simple}}+C$$
其中 $C$ 是一个不依赖于 $\theta$ 的常数。

图 4 DDPM 中的训练和采样算法

参考资料

• What are Diffusion Models? | Lil’Log (lilianweng.github.io)
• Understanding the Variational Lower Bound (xyang35.github.io)
• [2006.11239] Denoising Diffusion Probabilistic Models (arxiv.org)