CVPR2020 MOT MPNTracker 论文解读
MPNTracker——Learning a Neural Solver for Multiple Object Tracking
-
- 摘要
- 1. 前言
- 2. 基于图的跟踪问题
-
- 2.1 问题定义
- 2.2 网络流定义
- 2.3 图学习方法
- 3. 基于消息传递机制的跟踪(Message Passing Networks, MPN)
-
- 3.1 消息传递网络
- 3.2 时间感知的消息传递
- 3.3 特征编码
-
- 3.3.1 外观特征嵌入
- 3.3.2 几何信息嵌入
- 3.4 训练及推理
-
- 3.4.1 训练损失
- 3.4.2 推理
- 4. 网络结构
-
- 4.1 特征编码
-
- 4.1.1 外观特征提取网络 N v e n c N_v^{enc} Nvenc
- 4.1.2 几何特征提取网络 N e e n c N_e^{enc} Neenc
- 4.2 消息传递网络
-
- 4.2.1 边更新网络 N e N_e Ne
- 4.2.2 过去节点特征融合网络 N v p a s t N_v^{past} Nvpast
- 4.2.3 未来节点特征融合网络 N v f u t N_v^{fut} Nvfut
- 4.2.4 节点更新网络 N v N_v Nv
- 4.3 边分类网络 N e c l a s s N_e^{class} Neclass
论文链接: Learning a Neural Solver for Multiple Object Tracking CVPR2020
论文代码:https://github.com/dvl-tum/mot_neural_solver
摘要
Abstract: Graphs offer a natural way to formulate Multiple Object Tracking (MOT) within the tracking-by-detection paradigm. However, they also introduce a major challenge for learning methods, as defining a model that can operate on such structured domain is not trivial. As a consequence, most learning-based work has been devoted to learning better features for MOT, and then using these with wellestablished optimization frameworks. In this work, we exploit the classical network flow formulation of MOT to define a fully differentiable framework based on Message Passing Networks (MPNs). By operating directly on the graph domain, our method can reason globally over an entire set of detections and predict final solutions. Hence, we show that learning in MOT does not need to be restricted to feature extraction, but it can also be applied to the data association step. We show a significant improvement in both MOTA and IDF1 on three publicly available benchmarks.
Our code is available at https://bit.ly/motsolv.
摘要:图提供了一种自然的方法,可以在检测跟踪范式中描述多目标跟踪(MOT)。然而,它们也给学习方法带来了一个重大挑战,因为定义一个能够在这种结构化领域中运行的模型并非易事。因此,大多数基于学习的工作都致力于为MOT学习更好的功能,然后将其与完善的优化框架结合使用。在这项工作中,我们利用MOT的经典网络流公式来定义一个基于消息传递网络(MPN)的完全可微框架。通过直接在图域上操作,我们的方法可以对整个检测集进行全局推理,并预测最终解。因此,我们证明了MOT中的学习不需要局限于特征提取,它也可以应用于数据关联步骤。我们展示了MOTA和IDF1在三个公开的基准上的显著改进。
1. 前言
我们建议将这两项任务结合到一个统一的基于学习的解算器中,该解算器可以:(i)学习MOT的功能,以及(ii)学习通过对整个图形进行推理来提供解决方案。为此,我们利用MOT[87]的经典网络流公式来定义我们的模型。我们的方法不是学习成对成本,然后在可用的解算器中使用这些成本,而是学习直接预测图的最终轨迹划分。为此,我们通过消息传递网络(MPN)直接在自然MOT域(即图形域)中执行学习。我们的MPN学习将深度特征结合到整个图形的高阶信息中。因此,尽管依赖于一个简单的图形公式,我们的方法仍然能够解释检测之间的全局交互。我们展示了我们的框架相对于最先进的技术有了实质性的改进,不需要大量设计的功能,并且比一些传统的图划分方法快一个数量级。
总之,我们做出以下贡献:
•我们提出了一种基于消息传递网络的MOT求解器,它可以利用问题的自然图形结构来执行特征学习和最终解决方案预测。
•受MOT经典图公式的启发,我们提出了一种新的时间感知神经消息传递更新步骤。
2. 基于图的跟踪问题
我们的方法基于MOT的经典最小成本流观点。为了提供一些背景知识并正式介绍我们的方法,我们首先对网络流MOT公式进行概述。然后,我们将解释如何利用这个框架将数据关联任务重新表述为一个学习问题。
2.1 问题定义
基于检测的跟踪中,我们会获得检测集合 O = { o 1 , . . . , o n } O=\{o_1,...,o_n\} O={o1,...,on}作为输入, n n n表示所有帧中的所有检测总数。每个检测出的目标 o i = ( a i , p i , t i ) o_i=(a_i,p_i,t_i) oi=(ai,pi,ti), a i a_i ai表示bbox中的原始像素, p i p_i pi表示其坐标, t i t_i ti表示其时间戳即第 i i i帧。一段轨迹定义为时间序列上的检测结果 T i = { o i 1 , . . . , o i n i } T_i=\{o_{i_1},...,o_{i_{n_i}}\} Ti={oi1,...,oini}, n i n_i ni表示第 i i i个轨迹的检测数量有n个。MOT的目标是找出所有的轨迹 T ∗ = { T 1 , . . . , T m } T_{*}=\{T_1,...,T_m\} T∗={T1,...,Tm}和最佳的检测结果 O O O。
此跟踪问题可以被建模为无向图 G = ( V , E ) G=(V,E) G=(V,E),其中 V : = { 1 , . . . , n } V:=\{1,...,n\} V:={1,...,n}, E = e d g e E=edge E=edge。每个节点 i ∈ V i\in{V} i∈V代表一个独立的检测结果 o i ∈ O o_i\in{O} oi∈O。构造边集合 E E E,以便连接不同帧中的每对检测,即节点,从而允许恢复丢失检测的轨迹(不同帧之间的节点会连接,而同一帧中的节点不会相连)。现在,将原始检测结果集合划分轨迹的任务可以看作是将图中的节点分组为断开连接的组件,即图的边预测(link prediction)。因此,每段轨迹 T i = { o i 1 , . . . , o i n i } T_i=\{o_{i_1},...,o_{i_{n_i}}\} Ti={oi1,...,oini}在场景中能被映射到一组连接的节点中。
2.2 网络流定义
为了表示图划分,我们为图中的每条边引入了一个二进制变量。在经典的最小成本流公式中,若(i)属于同一轨迹,(ii)在轨迹内是暂时连续的;那么其边的标签被定义为1,所有剩余的边都为0。
一段轨迹 T i = { o i 1 , . . . , o i n i } T_i=\{o_{i_1},...,o_{i_{n_i}}\} Ti={oi1,...,oini}由一组边等价地表示, { ( i 1 , i 2 ) , . . . , ( i n i − 1 , i n i } ⊂ E \{(i_1,i_2),...,(i_{n_i-1}, i_{n_i}\}\subset{E} {(i1,i2),...,(ini−1,ini}⊂E,对应于其在图中的时间顺序路径。我们将使用这个来定义边标签。对于不同时间戳 ( i , j ) ∈ E (i,j)\in{E} (i,j)∈E中的每对节点,我们将二进制变量 y ( i , j ) y_{(i,j)} y(i,j)定义为:
y ( i , j ) = { 1 ∃ T k ∈ T ∗ s . t . ( i , j ) ∈ T k 0 o t h e r w i s e y_{(i,j)}= \begin{cases} 1 & & \exists{T_k\in{T_{*}s.t.(i,j)\in{T_k}}}\\ 0 & & otherwise \end{cases} y(i,j)={10∃Tk∈T∗s.t.(i,j)∈Tkotherwise
当 y ( i , j ) = 1 y_{(i,j)}=1 y(i,j)=1时边 ( i , j ) (i,j) (i,j)激活。我们假设轨迹 T T T是节点不相交的,即一个节点不能在多个轨迹段中存在。因此, y ^ \hat{y} y^必须满足线性约束,对于每个节点 i ∈ V i\in{V} i∈V:
∑ ( j , i ) ∈ E s . t . t j < t i y ( j , i ) ≤ 1 ∑ ( i , k ) ∈ E s . t . t i < t k y ( i , k ) ≤ 1 \sum_{(j,i)\in{E}\;s.t.\;t_j
即对于当前节点 i i i,不能连多个之前的节点 j j j,不能连多个之后的节点 k k k。上述不等式是流守恒约束的简化形式。在我们的设置中,它们强制每个节点通过激活边链接到过去帧中最多一个节点和未来帧中最多一个节点。
2.3 图学习方法
为了使用我们定义的框架获得图划分,标准方法是首先将代价 c ( i , j ) c_{(i,j)} c(i,j)与每个二元变量 y ( i , j ) y_{(i,j)} y(i,j)相关联。该代价编码了边处于激活状态的可能性。通过优化找到最终分区:
m i n y ∑ ( i , j ) ∈ E c ( i , j ) y ( i , j ) s . t . ∑ ( j , i ) ∈ E s . t . t j < t i y ( j , i ) ≤ 1 ∑ ( i , k ) ∈ E s . t . t i < t k y ( i , k ) ≤ 1 y ( i , j ) ∈ { 0 , 1 } , ( i , j ) ∈ E \begin{aligned} min_y\quad & {\sum_{(i,j)\in{E}}}c_{(i,j)y_{(i,j)}}\\ s.t.\quad & \sum_{(j,i)\in{E}\;s.t.\;t_j
可以用可用解算器在多项式时间内求解。
相反,我们建议直接学习预测图中哪些边将是激活的,即预测二元变量 y y y的最终值。为此,我们将任务视为边上的分类问题(link prediction),其中我们的标签是二元变量 y y y。总体而言,我们利用我们刚刚提出的经典网络流公式,将MOT问题视为完全可学习的任务。
3. 基于消息传递机制的跟踪(Message Passing Networks, MPN)
我们的主要贡献是基于我们在前一节中描述的图公式,建立一个可微框架,将多目标跟踪器训练为边分类器。给定一组输入的检测结果,我们的模型经过训练,可以预测图中每条边的二元流变量y的值。我们的方法基于一种与众不同的消息传递网络(MPN),能够捕捉MOT问题的图结构。在我们提出的MPN框架内,外观和几何线索在整个检测集合中传播,使我们的模型能够对整个图进行全局推理。
我们的方法主要由四个主要阶段组成:
- 构造图:给定一个视频的检测结果集合,我们构建图,其中节点对应于检测,边对应于节点之间的连接。
- 特征编码:我们从bbox中的行人图像利用卷积神经网络(CNN)提取外观特征嵌入(ReID操作)初始化节点。对于每一条边,也就是说,对于不同帧中的每一对检测,我们计算一个向量,其中的特征编码是其边界框的相对大小、位置和时间距离。然后我们将其反馈给多层感知器(MLP),该感知器返回一个几何嵌入。即
- 节点编码:目标的外观特征
- 边编码:目标间的大小、位置和时间距离作为输入,MLP的输出作为两个节点间的边编码。
- 消息传递:我们在图上执行一系列消息传递步骤。直观地说,对于每一轮消息传递,节点分享外观信息给边,而边分享几何信息给节点。这将生成包含高阶信息的节点和边的更新嵌入,这些信息取决于整个图结构。
- 节点的外观特征分享给边用于边信息更新
- 边的距离信息分享给节点用于节点信息更新
- 训练:我们使用最终的边嵌入对激活/非激活的边二分类,并使用交叉熵损失函数进行训练(cross-entropy loss)。测试阶段,我们的模型预测每条边的结果为0到1的连续近似值作为目标流变量。然后,我们按照一个简单的方案对它们进行取整,并获得最终的轨迹。如图1所示。
- 我们接收一组帧和检测结果作为输入
- 我们构造了一个图,其中节点表示检测结果,不同帧上的所有节点都通过边连接
- 我们用CNN初始化图中的节点嵌入,用MLP编码几何信息初始化边嵌入(图中未显示)。这些嵌入中包含的信息通过消息传递在图中传播固定次数的迭代
- 一旦该过程终止,神经信息传递产生的嵌入将用于将边分为激活(绿色)和非激活(红色)。在训练期间,我们计算预测的交叉熵损失预测的边连接与真值(真实的边连接)
- 在推理时,我们遵循一个简单的取整方案对分类分数进行二值化,并获得最终的轨迹。
3.1 消息传递网络
这一节我们简单介绍MPN的机制。
| symbol | meaning |
|---|---|
| G = ( V , E ) G=(V,E) G=(V,E) | 图 G G G由节点 V V V和边 E E E构成 |
| h i ( 0 ) i ∈ V h_i^{(0)}\quad i\in{V} hi(0)i∈V | 节点 i i i的嵌入(特征向量) |
| h ( i , j ) ( 0 ) ( i , j ) ∈ E h_{(i,j)}^{(0)}\quad (i,j)\in E h(i,j)(0)(i,j)∈E | 边 i i i的嵌入(特征向量) |
| ( v → e ) (v\rightarrow e) (v→e) | 节点到边的更新 |
| ( e → v ) (e\rightarrow v) (e→v) | 边到节点的更新 |
| N e N_e Ne | 更新边嵌入的可学习函数,输入为边两头节点的特征和自身特征 |
| N v N_v Nv | 更新节点嵌入的可学习函数,输入为此节点之前的嵌入和更新后的边嵌入 |
| N i ⊂ V N_i\subset V Ni⊂V | 当前节点 i i i的邻居节点,是节点集合V的子集, |
| [ . ] [.] [.] | 拼接操作,concat |
| Φ ( ) \Phi() Φ() | 聚合函数,一般为 m a x max max, m e a n mean mean, s u m sum sum |
MPN的目标是学习一个函数,将包含在节点和边特征向量中的信息在 G G G上传播。
消息传递步骤是更新边和节点的嵌入,最终的目的是更新节点特征并做边预测。每次消息传递依次分为两个步骤更新:
- 节点到边的更新 ( v → e ) (v\rightarrow e) (v→e)
- 边到节点的更新 ( e → v ) (e\rightarrow v) (e→v)
更新按固定的迭代次数 L L L顺序执行。对于每个 l ∈ { 1 , . . . , L } l\in \{ 1,...,L\} l∈{1,...,L},更新的一般形式如下:
( v → e ) h ( i , j ) ( l ) = N e ( [ h i ( l − 1 ) , h j ( l − 1 ) , h ( i , j ) ( l − 1 ) ] ) ( e → v ) m ( i , j ) ( l ) = N v ( [ h i ( l − 1 ) , h ( i , j ) ( l ) ] ) h i ( l ) = Φ ( { m ( i , j ) ( l ) } j ∈ N i ) \begin{aligned} (v\rightarrow e)\quad h_{(i,j)}^{(l)} &= N_e([h_i^{(l-1)},\, h_j^{(l-1)},\, h_{(i,j)}^{(l-1)}])\\ (e\rightarrow v)\quad m_{(i,j)}^{(l)} &= N_v([h_i^{(l-1)},\, h_{(i,j)}^{(l)}])\\ h_i^{(l)} &= \Phi(\{m_{(i,j)}^{(l)} \}_{j\in N_i}) \end{aligned} (v→e)h(i,j)(l)(e→v)m(i,j)(l)hi(l)=Ne([hi(l−1),hj(l−1),h(i,j)(l−1)])=Nv([hi(l−1),h(i,j)(l)])=Φ({m(i,j)(l)}j∈Ni)
公式对比:
通用消息传递神经网络的数学表达
h i ( l ) = γ ( l ) ( h i ( l − 1 ) , Φ j ∈ N i { M ( l ) } ) {h_i^{(l)}}=\gamma^{(l)}(h_i^{(l-1)}, \Phi_{j\in N_i}\{ M^{(l)}\}) hi(l)=γ(l)(hi(l−1),Φj∈Ni{M(l)})
此消息传递神经网络的数学表达
h i ( l ) = Φ j ∈ N i { M ( l ) } {h_i^{(l)}} = \Phi_{j\in N_i}\{ M^{(l)}\} hi(l)=Φj∈Ni{M(l)}其中
M ( l ) M^{(l)} M(l)称为message——当前节点从周围多个节点或边拿过来的消息(嵌入、特征向量、知识)。
M ( l ) ( h i ( l − 1 ) , h j ( l − 1 ) , e ( i , j ) ) = N v ( [ h i ( l − 1 ) , N e ( [ h i ( l − 1 ) , h j ( l − 1 ) , h ( i , j ) ( l − 1 ) ] ) ] ) M^{(l)}(h_i^{(l-1)},h_j^{(l-1)},e_{(i,j)}) = N_v([h_i^{(l-1)},\, N_e([h_i^{(l-1)},\, h_j^{(l-1)},\, h_{(i,j)}^{(l-1)}])]) M(l)(hi(l−1),hj(l−1),e(i,j))=Nv([hi(l−1),Ne([hi(l−1),hj(l−1),h(i,j)(l−1)])])
Φ j ∈ N i \Phi_{j\in N_i} Φj∈Ni称为aggregation——当前节点拿过来的很多消息通过什么方式融合、相加融合>(sum),平均融合(mean),最大融合(max)
Φ j ∈ N i = ∑ j ∈ N i \Phi_{j\in N_i} = \sum_{j\in N_i} Φj∈Ni=j∈Ni∑
γ ( l ) \gamma^{(l)} γ(l)称为update——当前节点得到消息后,与自身的信息整合更新。但一般在message>阶段就会加入自身信息,所以update很少有人用。
γ ( l ) = N o n e \gamma^{(l)} = None γ(l)=None
在L次迭代之后,每个节点都包含图中距离L处所有其他节点的信息。因此,L扮演着与CNN感受野类似的角色,允许嵌入捕获上下文信息。
3.2 时间感知的消息传递
之前的消息传递框架设计用于处理任意图。然而MOT的图有一个非常特殊的结构。我们需要基于MOT的图结构对消息传递做改进,即加入时间感知。
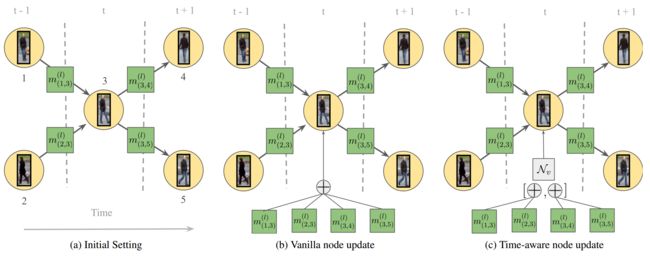
箭头指向时间方向,为第t-1帧,第t帧,第t+1帧。在此图中,有 N 3 p a s t = { 1 , 2 } N_3^{past}=\{1,2\} N3past={1,2}, N 3 f u t = { 4 , 5 } N_3^{fut}=\{4,5\} N3fut={4,5}。a展示了节点3执行message的情况。b展示了普通的aggregation操作,即所有邻居的嵌入被一起聚合。c展示了我们提出的更新,其中来自过去和未来帧的嵌入分别聚合(aggregation),然后concat并输入到MLP中,以获取新的节点嵌入。
回想一下边到节点的更新,它允许每个节点与其邻居进行比较,并聚合邻居节点的信息,以使用进一步的上下文更新其嵌入。流守恒约束的结构意味着每个节点最多可以连接到未来帧中的一个节点和过去帧中的另一个节点。可以说,一次聚合所有相邻嵌入会使更新的节点嵌入难以捕获这些约束是否被违反(有关约束满足度分析,请参见第5.2节)。
更通常地讲,将MOT图的时间结构显式地编码到MPN公式中对于我们的学习任务来说是一个有用的先验知识。为了实现这一目标,我们通过将聚合分解为两部分,将边到节点的更新修改为时间感知更新规则:一部分在过去的节点上,另一部分在未来的节点上。形式上,让我们分别用 N i f u t N_i^{fut} Nifut和 N i p a s t N_i^{past} Nipast来表示未来帧和过去帧中 i i i的相邻节点。让我们也定义两个不同的MLP,即 N v f u t N_v^{fut} Nvfut和 N v p a s t N_v^{past} Nvpast。在每个消息传递步骤 l l l和每个节点 i ∈ V i\in V i∈V中,我们首先计算其所有邻居 j ∈ N i j\in N_i j∈Ni的过去和未来边到节点嵌入,如下所示:
m ( i , j ) ( l ) = { N v p a s t ( [ h i ( l − 1 ) , h ( i , j ) ( l ) , h ( i ) ( 0 ) ] ) i f j ∈ N i p a s t N v f u t ( [ h i ( l − 1 ) , h ( i , j ) ( l ) , h ( i ) ( 0 ) ] ) i f j ∈ N i f u t m_{(i,j)}^{(l)}= \begin{cases} N_v^{past}([h_i^{(l-1)}, h_{(i,j)}^{(l)}, h_{(i)}^{(0)}])\quad\quad if \quad\quad j\in N_i^{past}\\ N_v^{fut}([h_i^{(l-1)}, h_{(i,j)}^{(l)}, h_{(i)}^{(0)}])\quad\quad if \quad\quad j\in N_i^{fut} \end{cases} m(i,j)(l)={Nvpast([hi(l−1),h(i,j)(l),h(i)(0)])ifj∈NipastNvfut([hi(l−1),h(i,j)(l),h(i)(0)])ifj∈Nifut
注意,初始的特征嵌入 h ( i ) ( 0 ) h_{(i)}^{(0)} h(i)(0)被加入计算,并分别聚合past和future的特征,这取决于邻居节点 i i i是否在未来或过去的位置上:
h i , p a s t ( l ) = ∑ j ∈ N i p a s t m ( i , j ) ( l ) h i , f u t ( l ) = ∑ j ∈ N i f u t m ( i , j ) ( l ) h i ( l ) = N v ( [ h i , p a s t ( l ) , h i , f u t ( l ) ] ) \begin{aligned} h_{i,past}^{(l)} &= \sum_{j\in N_i^{past}}m_{(i,j)}^{(l)}\\ h_{i,fut}^{(l)} &= \sum_{j\in N_i^{fut}}m_{(i,j)}^{(l)} \\ h_i^{(l)} &= N_v([h_{i,past}^{(l)}, h_{i,fut}^{(l)}]) \end{aligned} hi,past(l)hi,fut(l)hi(l)=j∈Nipast∑m(i,j)(l)=j∈Nifut∑m(i,j)(l)=Nv([hi,past(l),hi,fut(l)])
3.3 特征编码
作为构造图的节点和边的特征,特征如下:
3.3.1 外观特征嵌入
采用卷积神经网络(CNN),网络用 N v e n c N_v^{enc} Nvenc表示。从裁切出的人的RGB数据中 a a a学习人物外观特征。其实就是最普通的ReID任务,对所有检测结果提取目标特征,得到初始的节点嵌入 h i ( 0 ) h_{i}^{(0)} hi(0)。
3.3.2 几何信息嵌入
采用多层感知机(MLP),网络用 N e e n c N_e^{enc} Neenc表示。对于相连的两个节点,即不同帧的两个检测结果,在图像中的bbox位置、大小、以及时间间隔都有一定的差异,为了获取这种差异,需要将这些信息作为输入进行学习,输出作为边嵌入。
对于两个检测结果 ( x i , y i , h i , w i ) {(x_i,y_i,h_i,w_i)} (xi,yi,hi,wi)和 ( x j , y j , h j , w j ) {(x_j,y_j,h_j,w_j)} (xj,yj,hj,wj),我们计算它们的相对距离和大小为,并加入时间信息(所在帧帧数)、外观相似度信息(外观特征的L2距离)为:
( 2 ( x j − x i ) h i + h j , 2 ( y j − y i ) h i + h j , l o g h i h j , l o g w i w j , t j − t i , ∣ ∣ N v e n c ( a j ) − N e e n c ( a i ) ∣ ∣ 2 ) {(\cfrac{2(x_j-x_i)}{h_i+h_j},\quad \cfrac{2(y_j-y_i)}{h_i+h_j},\quad log{\cfrac{h_i}{h_j}},\quad log{\cfrac{w_i}{w_j}},\quad t_j-t_i,\quad ||N_v^{enc}(a_j)-N_e^{enc}(a_i)||_2)} (hi+hj2(xj−xi),hi+hj2(yj−yi),loghjhi,logwjwi,tj−ti,∣∣Nvenc(aj)−Neenc(ai)∣∣2)
然后将这个参数送进 N e e n c N_e^{enc} Neenc中,得到初始的边嵌入 h ( i , j ) ( 0 ) h_{(i,j)}^{(0)} h(i,j)(0)。
3.4 训练及推理
3.4.1 训练损失
为了分类边,我们使用MLP和sigmoid单输出,网络用 N e c l a s s N_e^{class} Neclass表示。对于每条边 ( i , j ) ∈ E (i,j)\in E (i,j)∈E,通过MPN的输出嵌入 h ( i , j ) ( l ) h_{(i,j)}^{(l)} h(i,j)(l)送入 N e c l a s s N_e^{class} Neclass,计算其预测结果 y ^ ( i , j ) ( l ) \hat{y}_{(i,j)}^{(l)} y^(i,j)(l)。为了训练,我们在最后一次消息传递更新后,使用二值交叉熵损失(BCE loss)训练网络,损失函数如下:
L = − 1 ∣ E ∣ ∑ l = l 0 l = L ∑ ( i , j ) ∈ E w ⋅ y ( i , j ) l o g ( y ^ ( i , j ) ( l ) ) + ( 1 − y ( i , j ) ) l o g ( 1 − y ^ ( i , j ) ( l ) ) L=\frac{-1}{|E|}\sum_{l=l_0}^{l=L}\sum_{(i,j)\in E}w \cdot y_{(i,j)}log(\hat{y}_{(i,j)}^{(l)})+(1-y_{(i,j)})log(1-\hat{y}_{(i,j)}^{(l)}) L=∣E∣−1l=l0∑l=L(i,j)∈E∑w⋅y(i,j)log(y^(i,j)(l))+(1−y(i,j))log(1−y^(i,j)(l))
其中 l 0 ∈ { 1 , . . . , L } l_0\in \{ 1,...,L \} l0∈{1,...,L}表示第一次到最后一次消息传递步骤,即每一次传递都计算进loss中。 w w w表示用于为1值标签加权,以解释激活边和非激活边之间的高度不平衡。(在多目标跟踪中,非激活边只会更多)
3.4.2 推理
在推理过程中,我们将在最后一个消息传递步骤从模型中获得的一组输出值解释为我们的MOT问题的解决方案,即变量y的最终值。由于这些预测是sigmoid单位的输出,它们的值介于0和1之间。获得硬0或1决策的一种简单方法是通过阈值化对输出进行二值化。然而,该程序通常不能保证流守恒约束。在实践中,由于提出了时间感知更新步骤,当阈值为0.5时,我们的方法将平均满足98%以上的约束。之后,一个简单的贪婪舍入方案就足以获得一个可行的二进制输出。通过简单的线性规划,也可以有效地获得精确的最优舍入解。我们在附录B中解释了这两种程序。
加入贪婪匹配或线性规划原因是,网络的输出不能保证满足每个节点前后至多各连接一个节点,需要进一步匹配。
4. 网络结构
4.1 特征编码
4.1.1 外观特征提取网络 N v e n c N_v^{enc} Nvenc
| layer number | Type | Output Size |
|---|---|---|
| 0 Image Patch | Input | [ 3 , 128 , 64 ] [3, 128, 64] [3,128,64] |
| 1 | conv 7 × 7 7 \times 7 7×7 | [ 64 , 64 , 32 ] [64, 64, 32] [64,64,32] |
| 2 | max pool 3 × 3 3\times 3 3×3 | [ 64 , 32 , 16 ] [64, 32, 16] [64,32,16] |
| 3 | conv1 | [ 256 , 32 , 16 ] [256, 32, 16] [256,32,16] |
| 4 | conv2 | [ 512 , 16 , 8 ] [512, 16, 8] [512,16,8] |
| 5 | conv3 | [ 1024 , 8 , 4 ] [1024, 8, 4] [1024,8,4] |
| 6 | conv4 | [ 2048 , 8 , 4 ] [2048, 8, 4] [2048,8,4] |
| 7 | GAP | 2048 |
| 8 | FC+ReLU | 512 |
| 9 | FC+ReLU | 128 |
| 10 h i ( 0 ) h_{i}^{(0)} hi(0) | FC+ReLU | 32 |
4.1.2 几何特征提取网络 N e e n c N_e^{enc} Neenc
| layer number | Type | Output Size |
|---|---|---|
| 0 [ P o s i t i o n , T i m e , S i m i l a r i t y ] [Position,Time,Similarity] [Position,Time,Similarity] | Input | 6 |
| 1 | FC+ReLU | 18 |
| 2 | FC+ReLU | 18 |
| 3 h ( i , j ) ( 0 ) h_{(i,j)}^{(0)} h(i,j)(0) | FC+ReLU | 16 |
4.2 消息传递网络
4.2.1 边更新网络 N e N_e Ne
| layer number | Type | Output Size |
|---|---|---|
| 0 [ h i ( l − 1 ) , h j ( l − 1 ) , h ( i , j ) ( l − 1 ) ] [h_i^{(l-1)},\, h_j^{(l-1)},\, h_{(i,j)}^{(l-1)}] [hi(l−1),hj(l−1),h(i,j)(l−1)] | Input | 160 |
| 1 | FC+ReLU | 80 |
| 2 h ( i , j ) ( l ) h_{(i,j)}^{(l)} h(i,j)(l) | FC+ReLU | 16 |
注:由于在边特征更新中,图的整体结构不会改变。作者在代码中设置了两种不同的输入,即加入初始节点特征与否、加入初始边特征与否。
因此此网络在超参设置下可以有最少80的输入,为:
[ h i ( l − 1 ) , h j ( l − 1 ) , h ( i , j ) ( l − 1 ) ] [h_i^{(l-1)},\, h_j^{(l-1)},\, h_{(i,j)}^{(l-1)}] [hi(l−1),hj(l−1),h(i,j)(l−1)]
最多可以有160的输入,为:
[ h i ( 0 ) , h j ( 0 ) , h ( i , j ) ( 0 ) , h i ( l − 1 ) , h j ( l − 1 ) , h ( i , j ) ( l − 1 ) ] [h_i^{(0)},\, h_j^{(0)},\, h_{(i,j)}^{(0)}, \, h_i^{(l-1)},\, h_j^{(l-1)},\, h_{(i,j)}^{(l-1)}] [hi(0),hj(0),h(i,j)(0),hi(l−1),hj(l−1),h(i,j)(l−1)]
4.2.2 过去节点特征融合网络 N v p a s t N_v^{past} Nvpast
| layer number | Type | Output Size |
|---|---|---|
| 0 [ h i ( 0 ) , h i ( l − 1 ) , h ( i , j ) ( l ) ] [h_{i}^{(0)},h_{i}^{(l-1)},h_{(i,j)}^{(l)}] [hi(0),hi(l−1),h(i,j)(l)] | Input | 80 |
| 1 | FC+ReLU | 56 |
| 2 h i , p a s t ( l ) h_{i,past}^{(l)} hi,past(l) | FC+ReLU | 32 |
4.2.3 未来节点特征融合网络 N v f u t N_v^{fut} Nvfut
| layer number | Type | Output Size |
|---|---|---|
| 0 [ h i ( 0 ) , h i ( l − 1 ) , h ( i , j ) ( l ) ] [h_{i}^{(0)},h_{i}^{(l-1)},h_{(i,j)}^{(l)}] [hi(0),hi(l−1),h(i,j)(l)] | Input | 80 |
| 1 | FC+ReLU | 56 |
| 2 h i , f u t ( l ) h_{i,fut}^{(l)} hi,fut(l) | FC+ReLU | 32 |
4.2.4 节点更新网络 N v N_v Nv
| layer number | Type | Output Size |
|---|---|---|
| 0 [ h i , p a s t ( l ) , h i , f u t ( l ) ] [h_{i,past}^{(l)}, h_{i,fut}^{(l)}] [hi,past(l),hi,fut(l)] | Input | 64 |
| 1 h i ( l ) h_{i}^{(l)} hi(l) | FC+ReLU | 32 |
4.3 边分类网络 N e c l a s s N_e^{class} Neclass
| layer number | Type | Output Size |
|---|---|---|
| 0 h ( i , j ) ( l ) h_{(i,j)}^{(l)} h(i,j)(l) | Input | 16 |
| 1 | FC+ReLU | 8 |
| 2 p r e d i c t i o n ∈ [ 0 , 1 ] prediction\in [0,1] prediction∈[0,1] | FC+Sigmoid | 1 |