深度学习入门初探——感知机的初级理解

        感知机是由一名美国学者在1957年提出来的，作为神经网络和深度学习的起源算法，学习感知机的构造也是学习通向神经网络和深度学习的一种重要思想。

        感知机可以有一个或者多个输入信号，输出一个信号。每个输入信号都有各自的权重，这些权重发挥着控制各个信号重要性的作用，也就是说权重越大，对应该权重的信号的重要性就越高。下面我们以两输入的感知机来描述一下真值表的逻辑，先看一下两个式子：

        式子里除了输入，剩下的系数都可称为权重（权重和偏置），可以理解权重是控制输入信号重要性的参数，偏置表示了输出信号为1容易程度的参数，假设b=-0.1，只要输入信号的加权总和超过0.1即可，要是b=-20呢。

1、感知机的初级实现

        以上面的式子为例，具体以后者的式子说明。

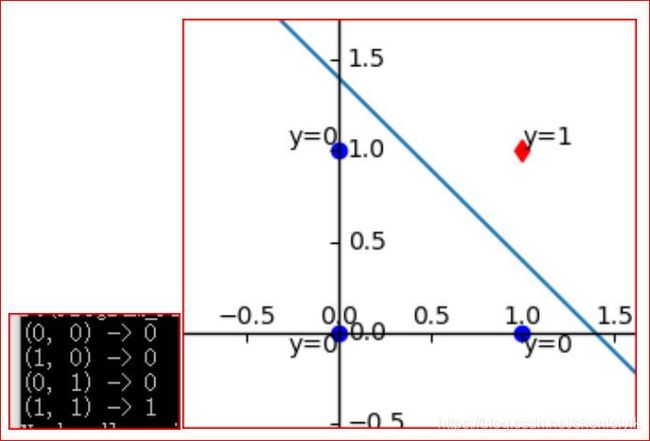
        实现一个两输入的与门或者叫与逻辑，此逻辑表达了输入全为真结果才为真。这里权重应该怎么选择呢？人工算一下，满足条件的参数还是有很多的，比如权重和偏置的参数为（0.5，0.5，-0.7）、（0.5，0.5，-0.8）、（1.0，1.0，-1.0）等等。

# coding: utf-8
import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = AND(xs[0], xs[1])
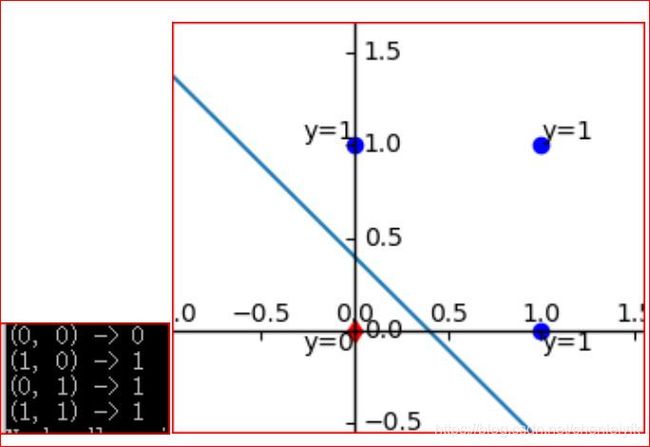
        print(str(xs) + " -> " + str(y))

---

        实现一个两输入的或门或者叫或逻辑：

# coding: utf-8
import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
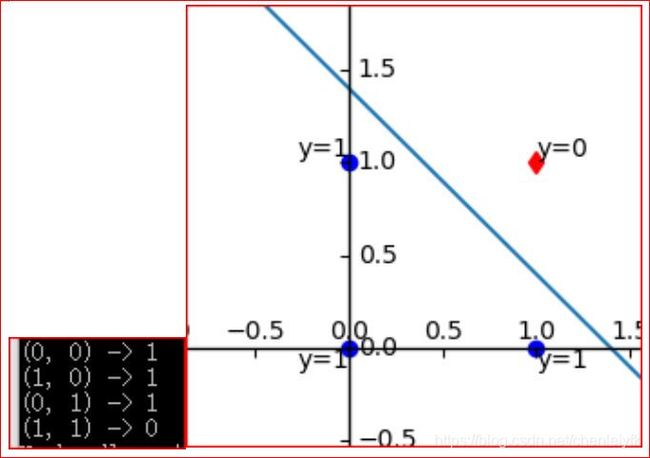
        print(str(xs) + " -> " + str(y))

---

        实现一个两输入的与非门或者叫与非逻辑：

# coding: utf-8
import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

        可以看出，以上三者属于相同构造的感知机，区别仅仅在于权重参数的数值。这里决定感知机参数的是我们，我们通过真值表类似的这种“训练数据”人工想到了参数的值，而深度学习的主题是将这个决定参数数值的工作交由计算机自动进行，学习就是确定合适参数的过程。这种情况下人要做的就是思考感知机的构造。

2 异或门和多层感知机

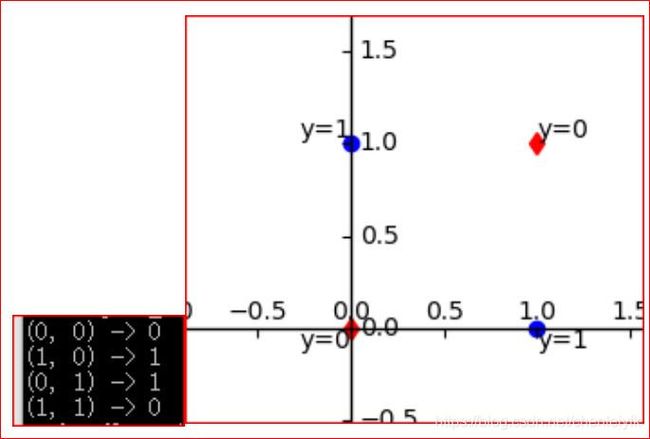
        现在可以思考下异或门和异或逻辑的实现：

        这个图似乎是不可以使用一条直线把y的结果分开了。

        我们知道，直线分割的空间是线性的，即线性空间。如果要是使用曲线的话，分割的思路将会有很多啊，随便把两个红点圈住或是两个蓝点圈住，这就有了非线性空间的分割了。非线性的概念在深度学习中是极其重要的术语，这个日后再论吧（在激活函数的表达中）。

        先来看看这个逻辑如何用感知机实现，这里要思考一个感知机的构造了，我们对异或门的真值表好好分析一下:

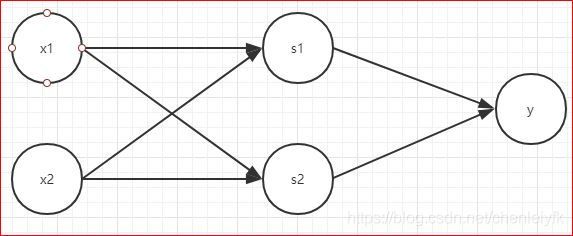
        我们把前面实现的感知机通过这样的叠加，把之前的AND、OR、NAND的实现称之为单层感知机，下面则是两层感知机了：

        之所以称之为两层，有权重的层就只有两层，输入层和隐藏层之间、隐藏层和输出层之间。之间的关系由代码呈现吧。

# coding: utf-8
from and_gate import AND
from or_gate import OR
from nand_gate import NAND
import numpy as np

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

        单层感知机只能表示线性空间，二多层感知机可以表示非线性空间。

        我们的这个构造算是非常简单的，至于好多神经网络的实现也是大神经过了锤炼形成的。不过就算是这个基本的与非门，因为多层感知机的出现，也足以表示非常复杂的逻辑和各类门电路了。学术界确实有人通过与非门来构建计算机过程的，感兴趣的可以看看一本名为《计算机系统要素：从零开始构建现代计算机》。