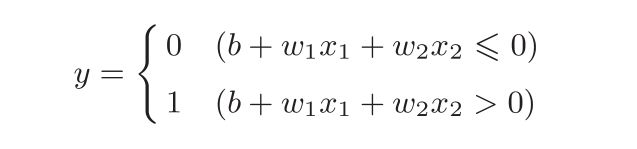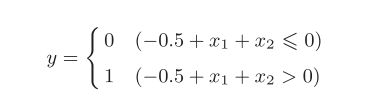深度学习入门笔记:感知机
编程导航:nav.wenancoding.com
个人blog:wenancoding.com
gzh:【问安coding】
定义
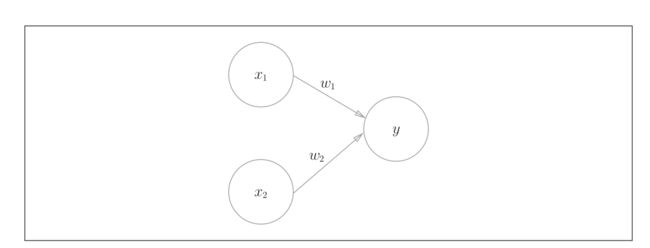
感知机接收多个输入信号,输出一个信号。感知机的信号只有1/0两种取值,0对应“不传递信号”,1对应“传递信号”。
- x 1 ,x 2 是输入信号。
- y是输出信号。
- w 1 、w 2 是权重(w是weight的首字母)。每个变量都有权重,权重越大,对应该权重的信号的重要性就越高。
- 图中的○称为“神经元”或者“节点”。
输入信号被送往神经元时,会被分别乘以固定的权重(w 1 x 1 、w 2 x 2 )。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活” 。这里将这个界限值称为阈值,用符号θ表示。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mjcFiHtn-1651828304002)(https://cos.wenancoding.com/img/20220505152230.png)]
导入权重和偏置
为方便后续的计算,把感知机公式改为:
对比两个公式:虽然有符号不同,但表达的内容是完全相同的。b称为偏置,w 1 和w 2 称为权重。感知机会计算输入信号和权重的乘积,然后加上偏置,如果这个值大于0则输出1,否则输出0。
−θ命名为偏置b,但是请注意,偏置b和权重w 1 、w 2 的作用是不一样的。具体地说,w 1 和w 2 是控制输入信号的重要性的参数,而偏置是调整神经元被激活的容易程度(输出信号为1的程度)的参数。比如,若b为−0.1,则只要输入信号的加权总和超过0.1,神经元就会被激活。但是如果b为−20.0,则输入信号的加权总和必须超过20.0,神经元才会被激活。像这样,偏置的值决定了神经元被激活的容易程度。另外,这里我们将w 1 和w 2 称为权重,将b称为偏置,但是根据上下文,有时也会将b、w 1 、w 2 这些参数统称为权重。
简单的逻辑电路
与门(AND gate)
- 全真为真,其余为假
- 全为1才是1,否则为0
感知机实现与门
公式的不同形式实现,后续以第二种数学公式为主
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
================
AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
与非门(NAND gate)
- NAND:not and,和与门相反。
- 全真为假,其余为真
- 全为1则是0,否则为1
感知机实现与非门
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XunWXk4B-1651828304006)(https://cos.wenancoding.com/img/20220505154434.png)]
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
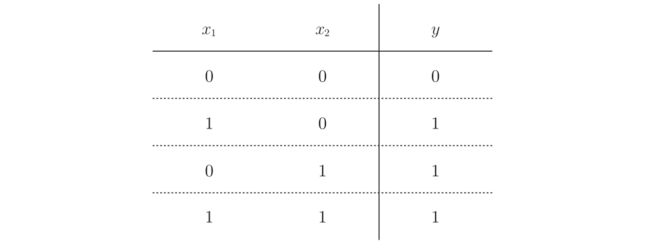
或门(OR gate)
- 有真为真,全假为假
- 有1便是1,全0才是0
感知机实现或门
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PSqiQ6c7-1651828304007)(https://cos.wenancoding.com/img/20220505154434.png)]
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
感知机的局限性
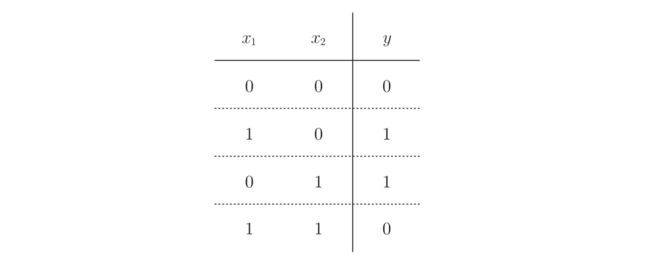
异或门
- 一个真才是真,其余为假
- 只有一个1才是1,其余为0
使用实现与、非与、或的感知机无法实现异或
原因分析
以或门为例,当权重参数(b, w 1 , w 2 ) = (−0.5, 1.0, 1.0)时,可满足或门的条件。此时,感知机可表示为:
分析该分段函数,该直线把平面分为两个值为1或0的区域,直线下方为0,直线上方为1。
类似的,与门,非与门同样可以表示成类似图像。换言之,对于 与、非与、或 我们可以使用一条直线把平面分为两个区域。这种由直线分割而成的空间称为线性空间。
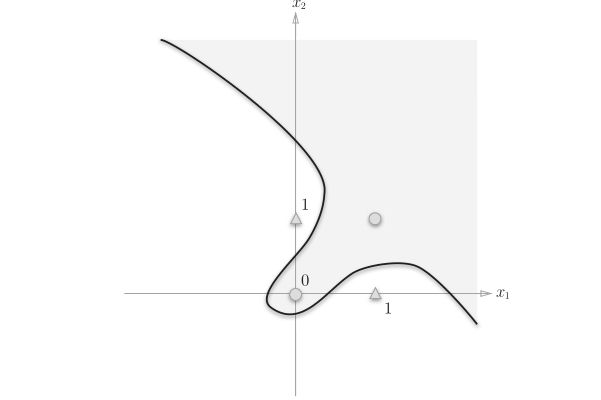
对于异或图像,想要用一条直线将图的○和△分开,无论如何都做不到。事实上,用一条直线是无法将○和△分开的。
只能使用曲线把它们分割开来
这样的曲线分割而成的空间称为非线性空间。
如何实现异或门
- 利用已有的门进行组合叠加即可实现异或门
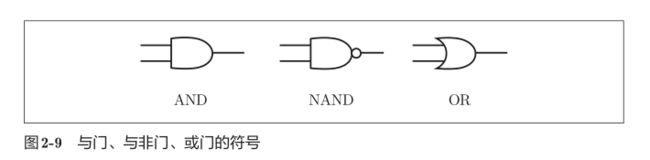
门的符号:
异或门的实现:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OCvoNhc7-1651828304013)(https://cos.wenancoding.com/img/20220505175455.png)]
from and_gate import AND
from or_gate import OR
from nand_gate import NAND
# y的代码
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
多层感知机
对比与、非与、或的感知机
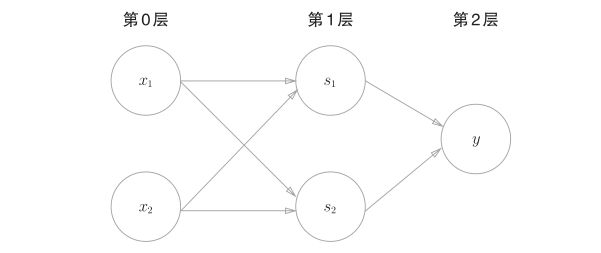
异或的感知机
图中的感知机总共由3层构成,但是因为拥有权重的层实质上只有2层(第0层和第1层之间,第1层和第2层之间),所以称为“2层感知机”。不过,有的文献认为该图感知机是由3层构成的,因而将其称为“3层感知机”。
- 第0层的两个神经元接收输入信号,并将信号发送至第1层的神经元。
- 第1层的神经元将信号发送至第2层的神经元,第2层的神经元输出y。
这种2层感知机的运行过程可以比作流水线的组装作业。第1段(第1层)工人对传送过来的零件进行加工,完成后再传送给第2段(第2层)的工人。第2层的工人对第1层的工人传过来的零件进行加工,完成这个零件后出货(输出)。像这样,在异或门的感知机中,工人之间不断进行零件的传送。通过这样的结构(2层结构),感知机得以实现异或门。这可以解释为“单层感知机无法表示的东西,通过增加一层就可以解决”。也就是说,通过叠加层(加深层),感知机能进行更加灵活的表示。
感知机的拓展
多层感知机可以实现比之前见到的电路更复杂的电路。比如,进行加法运算的加法器也可以用感知机实现。此外,将二进制转换为十进制的编码器、满足某些条件就输出1的电路(用于等价检验的电路)等也可以用感知机表示。实际上,使用感知机甚至可以表示计算机!
内容小结
- 感知机是具有输入和输出的算法。给定一个输入后,将输出一个既定的值。
- 感知机将权重和偏置设定为参数。
- 使用感知机可以表示与门和或门等逻辑电路。
- 异或门无法通过单层感知机来表示。
- 使用2层感知机可以表示异或门。
- 单层感知机只能表示线性空间,而多层感知机可以表示非线性空间。
- 多层感知机(在理论上)可以表示计算机。