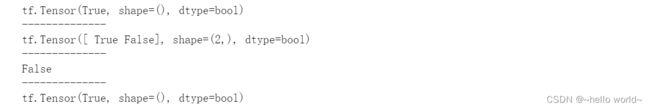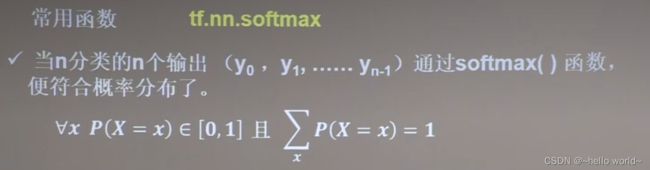TensorFlow基础学习

1、TensorFlow的基本数据类型

  TensorFlow 的基本数据类型包含数值类型、字符串类型和布尔类型。

1.1 数值类型

1.1.1 数组类型的分类

  数值类型根据维度数来区分可分为标量(Scalar)、向量(Vector)、矩阵(Matrix)、张量(Tensor)

  标量：单个的实数，如 1，2, 3 等，维度数为 0，shape 为[ ]

  向量：个实数的有序集合，通过中括号包裹，如[1,2]，[2,3,4]等，维度数为1，长度不定，shape 为[]

  矩阵：行列实数的有序集合，如[[1,2],[3,4]]，每个维度上的长度不定，shape 为[, ]

  张量：所有维度数 > 2的数组统称为张量。张量的每个维度也作轴(Axis)， 一般维度代表了具体的物理含义，其具体物理含义需要由用户自行定义。

  在TensorFlow中，为了表达方便，一般把标量、向量、矩阵也统称为张量，不作区分，需要根据张量的维度数或形状自行判断

1.1.2 张量的创建

import tensorflow as tf

a=tf.constant(1.2) # 标量的创建
print('标量的创建\n',a)
print('-----------------')

b=tf.constant([1,2,3]) # 创建3个元素的向量
print('3个元素的向量\n',b)
print('-----------------')

c=tf.constant([[1,2],[3,4]]) #创建2行2 的矩阵
print('2行2 的矩阵\n',c)
print('-----------------')

d=tf.constant([[[1,2],[3,4]],[[5,6],[7,8]]]) # 创建3维张量
print('3维张量\n',d)

1.1.3 数值精度

  数值类型的张量常用精度类型有 tf.int16、tf.int32、tf.int64、tf.float16、tf.float32、tf.float64 等，其中 tf.float64 即为 tf.double，位越长，精度越高，同时占用的内存空间也就越大。可以通过访问张量的 dtype 成员属性查看张量的保存精度。

1.2 字符串类型

  TensorFlow 还支持字符串(String) 类型的数据，例如在表示图片数据时，可以先记录图片的路径字符串，再通过预处理函数根据路径读取图片张量。在tf.strings模块中，提供了常见的字符串类型的工具函数，如小写化 lower()、拼接join()、长度 length()、切分split()等。通过传入字符串对象即可创建字符串类型的张量。

a=tf.constant('Hello World')
aa=tf.strings.lower(a)
print(aa)

1.3 布尔类型

  为了方便表达比较运算操作的结果，TensorFlow还支持布尔类型的张量。布尔类型的张量只需要传入 Python 语言的布尔类型数据，转换成 TensorFlow 内部布尔型即可，但TensorFlow 的布尔类型和 Python 语言的布尔类型并不等价，不能通用。

a=tf.constant(True) # 创建布尔类型标量
aa=tf.constant([True, False]) # 创建布尔类型向量
print(a)
print('--------------')
print(aa)
print('--------------')
print(a is True) # False---表明TensorFlow的布尔类型和 Python 语言的布尔类型并不等价
print('--------------')
print(a==True) # True---仅数值比较

1.4 类型转换

  对于不符合要求的张量的类型及精度，需要通过tf.cast函数进行强制转换。进行类型转换时，需要保证转换操作的合法性，例如将高精度的张量转换为低精度的张量时，可能发生数据溢出隐患。
语法结构：tf.cast(转换的对象,转换的目标类型)

import numpy as np
a=tf.constant(np.pi,dtype=tf.float16) #创建tf.float16低精度张量
print('tf.float16低精度张量',a)
aa=tf.cast(a,tf.double)#转换为高精度张量
print('转换高精度后的张量',aa)

a1= tf.constant([True, False])
aa1=tf.cast(a1,tf.int32) # 布尔类型转整型
print('布尔类型转整型',aa1)

a2=tf.constant([-1, 0, 1, 2])
aa2=tf.cast(a,tf.bool) # 整型转布尔类型
print('整型转布尔类型',aa2)

1.5 待优化张量

  为了区分需要计算梯度信息的张量与不需要计算梯度信息的张量，TensorFlow 增加了tf.Variable类型用来记录梯度信息。通过 tf.Variable()函数可以将普通张量转换为待优化张量。
  由于梯度运算会消耗大量的计算资源，而且会自动更新相关参数，对于不需要的优化的张量，不需要通过 tf.Variable 封装；相反，对于需要计算梯度并优化的张量，需要通过 tf.Variable 包裹以便 TensorFlow 跟踪相关梯度信息。tf.Variable 类型在普通的张量类型基础上添加了 name，trainable 等属性来支持计算图的构建。name 属性用于命名计算图中的变量；trainable属性表征当前张量是否需要被优化，创建 Variable 对象时是默认启用优化标志，可以设置trainable=False 来设置张量不需要优化；除了通过普通张量方式创建 Variable，也可以直接创建。

a = tf.constant([-1, 0, 1, 2]) # 创建TF张量
aa = tf.Variable(a) # 转换为Variable 型
print('查看Variable类型张量的name属性：\n',aa.name)
print('-------------')
print('查看Variable类型张量的trainable属性：\n',aa.trainable)

# 直接创建 Variable 张量
a = tf.Variable([[1,2],[3,4]]) 
print('查看Variable类型张量的name属性：\n',a.name)
print('-------------')
print('查看Variable类型张量的trainable属性：\n',a.trainable)

2、TensorFlow基础操作（一）

2.1 张量的创建

  在 TensorFlow 中，可以通过多种方式创建张量，如从 Python 列表对象创建，从Numpy 数组创建，或者创建采样自某种已知分布的张量等。

2.1.1 从Python 列表对象和Numpy 数组对象创建张量

  Numpy Array 数组和 Python List 列表是 Python 程序中间非常重要的数据载体容器，很多数据都是通过 Python 语言将数据加载至 Array 或者 List 容器，再转换到 Tensor 类型，通过 TensorFlow 运算处理后导出到 Array 或者 List 容器，方便其他模块调用。通过 tf.convert_to_tensor 函数可以创建新 Tensor，并将保存在 Python List 对象或者Numpy Array 对象中的数据导入到新 tensor 中。

a=tf.convert_to_tensor([1,2]) # 从列表创建张量
print('从列表中创建的张量：',a)
print('-----------------------')
b=tf.convert_to_tensor(np.array([[1,2,3],[4,5,6]])) # 从数组中创建张量
print('从数组中创建的张量：\n',b)

2.1.2 创建全为0或全为1的张量

  将张量创建为全 0 或者全 1 数据是非常常见的张量初始化手段。在线性变换 = + 时，将权值矩阵初始化为全 1 矩阵，偏置 b 初始化为全 0 向量，此时线性变化层输出 = ，因此是一种比较好的层初始化状态。通过 tf.zeros()和 tf.ones()即可创建任意形状，且内容全 0 或全 1 的张量。其中，可以通过 tf.zeros_like, tf.ones_like 新建与某个张量 shape 一致，且内容为全 0 或全 1 的张量。

print('创建全0的向量/n',tf.zeros([2]))
print('------------------')
print('创建全1的向量/n',tf.ones([3]))
print('------------------')
print('创建全0的2×2矩阵\n',tf.zeros([2,2]))
print('------------------')
print('创建全1的3×2矩阵\n',tf.ones([3,2])) 
print('------------------')
a = tf.ones([2,3]) # 创建一个矩阵
print('一个与a形状相同且全为0的矩阵\n',tf.zeros_like(a)) 
print('------------------')
print('一个与a形状相同且全为0的矩阵\n',tf.zeros(a.shape)) 

2.1.3 创建自定义数值张量

  除了初始化为全 0，或全 1 的张量之外，有时也需要全部初始化为某个自定义数值的张量，通过tf.fill(shape, value)可以创建全为自定义数值 value 的张量，形状由 shape 参数指定。

a=tf.fill([3,4],99) # 创建2行2列,元素全为99的矩阵
print(a)

2.1.4 创建已知分布的张量(正态分布与均匀分布)

  正态分布和均匀分布是最常见的分布之一。
  通过 tf.random.normal(shape, mean=0.0, stddev=1.0)可以创建形状为 shape，均值为mean，标准差为 stddev 的正态分布(mean, stddev2)

#正态分布
a=tf.random.normal([2,2], mean=1,stddev=2)
print('创建均值为 1，标准差为 2 的正态分布：\n',a)

  通过 tf.random.uniform(shape, minval=0, maxval=None, dtype=tf.float32)可以创建采样自[minval, maxval)区间的均匀分布的张量

#均匀分布
a=tf.random.uniform([2,4],maxval=10)
print('创建区间为[0,10)的2×4矩阵：\n',a)

2.2 张量的索引与切片

  通过索引与切片操作可以提取张量的部分数据。

2.2.1 索引

  在 TensorFlow 中，索引支持基本的[][]⋯标准索引方式，也支持通过逗号分隔索引号的索引方式。当张量的维度数较高时，使用[][]. . .[]的方式书写不方便，可以采用[,, … , ]的方式索引，它们是等价的。

#以x为4张12×12大小的彩色图片的为例
x=tf.random.normal([4,12,12,3])#创建一个4维的张量
# print(x)
print(x[0])#取第1张图片的数
print(x[0][1])#取第1张图片的第2行
print(x[0][1][2])#取第1张图片，第2行，第3列的数据
print(x[2][1][0][1])#取第3张图片，第2行，第1列的像素，B通道(第2个通道)颜色强度值
print(x[1,9,3])#取第2张图片，第10行，第3列的数据

2.2.2 切片

  与python语法一样，通过[start: end: step]切片方式可以方便地提取一段数据，其中 start 为开始读取位置的索
引，end 为结束读取位置的索引(不包含 end 位)，step 为采样步长。
.
切片格式总结

切片方式	含义
start : end : step	从 start 开始读取到 end(不包含 end)，步长为 step
start : end	从 start 开始读取到 end(不包含 end)，步长默认为 1
start :	从 start 开始读取完后续所有元素，步长默认为 1
start : : step	从 start 开始读取完后续所有元素，步长为 step
: end : step	从 0 开始读取到 end(不包含 end)，步长为 step
: end	从 0 开始读取到 end(不包含 end)，步长默认为 1
: : step	步长为 step 采样
: :	读取所有元素
:	读取所有元素
a, ⋯ ,b	a 维度对齐到最左边，b 维度对齐到最右边，中间的维度全部读取，其他维度按 a/b 的方式读取
a, ⋯	a 维度对齐到最左边，a 维度后的所有维度全部读取，a 维度按 a 方式读取。这种情况等同于 a 索引/切片方式
⋯ ,b	b 维度对齐到最右边，b 之前的所有维度全部读取，b 维度按 b 方式读取
⋯	读取张量所有数据

2.3 维度操作

2.3.1 增、删维度

  增加维度 增加一个长度为 1 的维度相当于给原有的数据添加一个新的维度，维度长度为 1，故数据并不需要改变，仅仅是改变数据的理解方式，因此它其实可以理解为改变视图的一种特殊方式。
  通过 tf.expand_dims(x, axis)可在指定的 axis 轴前可以插入一个新的维度。需要注意的是，tf.expand_dims 的 axis 为正时，表示在当前维度之前插入一个新维度；为负时，表示当前维度之后插入一个新的维度。以[, ℎ , ]张量为例，不同 axis 参数的实际插入位置如图。

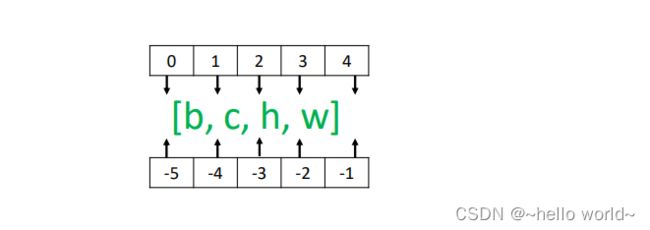
（图来自：龙龙老师《TensorFlow学习》）

#增加维度
x = tf.random.uniform([28,28],maxval=10,dtype=tf.int32)
x = tf.expand_dims(x,axis=2) 
print(x.shape)

x = tf.expand_dims(x,axis=0) 
print(x.shape)

  删除维度 是增加维度的逆操作，与增加维度一样，删除维度只能删除长度为 1 的维度，也不会改变张量的存储。通过 tf.squeeze(x, axis)函数，axis 参数为待删除的维度的索引号。如果不指定维度参数 axis，即 tf.squeeze(x)，那么它会默认删除所有长度为 1 的维度。

x = tf.random.uniform([28,28],maxval=10,dtype=tf.int32)
print('未做维度改变的维度：\n',x.shape)
print('----------------')
#增加维度
x = tf.expand_dims(x,axis=2) 
print('增加维度后的维度：\n',x.shape)
print('----------------')
x = tf.expand_dims(x,axis=0) 
print('增加维度后的维度：\n',x.shape)
print('----------------')
#删除维度
x = tf.squeeze(x, axis=0) 
print('删除维度后的维度：\n',x.shape)
print('----------------')
x = tf.squeeze(x, axis=2) 
print('增加维度后的维度：\n',x.shape)

x = tf.random.uniform([1,28,28,1],maxval=10,dtype=tf.int32)
print('未做维度改变的维度：\n',x.shape)
print('----------------')
x=tf.squeeze(x) 
print('未指定axis参数的维度改变后的维度：\n',x.shape)

2.3.2 交换维度

  改变视图、增删维度都不会影响张量的存储。在实现算法逻辑时，在保持维度顺序不变的条件下，仅仅改变张量的理解方式是不够的，有时需要直接调整的存储顺序，即交换维度(Transpose)。通过交换维度操作，改变了张量的存储顺序，同时也改变了张量的视图。通过使用 tf.transpose(x, perm)函数完成维度交换操作，其中参数 perm表示新维度的顺序 List。

x = tf.random.normal([2,32,32,3])
print('未交换前的维度：\n',x.shape)
print('-----------------')
x=tf.transpose(x,perm=[0,3,1,2]) # 交换维度
print('交换后的维度：\n',x.shape)

2.4 复制数据

  当通过增加维度操作插入新维度后，可能希望在新的维度上面复制若干份数据，满足后续算法的格式要求。

2.4.1 直接复制数据

  可以通过 tf.tile(x, multiples)函数完成数据在指定维度上的复制操作，multiples 分别指定了每个维度上面的复制倍数，对应位置为 1 表明不复制，为 2 表明新长度为原来长度的2 倍，即数据复制一份，以此类推。但tf.tile 会创建一个新的张量来保存复制后的张量，由于复制操作涉及大量数据的读写 IO 运算，计算代价相对较高。

b = tf.constant([1,2]) # 创建向量 b
print('原始数组：\n',b)
print('--------------------')
b = tf.expand_dims(b, axis=0) # 插入新维度，变成矩阵
print('增加维度后的数组：\n',b)
print('--------------------')
b = tf.tile(b, multiples=[2,1]) # 样本维度上复制一份
print('在增加维度后复制数据后的数组：\n',b)

x = tf.range(4)
x=tf.reshape(x,[2,2]) # 创建 2 行 2 列矩阵
print('原始数组：\n',x)
print('--------------------')
x = tf.tile(x,multiples=[1,2]) # 行不复,列制制1份
print('行不复,列制制1份：\n',x)
print('--------------------')
x = tf.tile(x,multiples=[3,1]) # 行复制2份,列不复制
print('行复制2份,列不复制：\n',x)

2.4.2 广播

  广播机制是一种轻量级的张量复制手段，在逻辑上扩展张量数据的形状，但是只会在需要时才会执行实际存储复制操作。Broadcasting 机制通过优化手段避免实际复制数据而完成逻辑运算，从而相对于tf.tile 函数，减少了大量计算代价。制数据若干份，区别在于 tf.tile 会创建一个新的张量，执行复制 IO 操作，并保存复制后的张量数据，而 Broadcasting 并不会立即复制数据，它会在逻辑上改变张量的形状，使得视图上变成了复制后的形状。
  通过 tf.broadcast_to(x, new_shape)函数可以显式地执行自动扩展功能，将现有 shape 扩张为 new_shape。

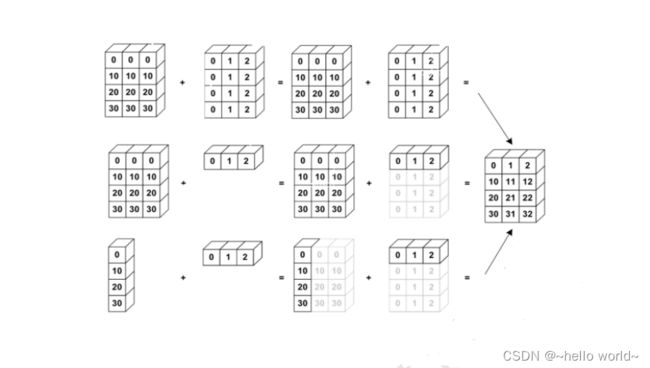
加法运算时自动广播示意图（图来自龙龙老师《TensorFlow学习》）

2.5 数学运算

函数	含义
tf.add、+	加
tf.subtract、-	减
tf.multiply、*	乘
tf.divide、/	除运算
//	整除
%	取余
tf.pow(x, a)、**	乘方运算 = x^a
tf.square(x)	平方运算
tf.sqrt(x)	开放运算
tf.pow(a, x)、**	指数运算^x
tf.exp(x)	e^x
tf.math.log(x)	自然对数lnx运算
任意底数a的对数运算用tf.math.log(x)转换	lnx/lna
tf.matmul(A, B)、A@B	矩阵A,B相乘。TensorFlow 中张量和的维度数可以大于 2。当张量和维度数大于 2 时，TensorFlow 会选择和的最后两个维度进行矩阵相乘，前面所有的维度都视作Batch 维度。

3、TensorFlow基础操作（二）

3.1 合并与分割

3.1.1 合并

  合并是指将多个张量在某个维度上合并为一个张量。张量的合并可以使用拼接和堆叠操作实现。拼接操作并不会产生新的维度，仅在现有的维度上合并，而堆叠会创建新维度。选择使用拼接还是堆叠操作来合并张量，取决于具体的场景是否需要创建新维度。
  拼接 在TensorFlow中，通过 tf.concat(tensors, axis)函数拼接张量，其中tensors保存了所有需要合并的张量 List，axis 参数指定需要合并的维度索引。拼接合并操作可以在任意的维度上进行，唯一的约束是非合并维度的长度必须一致。

a = tf.random.normal([4,35,8])
b = tf.random.normal([6,35,8])
c = tf.concat([a,b],axis=0) 
print('张量a的shape：\n',a.shape)
print('-----------')
print('张量b的shape：\n',b.shape)
print('-----------')
print('张量a,b拼接0轴后的shape：\n',c.shape)

  堆叠 拼接操作直接在现有维度上合并数据，并不会创建新的维度。如果在合并数据时，希望创建一个新的维度，则需要使用 tf.stack 操作。合并数据时，需要创建一个新维度，新维度可以选择放置在任意位置，一般根据大小维度的经验法则，将较大概念的维度放置在较小维度之前。使用 tf.stack(tensors, axis)可以堆叠方式合并多个张量，tensors保存了所有需要合并的张量 List，axis 指定新维度插入的位置，axis 的用法与 tf.expand_dims 的一致，当axis ≥ 0时，在 axis之前插入；当axis < 0时，在 axis 之后插入新维度。tf.stack 进行张量堆叠合并时要求所有待合并的张量 shape 完全一致。

a = tf.random.normal([4,35,8])
b = tf.random.normal([4,35,8])
c = tf.stack([a,b],axis=1)
print('张量a的shape：\n',a.shape)
print('-----------')
print('张量b的shape：\n',b.shape)
print('-----------')
print('张量a,b堆叠1轴后的shape：\n',c.shape)

3.1.2 分割

   合并操作的逆过程就是分割，将一个张量分拆为多个张量。通过 tf.split()函数可以完成张量的分割操作。
语法结构：tf.split(x, num_or_size_splits, axis)
   x ：待分割张量。
   num_or_size_splits：切割方案。当 num_or_size_splits 为单个数值时，表示等长切割的份数；当 num_or_size_splits 为 List 时，List 的每个元素表示分割每份的长度。
   axis 参数：指定分割的维度索。

x = tf.random.normal([10,35,8])
result = tf.split(x, num_or_size_splits=10, axis=0)
len(result) # 返回的列表为 10 个张量的列表
print(result[0])

   特别地，如果希望在某个维度上全部按长度为 1 的方式分割，还可以使用 tf.unstack(x,axis)函数。这种方式是 tf.split 的一种特殊情况，切割长度固定为 1，只需要指定切割维度的索引号即可。

x = tf.random.normal([10,35,8])
result = tf.unstack(x, axis=0)
len(result) # 返回的列表为 10 个张量的列表
print(result[0])

3.2 数据统计

3.2.1 向量范数

  向量范数是表征向量“长度”的一种度量方法，它可以推广到张量上。在神经网络中，常用来表示张量的权值大小，梯度大小等。
  常用的向量范数：

  对于矩阵和张量，同样可以利用向量范数的计算公式，等价于将矩阵和张量打平成向量后计算。在 TensorFlow 中，可以通过 tf.norm(x, ord)求解张量的范数，其中参数
ord 指定为 1、2 时计算 L1、L2 范数，指定为 np.inf 时计算∞ −范数。

x = tf.ones([2,2])
print(x)
print('-------------')
print('L1 范数：',tf.norm(x,ord=1)) # 计算 L1 范数
print('L2 范数：',tf.norm(x,ord=2)) # 计算 L2 范数
print('∞ 范数：',tf.norm(x,ord=np.inf)) # 计算∞范数

3.2.2 最值、均值、和

  通过tf.reduce_max、tf.reduce_min、tf.reduce_mean、tf.reduce_sum 函数可以求解张量在某个维度上的最大、最小、均值、和，也可以求全局最大、最小、均值、和信息。

x = tf.random.uniform([2,2],maxval=100,dtype=tf.int32) # 模型生成概率
print(x)
print('------------')
xx=tf.reduce_max(x,axis=0) 
print('维度0上的最大值：\n',xx)
print('------------')
xx=tf.reduce_max(x,axis=1)
print('维度1上的最大值：\n',xx)
xx=tf.reduce_mean(x,axis=1) 
print('统计1维度上的均值：\n',xx)

  当不指定 axis 参数时，tf.reduce_*函数会求解出全局元素的最大、最小、均值、和等数据

x = tf.random.uniform([2,2],maxval=100,dtype=tf.int32) # 模型生成概率
print(x)
print('------------')
print('统计全局的最大：\n',tf.reduce_max(x))

  通过 tf.argmax(x, axis)和 tf.argmin(x, axis)可以求解在 axis 轴上，x 的最大值、最小值所在的索引号。

3.3 张量比较

  为了计算分类任务的准确率等指标，一般需要将预测结果和真实标签比较，统计比较结果中正确的数量来计算准确率。

函数	比较逻辑
tf.math.greater(a,b)	>
tf.math.less(a,b)	<
tf.math.greater_equal(a,b)	≥
tf.math.less_equal(a,b)	≤
tf.math.not_equal(a,b)	≠
tf.math.is_nan	= nan

3.4 填充与复制

3.4.1 填充

  实际情况中，输入数据的长度，维度长度可能各不相同。为了方便网络的并行计算，需要将不同长度的数据扩张为相同长度。复制的方式可以增加数据的长度，但会破坏原有的数据结构。通常的做法是，在需要补充长度的数据开始或结束处填充足够数量的特定数值，这些特定数值一般代表了无效意义，例如 0，使得填充后的长度满足系统要求，这种操作就叫作填充。
  填充操作可以通过 tf.pad(x, paddings)函数实现，参数 paddings 是包含了多个[Left Padding,Right Padding]的嵌套方案 List。

b = tf.constant([7,8,1,6])
b = tf.pad(b, [[0,2]]) #在b的末尾填充两个0
print(b)

tf.Tensor([7 8 1 6 0 0], shape=(6,), dtype=int32)

3.4.2 复制

  在维度变换中，通过 tf.tile()函数实现长度为 1 的维度复制的功能。tf.tile 函数除了可以对长度为 1 的维度进行复制若干份，还可以对任意长度的维度进行复制若干份，进行复制时会根据原来的数据次序重复复制。

3.5 数据限幅

  怎么实现非线性激活函数 ReLU 的问题。它其实可以通过简单的数据限幅运算实现，限制元素的范围 ∈ [0, +∞)即可。在 TensorFlow 中，通过tf.maximum(x, a)实现数据的下限幅，即 ∈ [, +∞)；可以通过 tf.minimum(x, a)实现数据的上限幅，即 ∈ (−∞,]。更方便地，我们可以使用 tf.clip_by_value 函数实现上下限幅。

x = tf.range(9)
xx1=tf.maximum(x,3) # 下限幅到 3
xx2=tf.minimum(x,6) # 上限幅到 6
print('下限幅到 2',xx1)
print('上限幅到 2',xx2)

xx=tf.clip_by_value(x,3,6) # 限幅为 3-6
print('限幅2-5',xx)

下限幅到 2 tf.Tensor([3 3 3 3 4 5 6 7 8], shape=(9,), dtype=int32)
上限幅到 2 tf.Tensor([0 1 2 3 4 5 6 6 6], shape=(9,), dtype=int32)
限幅2-5 tf.Tensor([3 3 3 3 4 5 6 6 6], shape=(9,), dtype=int32)
​

3.6 常用功能函数

3.6.1 tf.gather

  tf.gather 可以实现根据索引号收集数据。
tf.gather(x,[1,2],axis=0)，表示获取x中0轴索引为1,2 的数据

x = tf.random.uniform([2,3,3],maxval=100,dtype=tf.int32) # 成绩册张量
print(x)
print('-----------')
print(tf.gather(x,[0,2],axis=1))

3.6.2 tf.gather_nd

  通过 tf.gather_nd 函数，可以通过指定每次采样点的多维坐标来实现采样多个点。
  一般地，在使用 tf.gather_nd 采样多个样本时，例如希望采样号班级，个学生，门科目的成绩，则可以表达为[. . . ,[,, ], . . .]，外层的括号长度为采样样本的个数，内层列表包含了每个采样点的索引坐标。

x = tf.random.uniform([4,5,6],maxval=100,dtype=tf.int32)
xx=tf.gather_nd(x,[[1,1,2],[2,2,3],[3,3,4]])
#获取三个数，分别为
#0轴下索引为1、1轴索引为1、2轴索引为2的数
#0轴下索引为2、1轴索引为2、2轴索引为3的数
#0轴下索引为3、1轴索引为3、2轴索引为4的数
print(xx)

tf.Tensor([38 79 40], shape=(3,), dtype=int32)

3.6.3 tf.boolean_mask

  除了可以通过给定索引号的方式采样，还可以通过给定掩码(Mask)的方式进行采样。通过 tf.boolean_mask(x, mask, axis)可以在 axis 轴上根据mask 方案进行采样。注意掩码的长度必须与对应维度的长度一致。

x = tf.random.uniform([4,5,6],maxval=100,dtype=tf.int32)
#获取x中0轴的第一个和最后一个数据
xx=tf.boolean_mask(x,mask=[True, False,False,True],axis=0)
print(xx)

3.6.4 tf.where

  通过 tf.where(cond, a, b)操作可以根据 cond 条件的真假从参数a或b中读取数据。当参数 a=b=None 时，即 a 和 b 参数不指定，tf.where 会返回 cond 张量中所有 True 的元素的索引坐标。

x = tf.random.normal([3,3]) 
print(x)
print('------------')
mask=x>0
x=tf.where(mask) 
print('x中大于0的索引：\n',x)

3.6.5 scatter_nd

  通过 tf.scatter_nd(indices, updates, shape)函数可以高效地刷新张量的部分数据，但是这个函数只能在全 0 的白板张量上面执行刷新操作，因此可能需要结合其它操作来实现现有张量的数据刷新功能。

indices = tf.constant([[1],[3]])
updates = tf.constant([# 构造写入数据，即 2 个矩阵
 [[5,5,5,5],[6,6,6,6],[7,7,7,7],[8,8,8,8]],
 [[1,1,1,1],[2,2,2,2],[3,3,3,3],[4,4,4,4]]
])
# 在 shape 为[4,4,4]白板上根据 indices 写入 updates
x=tf.scatter_nd(indices,updates,[4,4,4])

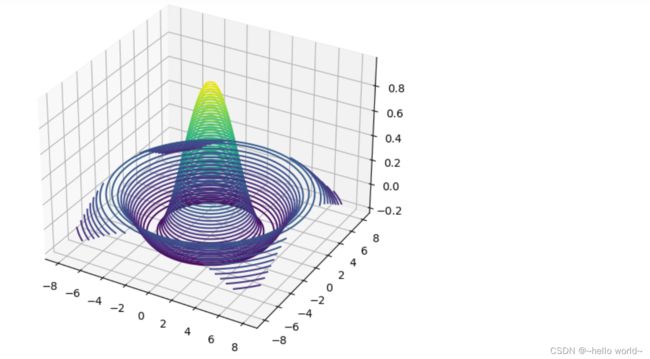
3.6.6 meshgrid

  通过 tf.meshgrid 函数可以方便地生成二维网格的采样点坐标，方便可视化等应用场合。

import matplotlib
from matplotlib import pyplot as plt
# 导入 3D 坐标轴支持
from mpl_toolkits.mplot3d import Axes3D

x = tf.linspace(-8.,8,100) # 设置 x 轴的采样点
y = tf.linspace(-8.,8,100) # 设置 y 轴的采样点
x,y = tf.meshgrid(x,y) # 生成网格点，并内部拆分后返回
z = tf.sqrt(x**2+y**2) 
z = tf.sin(z)/z # sinc 函数实
fig = plt.figure()
ax = Axes3D(fig) # 设置 3D 坐标轴
# 根据网格点绘制 sinc 函数 3D 曲面
ax.contour3D(x.numpy(), y.numpy(), z.numpy(), 50)
plt.show()

4、神经网络中常用的TensorFlow函数

4.1 强制转换—tf.cast(张量名，dtype=数据类型)

  强制转换tensor为指定数据类型：tf.cast(张量名，dtype=数据类型)
.

4.2 记录梯度—tf. Variable()

  tf. Variable()将变量标记为“可训练”，被标记的变量会在反向传播中记录梯度信息。神经网络训练中，常用该函数标记待训练参数。tf.Variable(张量)
.

4.3 常用数学运算

计算张量维度上元素的最小值：tf.reduce_min(张量名)

计算张量维度上元素的最大值：tf.reduce_max(张量名)

计算张量沿着指定维度的平均值：tf.reduce_mean(张量名，axis=操作轴)

计算张量沿着指定维度的和：tf.reduce_sum(张量名，axis=操作轴)

只有维度相同的张量才可以做四则运算
实现两个张量的对应元素相加：tf.add（张量1，张量2)
实现两个张量的对应元素相减：tf.subtract（张量1，张量2)
实现两个张量的对应元素相乘：tf.multiply(张量1，张量2)
实现两个张量的对应元素相除：tf.divide（张量1，张量2)
计算某个张量的平方：tf.square(（张量名)
计算某个张量的n次方：tf.pow（张量名，n次方数)
计算某个张量的开方：tf.sqrt（张量名)
实现两个矩阵的相乘：tf.matmul(矩阵1，矩阵2)

4.4 绑定特征值与标签-----tf.data.Dataset.from _tensor_slices

常用函数：tf.data.Dataset.from _tensor_slices
切分传入张量的第一维度，生成输入特征标签对，构建数据集data = tf.data.Dataset.from_tensor_slices(输入特征,标签)(Numpy和Tensor格式都可用该语句读入数据)

#将特征值与标签绑定
features = tf.constant([12,23,10,17])
labels = tf.constant([0,1,1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features,labels))
print(dataset)
for element in dataset:
    print(element)

4.5 tf.GradientTape----求导

with结构记录计算过程，gradient求出张量的梯度

with tf.GradientTape( ) as tape:
	若干个计算过程
grad=tape.gradient(函数，对谁求导)

4.6 枚举—enumerate

enumerate是python的内建函数，它可遍历每个元素(如列表、元组或字符串)，返回索引和对应的元素，常在for循环中使用。enumerate(列表名)

4.7 换为one-hot——tf.one_hot

独热编码:在分类问题中，常用独热码做标标记类别:1表示是，0表示非。

tf.one hot()函数将待转换数据转换为one-hot形式的数据输出。tf.one_hot(待转换数据, depth=几分类)

4.7 输出符合概率分布——tf.nn.softmax

4.8 参数自更新——assign_sub

4.9 返回最大值索引——tf.argmax

本文仅用于学习交流。