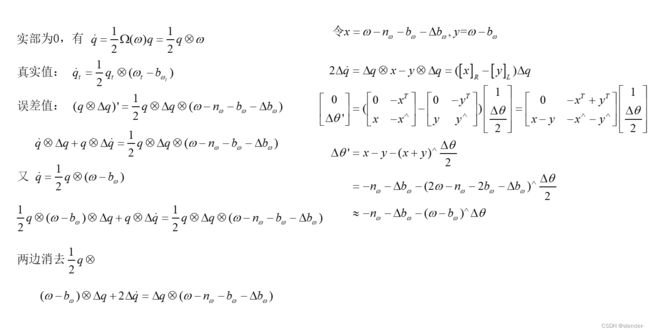从零学习VINS-Mono/Fusion源代码（四）：误差卡尔曼滤波

本节推导误差卡尔曼滤波公式，用以计算误差状态量的置信度。

VINS-Mono/Fusion代码学习系列：
从零学习VINS-Mono/Fusion源代码（一）：主函数
从零学习VINS-Mono/Fusion源代码（二）：前端图像跟踪
从零学习VINS-Mono/Fusion源代码（三）：IMU预积分公式推导
从零学习VINS-Mono/Fusion源代码（四）：误差卡尔曼滤波

误差卡尔曼滤波就是以误差值作为滤波状态量. IMU预积分中使用误差卡尔曼滤波来计算置信度，得到误差的协方差矩阵.
（主要是因为旋转四元数引起的过参数化问题）

1 为什么要用误差卡尔曼滤波？

• IMU预积分中使用四元数表示旋转，但是四元数是过参数化的，需要用4x4的矩阵来描述置信度；在误差卡尔曼滤波中，用旋转向量作为参数，这样就可以用3x3的协方差矩阵来衡量旋转的置信度.
• 误差通常是很小的，接近0，这样就避免了旋转向量的周期性问题.
• 误差量很小，可以忽略二阶导数的计算，只计算一阶导数更快.
• 误差变化很慢，用卡尔曼滤波进行状态修正时，可以降低观测频率.

2 连续时间IMU误差状态传递

vins论文公式：

推导速度：

推导姿态：

3 离散时间预积分误差传递

同样，利用中值积分推算，在两帧IMU时刻之间，认为零偏不变。

4 IMU零偏建模

在上面的推导中认为IMU零偏是不变的，但是VINS优化过程中，零偏也会被优化，导致对应的IMU预积分可能需要重新计算。因此，利用误差雅克比对IMU预积分进行修正。

为了方便维护，VINS代码中建立了一个15x15的雅克比矩阵，在初始状态下为单位阵I：

5 代码阅读

在integration_base.h头文件中找到类IntegrationBase，看到它的构造函数：它依赖于初始时刻的加速度计和陀螺零偏；维护了15x15的jacobian矩阵，初始值为单位阵；构造误差协方差矩阵covariance，初始为0.
noise对应噪声协方差矩阵V.

IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
                    const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
        : acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},
          linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg},
            jacobian{Eigen::Matrix<double, 15, 15>::Identity()}, covariance{Eigen::Matrix<double, 15, 15>::Zero()},
          sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}

    {
        noise = Eigen::Matrix<double, 18, 18>::Zero();
        noise.block<3, 3>(0, 0) =  (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
        noise.block<3, 3>(3, 3) =  (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
        noise.block<3, 3>(6, 6) =  (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
        noise.block<3, 3>(9, 9) =  (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
        noise.block<3, 3>(12, 12) =  (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();
        noise.block<3, 3>(15, 15) =  (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
    }

在midPointIntegration()中，中值积分更新完状态量后，更新协方差阵和雅克比矩阵，套用基于中值积分的离散时间预积分误差传递公式：

		if(update_jacobian)
        {
            Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
            Vector3d a_0_x = _acc_0 - linearized_ba;
            Vector3d a_1_x = _acc_1 - linearized_ba;
            Matrix3d R_w_x, R_a_0_x, R_a_1_x;

            R_w_x<<0, -w_x(2), w_x(1),
                w_x(2), 0, -w_x(0),
                -w_x(1), w_x(0), 0;
            R_a_0_x<<0, -a_0_x(2), a_0_x(1),
                a_0_x(2), 0, -a_0_x(0),
                -a_0_x(1), a_0_x(0), 0;
            R_a_1_x<<0, -a_1_x(2), a_1_x(1),
                a_1_x(2), 0, -a_1_x(0),
                -a_1_x(1), a_1_x(0), 0;

            MatrixXd F = MatrixXd::Zero(15, 15);
            F.block<3, 3>(0, 0) = Matrix3d::Identity();
            F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt + 
                                  -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
            F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
            F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
            F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
            F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
            F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
            F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt + 
                                  -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
            F.block<3, 3>(6, 6) = Matrix3d::Identity();
            F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
            F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
            F.block<3, 3>(9, 9) = Matrix3d::Identity();
            F.block<3, 3>(12, 12) = Matrix3d::Identity();
            //cout<<"A"<

            MatrixXd V = MatrixXd::Zero(15,18);
            V.block<3, 3>(0, 0) =  0.25 * delta_q.toRotationMatrix() * _dt * _dt;
            V.block<3, 3>(0, 3) =  0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * _dt * 0.5 * _dt;
            V.block<3, 3>(0, 6) =  0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
            V.block<3, 3>(0, 9) =  V.block<3, 3>(0, 3);
            V.block<3, 3>(3, 3) =  0.5 * MatrixXd::Identity(3,3) * _dt;
            V.block<3, 3>(3, 9) =  0.5 * MatrixXd::Identity(3,3) * _dt;
            V.block<3, 3>(6, 0) =  0.5 * delta_q.toRotationMatrix() * _dt;
            V.block<3, 3>(6, 3) =  0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * 0.5 * _dt;
            V.block<3, 3>(6, 6) =  0.5 * result_delta_q.toRotationMatrix() * _dt;
            V.block<3, 3>(6, 9) =  V.block<3, 3>(6, 3);
            V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
            V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;

            //更新雅克比和协方差
            jacobian = F * jacobian;
            covariance = F * covariance * F.transpose() + V * noise * V.transpose();
        }