李宏毅机器学习-HW1

---

前言

李宏毅机器学习课程第一个作业

链接: 官方实验指导.
参考：link.

第一次写博客，记录一下学习李宏毅的机器学习实验的过程！目的是梳理和记录思路。不得不说，写博客是一个很好的学习方式。
第一个作业是最基础的线性回归任务，重点在于对于原始数据的处理和线性回归训练的过程。

---

一、分析目标

目标为由前9 个小时的18 个features (包含PM2.5)预测第10 个小时的PM2.5。使用的模型为linear regression。

---

二、数据预处理

这一步分为三个部分：

1. 数据的提取和简单处理：提取数据，将数据中不能处理的文字替换成数字
2. 特征提取：划分特征与标签
3. 训练集和验证集的切分

1.初步处理

首先，原始数据纵列为12个月每月取20天，每天18个特征，横列为24h的值。（12×20×19）×24。观察原始数据发现需要进行的处理为：

• 只取第三列之后的值
• 将NR替换为数字

import pandas as pd
import numpy as np
import math

data = pd.read_csv('./data/train.csv', encoding = 'big5')
data = data.iloc[:, 3:]#行列切片
data[data == 'NR'] = 0
raw_data = data.to_numpy()

结果：
data:

raw_data:

可以看到虽然在读取数据时没有删除第一行，但是在转为numpy后第一行被删除。

2.特征提取

（1）更改数据的排列方式，目的是让数据更加清晰容易获取。
将原始数据（18×20×12）×24，依照每个月份重组成12 个18 (features) × 480 (hours) 的数据。

• 输入：行（12（month）* 20（day）* 18（feature））×列（24（hour））
• 输出：以字典存储
  12（month）×【行（18（features））×列（20（day）×24（hour））】

month_data = {}
for month in range(12):
    sample = np.empty([18, 480])
    for day in range(20):
        sample[:, day * 24 : (day + 1) * 24] = raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]
    month_data[month] = sample

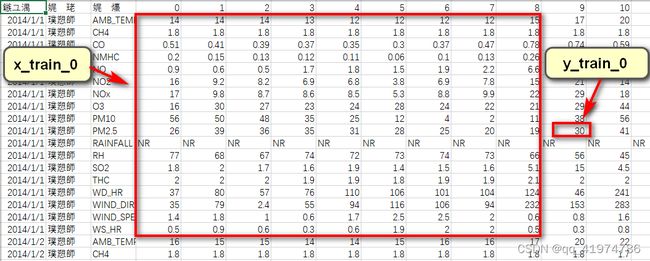
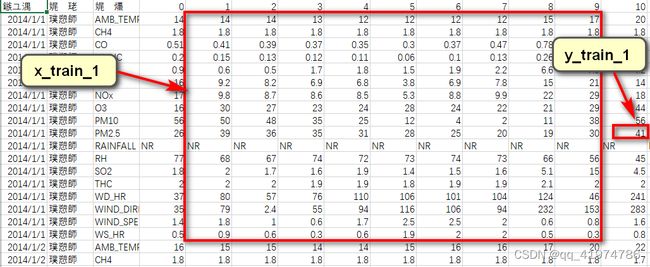
（2）使用滑动窗口的思想进行数据的提取。目的是将数据划分为用于训练的特征和对应预测的标签。
每九个小时的所有特征作为一组数据（所以每个月有480-9=471组），第10个小时PM2.5值的作为对应的target。

输出：x,y

• x：特征 行（12（month）*471（组））×列（18（feature）*9（hour））
• y：标签 行（12（month）*471（组））×1

至此可以得到对应的行表示组数的特征和标签。

x = np.empty([12 * 471, 18 * 9], dtype = float)
y = np.empty([12 * 471, 1], dtype = float)
for month in range(12):
    for day in range(20):
        for hour in range(24):
            if day == 19 and hour > 14:
                continue
            x[month * 471 + day * 24 + hour, :] = month_data[month][:,day * 24 + hour : day * 24 + hour + 9].reshape(1, -1) #vector dim:18*9 (9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9)
            y[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9] #value

3.Normalize和切分训练集和验证集

（1）normalize
数据的标准化目的： link.

mean_x = np.mean(x, axis = 0) #18 * 9
std_x = np.std(x, axis = 0) #18 * 9
for i in range(len(x)): #12 * 471
    for j in range(len(x[0])): #18 * 9
        if std_x[j] != 0:
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]

（2）切分训练集与数据集
取80%为训练集，20%为测试集。
训练集：1131组数据
验证集：4521组数据

x_train_set = x[: math.floor(len(x) * 0.8), :]
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8): , :]
y_validation = y[math.floor(len(y) * 0.8): , :]

至此完成数据预处理部分

---

三、训练

在这一步中，使用事先分出的训练集进行训练。使用线性回归进行训练，本次实验使用Adagrad算法。
链接: link.

sgd算法：

Adagrad算法：
Adagrad算法与普通的sgd算法区别在于标出重点处。
简单来讲，设置全局学习率之后，每次通过全局学习率逐参数的除以历史梯度平方和的平方根，使得每个参数的学习率不同。

loss function选择root mean square error

import numpy as np
from dataload import x_train_set,y_train_set
dim = 18 * 9 + 1#存在常数项，故需要加一
w = np.zeros([dim, 1])#保存模型参数
x_train_set = np.concatenate((np.ones([4521, 1]), x_train_set), axis = 1).astype(float)
learning_rate = 100
iter_time = 10000
adagrad = np.zeros([dim, 1])#使用adagrad算法更新学习率
eps = 0.0000000001
#因为新的学习率是learning_rate/sqrt(sum_of_pre_grads**2),而adagrad=sum_of_grads**2,所以处在分母上而迭代时adagrad可能为0，所以加上一个极小数，使其不除0
for t in range(iter_time):
loss1=[]
time=[]
for t in range(iter_time):
    loss = np.sqrt(np.sum(np.power(np.dot(x_train_set, w) - y_train_set, 2))/4521)#rmse
    loss1.append(loss)
    time.append(t)
    #每一百次迭代输出一次损失
    if(t%100==0):
        print(str(t) + ":" + str(loss))
    gradient = 2 * np.dot(x_train_set.transpose(), np.dot(x_train_set, w) - y_train_set) #dim*1
    adagrad += gradient ** 2
    w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
np.save('./weight.npy', w)

---

四、验证

使用验证集进行验证。载入验证集，使用同样的方法计算预测值，计算loss。

import numpy as np
from dataload import x_validation,y_validation

w = np.load('./weight.npy')
x_validation = np.concatenate((np.ones([1131, 1]), x_validation), axis=1).astype(float)
ans_y = np.dot(x_validation, w)
loss = np.sqrt(np.sum(np.power(ans_y - y_validation, 2)) / 1131)
print(loss)

结果：
训练集中最后一次迭代的loss为5.72
测试集中输出的loss为5.66

---

五、预测

预测test.csv中的PM2.5并保存在文件中。

1.数据预处理

首先将数据预处理成与训练过程中相同的数据格式

• 输入：行（4320）× 列（9）
• 输出：行（240（组））× 列（18（feature）*9（hour））

为了方便处理加上了一行

import pandas as pd
import numpy as np
import csv

test_data = pd.read_csv('./data/test.csv', encoding = 'big5')
test_data = test_data.iloc[:, 2:]  # 取csv文件中的全行数即第3列到结束的列数所包含的数据
test_data[test_data == 'NR'] = 0  # 将testdata中的NR替换为0
print(test_data)
test_data = test_data.to_numpy()  # 将其转换为数组
print(test_data)
test_x = np.empty([240, 18 * 9], dtype = float)
for i in range(240):  # 共240个测试输入数据
    test_x[i, :] = test_data[18 * i: 18 * (i + 1), :].reshape(1, -1)

# 下面是Normalize,且必须跟training data是同一种方法进行Normalize
mean_x = np.mean(test_x, axis = 0) #18 * 9
std_x = np.std(test_x, axis = 0) #18 * 9
for i in range(len(test_x)):
    for j in range(len(test_x[0])):
        if std_x[j] != 0:
            test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
test_x = np.concatenate((np.ones([240, 1]), test_x), axis=1).astype(float)  # 在test_x前面拼接一列全1数组，构成24

2.预测

# 进行预测
w = np.load('weight.npy')
ans_y = np.dot(test_x, w)  # test data的预测值ans_y=test_x与W的积

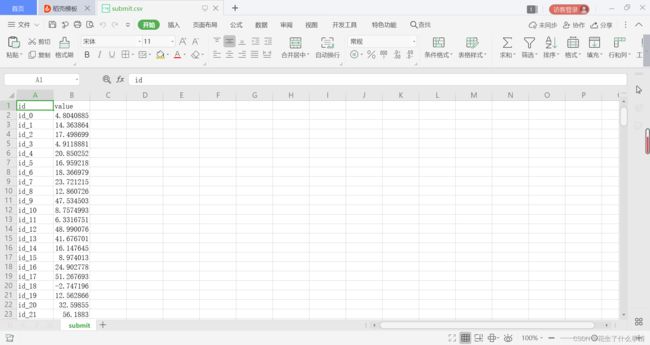
3.写入文件

# 将预测结果填入文件当中
with open('./data/submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    print(header)
    csv_writer.writerow(header)
    for i in range(240):
        row = ['id_' + str(i), ans_y[i][0]]
        csv_writer.writerow(row)
        print(row)

得到的结果如下

---

总结

至此完成任务

本次作业的主要关注点在于:

• 对于原始数据的处理，包括对于无法处理的文字的修改，数据的特征提取。
• 文件的读写。
• 线性回归训练过程。