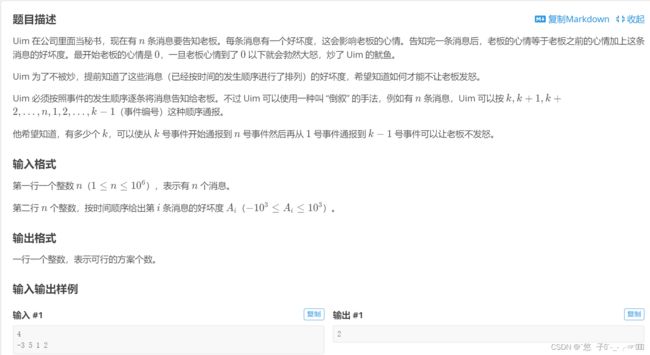
P2629 好消息，坏消息（彻底弄懂单调队列和前缀和）

一、题目：

传送门：P2629 好消息，坏消息 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

二、题解及思路

思路：把数据变成环状，结合前缀和和单调队列求得k的个数。

具体过程：

通过题目给的数据：  -3 5 1 2 

我们可以把数据变成环状：-3 5 1 2  -3 5 1

然后得到前缀和：-3 2 3 5 2 7 8

这题就变成了让我们找到有多少个k使得从sum[k]到sum[k+n]的每个区间和都大于0，

如案例中n=4,

k=1时,要我们求【1，4】的每个区间和是否都大于0，即要求sum【1，1】>0? sum【1，2】>0?sum【1，3】>0？sum【1，4】>0？

注意要求的是区间和大不大于0,而且只要中途出现了小于0的区间和（不包括0哦）就代表Uim被老板炒了鱿鱼。

同理，k=2时有【2，5】，k=3时有【3，6】，k=4时有【4，7】

为了方便理解，我列举了以下表格

如我们要求案例: （其中n=4）(如果在某个区间sum<0，Uim就被老板炒了鱿鱼）

k值	要判断的区间	sum[k,k+1]	k+2	.....	k+4	Uim情况
1	【1，4】	-3<0				被炒
2	【2，5】	2>0	3>0	5>0	2>0	√
3	【3，6】	3>0	5>0	2>0	7>0	√
.....	.....	.....	...	...	....	×

这样我们就可以用O(）的时间复杂度去判断每一个k在sum[k]到sum[k+n]的每个区间有没有小于0的区间和。

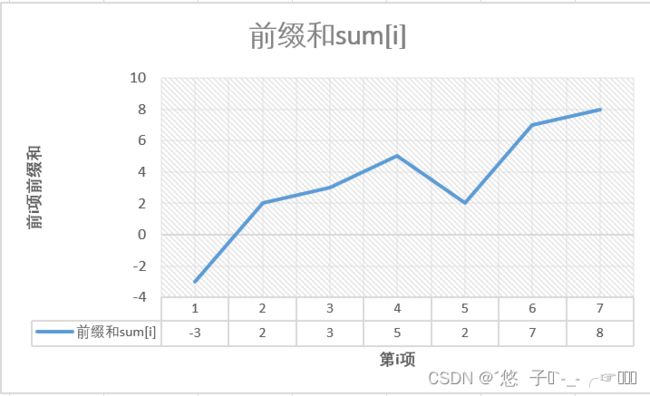
我们还可以优化算法吗？我们先来看一个前缀和的关系图。

 通过这个图我们可以清晰的看出整个区间和的单调性，暴力解法就是去找有没有小于0的部分。遇到小于0就停下，并证明了这个k不行。

我们也没有更好的思路呢？

比如在已知的前缀和的单调性折线找到最小的那个点，然后计算它是否小于0？

这样就行了吗？

好像真的可以，经过我们思考发现，对于每一个sum的前缀和，不管它是如何递增如何递减的，我们只要保证前缀和不出现小于0,确实只要通过判断最低点小不小于0就可以判断这个k能不能成立。

 下面我们来了解什么是单调队列：
        单调队列，顾名思义，是一种具有单调性的队列。众所周知，单调性有单调递增和单调递减两种，相应的单调队列也分为单调递增队列和单调递减队列两种。

单调递增队列：保证队列头元素一定是当前队列的最小值，用于维护区间的最小值。

单调递减队列：保证队列头元素一定是当前队列的最大值，用于维护区间的最大值。

 实现流程：
实现单调队列，主要分为三个部分：

去尾操作 ：队尾元素出队列。当队列有新元素待入队，需要从队尾开始，删除影响队列单调性的元素，维护队列的单调性。(删除一个队尾元素后，就重新判断新的队尾元素)
去尾操作结束后，将该新元素入队列。

删头操作 ：队头元素出队列。判断队头元素是否在待求解的区间之内，如果不在，就将其删除。（这个很好理解呀，因为单调队列的队头元素就是待求解区间的极值）

取解操作 ：经过上面两个操作，取出 队列的头元素 ，就是 当前区间的极值 。
 

所以我们引入了单调队列，去维护它区间最小前缀和。

对于每一个以某个k为起点，以k+n为终点的区间，从要判断区间里的每一项前缀和大于0转变成了只要去判断区间里最小前缀和小不小于0，来决定k的有效性。

创建一个相对于队首来说单调递增的队列，那队首不正时我们要找的最低点吗？即区间最小前缀和，这个k成不成立就只要看它大不大于等于0，小不小于0？

因为每个元素只进行了两次（因为为环状）或一次入队出队操作，所以我们只要O(n)的时间复杂度就可以解出这道题。

三、代码

#include
using namespace std;
int rear,front=1,ans,n;
long long que[2000005],a[2000005],sum[2000005];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		a[n+i]=a[i];	//构建环状[1,2n-1]值 
		sum[i]=sum[i-1]+a[i];//构造n项前缀和 
	}
	for(int i=n+1;i<=2*n-1;i++){
		sum[i]=sum[i-1]+a[i];//构造环状前缀和 [1,2n-1]
	}
	for(int i=1;i<=2*n-1;i++) {
	   while(front<=rear&&max(i-n+1,1)>que[front])front++;//控制要判断的区间 ，且保证最小为1
	   while(front<=rear&&sum[i]<=sum[que[rear]])rear--;//控制区间和的单调性 
	   que[++rear]=i;
		 if (i-n+1>0&&sum[que[front]]-sum[i-n]>=0)ans++;//如果最小的区间和都大于0说明都大于0 
		
	}
	cout<

四、附上结果：

 创作不易，如果觉得这个题解对你解题有帮助能否点个赞呢？当然也不拒绝白嫖！

如果觉得哪里有什么需要改进或不好的地方，可以私聊或评论区留言！感谢观看！