机器学习算法之K均值算法(KMeans)
文章目录
-
- KMeans原理
-
- 算法步骤
- 伪代码
- KMeans算法的优缺点
-
- 优点
- 缺点
- KMeans中类别数K如何确定 ?
-
- 按需选择
- 观察法
- 手肘法
- Gap Statistic方法
- KMeans算法的改进——KMean++
- Reference
KMeans原理
KMeans是常见的聚类算法,属于非监督学习。
算法步骤
假设我们现在有数据集 D D D:
D = { x 1 , x 2 , . . . , x m } D=\{ x_1, x_2, ..., x_m\} D={x1,x2,...,xm}
- 随机选择 k k k 个样本作为初始聚类中心, a = a 1 , a 2 , . . . , a k a=a_1,a_2,...,a_k a=a1,a2,...,ak
- 对于每个样本 x i x_i xi 分别计算它到 k k k 个聚类中心的距离,将它归类到离它最近的聚类中心
- 对于每个类别 C j C_j Cj, 计算该类别所有样本的均值作为新的聚类中心。新的样本中心为, a j = 1 n ∑ x i ∈ C j x i a_j=\displaystyle\frac{1}{n}\displaystyle\sum_{x_i\in {C_j}}{x_i} aj=n1xi∈Cj∑xi
- 重复2-3,直到到达某个终止条件,比如达到一定的迭代次数或者变化不超过某个阈值。
伪代码
有m个d维的样本点
生成k个初始聚类中心
while(iteration < t){
for(int i = 0; i < m; i++){
for(int j = 0; j < k; j++){
计算每个样本点到每个聚类中心的距离, 此层for循环时间复杂度是 O(d)
}
}
for(int i = 1; i < k; i++){
更新每个类的聚类中心
}
}
时间复杂度
如上伪代码所描述,时间复杂度是O(tmkd), t是迭代次数, m是样本数,k是类别数,d是数据维度。
KMeans算法的优缺点
优点
- 容易理解,聚类效果不错
- 处理大数据集的时候,该算法可以保证较好的伸缩性;
- 当簇近似高斯分布的时候,效果非常不错;
- 算法复杂度低。
缺点
- K 值需要人为设定,不同 K 值得到的结果不一样;
- 对初始的聚类中心敏感,不同初始化方式会得到不同结果;
- 对异常值敏感;
- 样本只能有一种类标签,不适合多标签分类任务;
- 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类、具有结构化特征的分类。
KMeans中类别数K如何确定 ?
按需选择
比如某游戏公司把玩家按水平分为4类:王者,黄金,白银,青铜;按年龄把人群分为5类:老年、中年、青年、儿童、婴儿。
按需选择虽然合理,但是未必能保证在做K-Means时能够得到清晰的分界线。
观察法
说白了就是目测 ,就是用肉眼看,看这些点大概聚成几堆。这个方法虽然简单,但是同时也模棱两可。比如下面两图,你可以认为分成2类,也可以觉得分成3类 ,完全因人而异:


观察法的另一个缺陷就是:原始数据维数要低,一般是两维(平面散点)或者三维(立体散点),否则人类肉眼则无法观察。对于高维数据,我们通常利用PCA降维,然后再进行肉眼观察。
手肘法
当KMeans算法完成后,我们得到 k 个聚类中心 a 1 , a 2 , . . a k a_1,a_2,..a_k a1,a2,..ak 和 k 个类别 C 1 , C 2 , . . . , C k C_1, C_2, ..., C_k C1,C2,...,Ck , 通常我们把所有样本点到它所在的聚类的中心点的距离的和作为对模型的度量,记作 D k D_k Dk:
D k = ∑ i = 1 k ∑ x j ∈ C i ∥ x i − a i ∥ D_k=\sum_{i=1}^{k}{\sum_{x_j\in C_i}{\| x_i-a_i\| }} Dk=i=1∑kxj∈Ci∑∥xi−ai∥
这里距离可以采用欧式距离。对于不同的 k k k,最后我们会得到不同的中心点和聚类,所有会有不同的度量。
我们把上面的例子用不同的 k k k 去计算,会得到不同的结果。把 k k k 作为横坐标, D k D_k Dk作为纵坐标,我们可以得到下面的折线。
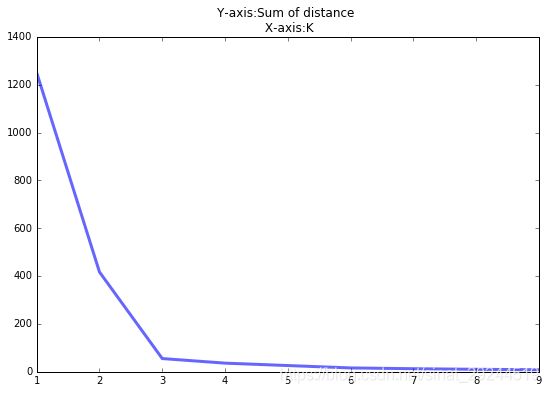
从图中可以看出 k k k 越大,距离和越小。当 k < 3 k < 3 k<3 时,曲线急速下降;当 k > 3 k > 3 k>3 时,曲线趋于平稳,通过手肘法我们认为拐点 3 就像是我们的肘部一, 为 k k k 的最佳值。
Gap Statistic方法
手肘法的缺点在于需要人工看不够自动化,所以我们又有了 Gap statistic 方法,这个方法出自斯坦福大学的几个学者的论文:Estimating the number of clusters in a data set via the gap statistic
这里继续需要用到手肘法的 D k D_k Dk, Gap Statistic的定义是:
G a p ( k ) = E ( l o g D k ) − l o g D k Gap(k)=E(logD_k)-logD_k Gap(k)=E(logDk)−logDk
这里 E ( l o g D k ) E(logD_k) E(logDk) 指的是 l o g D k logD_k logDk 的期望, E ( l o g D k ) E(logD_k) E(logDk) 通常通过蒙特卡洛模拟产生。 具体来说就是我们在样本里所在的矩形区域中(高维的话就是立方体区域)按照均匀分布随机地产生和原始样本数一样多的随机样本,并对这些随机样本做K-Means,从而得到一个 D k D_k Dk 。如此往复多次,通常20次,我们可以得到20个 l o g D k logD_k logDk 。对这20个数值求平均值,就得到了 E ( l o g D k ) E(logD_k) E(logDk) 的近似值。最终可以计算Gap Statisitc。而Gap statistic取得最大值所对应的 k k k 就是最佳的 k k k。
用上图的例子,我们计算了K=1,2,…9对应的Gap Statisitc.
KMeans算法的改进——KMean++
KMeans++ 算法是对KMeans算法的最知名的一种改进方法。主要是对初始选择 k k k 个聚类中心的方法进行改进,本质是选择尽可能分散的点作为聚类中心。KMeans****算法是随机从样本选择 k k k 个,而KMeans++ 算法是这样选择 k k k 个初始聚类中心的:
Step 1 : 从数据集随机选取一个样本作为第一个聚类中心 a 1 a_1 a1
Step 2 : 首先对每个样本计算它到现有聚类中心中最近的一个的距离,记作 D ( x ) D(x) D(x), 该样本被选中作为下一个聚类中心的概率记作 P ( x ) = D 2 ( x ) ∑ i = 1 m D 2 ( x i ) P(x)=\displaystyle \frac{D^2(x)}{\displaystyle \sum_{i=1}^{m} D^2(x_i)} P(x)=i=1∑mD2(xi)D2(x)。然后按照轮盘法选出下一个聚类中心。
Step3 : 重复 Step 2 直到选出 k k k 个聚类中心。
比如在上图所示样本中我们通过观察法想把它们聚成两类,即设定 k = 2 k=2 k=2, KMeans++将按照如下步骤选取 2 2 2 个聚类中心:
步骤1:
我们随机选择一个样本,比如 a 1 = 2 a_1=2 a1=2 作为第1个聚类中心;
步骤2:
那么我们可以计算出,各个点到 a 1 a_1 a1 的距离以及相应概率:
| 样本点 | D ( x i ) \bm{ D(x_i)} D(xi) | D 2 ( x i ) \bm {D^2(x_i)} D2(xi) | P ( x i ) \bm {P(x_i)} P(xi) | p i \bm p_i pi (sum probabilities) |
|---|---|---|---|---|
| 1 | 1 1 1 | 1 1 1 | 0.0125 0.0125 0.0125 | 0.0125 0.0125 0.0125 |
| 2 | 0 0 0 | 0 0 0 | 0 0 0 | 0.0125 0.0125 0.0125 |
| 3 | 2 \sqrt 2 2 | 2 2 2 | 0.025 0.025 0.025 | 0.0375 0.0375 0.0375 |
| 4 | 1 1 1 | 1 1 1 | 0.0125 0.0125 0.0125 | 0.0500 0.0500 0.0500 |
| 5 | 2 5 2\sqrt 5 25 | 20 20 20 | 0.25 0.25 0.25 | 0.3000 0.3000 0.3000 |
| 6 | 13 \sqrt {13} 13 | 13 13 13 | 0.1625 0.1625 0.1625 | 0.4625 0.4625 0.4625 |
| 7 | 5 5 5 | 25 25 25 | 0.3125 0.3125 0.3125 | 0.7750 0.7750 0.7750 |
| 8 | 3 2 3\sqrt 2 32 | 18 18 18 | 0.225 0.225 0.225 | 1.0000 1.0000 1.0000 |
所谓轮转法就是对现在各个样本点所属区间进行划分,比如我们设定 p 0 = 0 p_0 = 0 p0=0 , 那么第 i i i 个样本点的区间范围就是 p i − 1 ≤ p < p i p_{i-1} \le p < p_i pi−1≤p<pi, 比如我们有 8 个样本,我们就这样把 [ 0 , 1 ) [0, 1) [0,1) 划分成了八个区间。然后我们随机生成一个 [ 0 , 1 ) [0, 1) [0,1)区间的数字,看它落在哪个区间,就选哪个区间对应的样本点作为第二个聚类中心。
比如我们现在生成了一个 [ 0 , 1 ) [0, 1) [0,1) 区间的随机数 p = 0.281954791393 p=0.281954791393 p=0.281954791393,满足 p ∈ [ p 4 , p 5 ) p \in {[p_4, p_5)} p∈[p4,p5), 因此选择第5个样本点作为第二个聚类中心,即 a 2 = 5 a_2=5 a2=5。至此,已完成 k k k 个聚类中心的选择。KMeans++算法 的其余步骤与KMeans算法相同。
我们可以看到,KMeans++算法选择的两个初始聚类中心2和5的确距离较远,这个和一开始说的本质是选择尽可能分散的点作为聚类中心是一致的。
Reference
【sofasofa.io】K-means怎么选K?
【机器学习】K-means(非常详细)—— 知乎 阿泽
K-means聚类算法的三种改进(K-means++,ISODATA,Kernel K-means)介绍与对比 —— 博客园 Yixuan-Xu

