医学图像处理医学图像处理-卷积神经网络卷积神经网络_深度学习入门 | 第四章:卷积神经网络基础(1)...
在前面的章节中,介绍了全连接神经网络的相关知识,本章将介绍一种全新的神经网络结构——卷积神经网络(Convolutional Neural Network,CNN)。在很多场合,都能看到卷积神经网络的身影,如图像识别、自然语言处理、语音识别等,但CNN最主要的应用还是在图像识别领域。因此,本章将基于图像识别问题来讲解卷积神经网络的原理。
相对于全连接神经网络而言,卷积神经网络进步的地方是引入了卷积层结构和池化层结构,这两种层结构是CNN重要的组成部分。本章首先介绍卷积神经网络的基本结构,然后用一个例子解释对卷积和池化的通俗理解。接着,从更严格的角度介绍卷积的概念、原理与实现、分类和相关性质。最后,给出池化的概念、原理与实现和分类。学习完本章内容,读者将对卷积神经网络有初步的了解。
4.1 卷积神经网络的基本结构
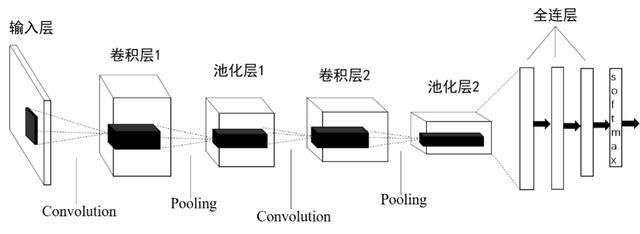
卷积神经网络又称卷积网络(Convolutional Networks),是在图像处理和计算机视觉领域应用较为广泛的一种神经网络。相对于全连接神经网络而言,卷积神经网络进步的地方是引入了卷积层结构和池化层结构,这两种层结构是CNN重要的组成部分。一个比较简单且用于图像分类问题的卷积神经网络结构如图4.1所示。
图4.1 卷积神经网络结构示意图
由于卷积神经网络各层中的神经元包含“深度”的概念,因而在图4.1中,每一层的单元都被组织成了一个三维立体矩阵(高度、宽度和深度)的形式。图4.1中的虚线部分展示了卷积神经网络内部连接情况。从图4.1可以看出,一个卷积神经网络主要包含5个层:输入层、卷积层、池化层、全连接层和softmax层。
(1)输入层。代表整个卷积神经网络的输入。例如,在图像分类问题中,输入是图像的像素矩阵。由前面的知识可知,如果是黑白图像,则深度为1(因为只有1个通道);如果是彩色图像,则深度为3(因为有R、G、B,3个通道)。
(2)卷积层。图4.1包含两个卷积层,卷积层实现对上一层输入的变换操作,会用到激活函数。卷积层的作用是获得更多图像的抽象特征。
(3)池化层。能够在宽度和高度方向上缩小上一层矩阵的大小,但深度并不会比上一层更深。此外,池化层能达到减少网络中参数的目的。
(4)全连接层。图4.1在卷积和池化之后构建了3个全连接层,卷积和池化可以看成是图像特征提取的结果,而全连接层的建立则是为后续分类任务做准备。
(5)Softmax层。通过该层可以得到输入样例所属种类的概率分布情况。
4.2 卷积与池化的通俗理解
卷积神经网络中有两个非常重要的层,分别是卷积层和池化层。那么,到底什么是“卷积”,什么是“池化”?下面以一个简单直观的例子说明,注意这个例子只能帮助我们直观地理解卷积与池化,但不属于严谨的定义。
4.2.1 对卷积的理解
假设现在有一张身份证,如图4.2所示,我们需要知道身份证是属于熊大,还是熊二、熊三、熊四。这时,我们需要解决的问题是识别身份证上是否出现了熊大的照片,人的肉眼很容易分辨这张照片的身份是谁的,但是计算机就没那么容易了。
图4.2 卷积与池化的直观示例
计算机相比于人来说,解决这个问题的方法更加机械化,具体过程如下。
(1)首先需要一张被转换为像素矩阵的熊大照片,该照片记录了熊大的图像特征。这张图像的像素矩阵称为“卷积核”。
(2)计算机会用这个“卷积核”(即熊大图像的特征)扫描身份证这个大图像,寻找是否有某个位置出现熊大的特征。
(3)卷积核与身份证上某个位置的图像特征进行相似度计算,这个计算就是“卷积”。如果计算的结果非常大,如0.99,就可以认为这个位置的照片很大程度上符合熊大的照片特征;如果计算的结果很小,如0.02,就可以认为在这个位置不太可能出现熊大的图像。
4.2.2 对池化的理解
如果利用卷积核在身份证这个大图像的整个平面上扫描,且没有出现特别强的相似性,则说明身份证上没有熊大的照片出现。熊大图像是否出现在身份证上,只依赖于计算出的相似特征的最大值,即只需要有一个局部图像与熊大照片非常相像,就可以认为身份证上出现了熊大头像。如果最大值不够大,则认为身份证图像中没有出现过熊大的照片。因此,在卷积核在图像上不断扫描的过程中,我们只关心卷积计算结果的最大值,这个最大化的操作,就是一种特殊池化方法,被称为最大池化(Max-Pooling)。
简言之,卷积就是计算某种局部的相似性,而池化就是将某种最突出的相似性选择出来。本章以下内容将从更严谨的角度对“卷积”与“池化”进行定义。
4.3 卷积
卷积层中的“卷积”(Convolutional)一词,说明网络结构使用了卷积操作,卷积是一种特殊的线性运算,用来代替一般的矩阵乘法运算。在图像处理中,针对图像的像素矩阵,卷积就是用一个卷积核来逐行逐列地扫描像素矩阵,并与像素矩阵中的元素相乘,由此得到新的像素矩阵,这个过程称为卷积。以图4.3为例,将一张图像简化为只有1个通道的5x5矩阵(即输入是5x5x1),使用的卷积核是图4.3中3x3的灰色矩阵。
图4.3 卷积计算示例
卷积操作就是将3x3卷积核从上到下逐行逐列扫描5x5的图像,每扫描一次,卷积核就与相应位置的图像数值进行线性组合。这样计算出的结果就形成了一个新的图像特征,称为输出特征图(Output Feature Map),是一个3x3的矩阵,如图4.3右侧所示的矩阵。该输出特征图仍然是一个3D张量,具有宽度和高度,其中深度可以是任意值,取决于使用了多少个卷积核,此时深度轴不再代表特定颜色。
如果上述例子使用了10个3x3大小的卷积核,那么输出特征图为3x3x10,说明对于这10个通道,每个通道都包含一个3x3的矩阵,这是卷积核对输入的响应图 (Response Map),表示卷积核在输入不同位置的响应。
因此,卷积运算由以下两个关键参数定义:
(1)卷积核的大小:通常是3x3或5x5,本例中为3x3。
(2)输出特征图的深度:由使用的卷积核的数量决定,本例中为10。
上面所举的例子将一个5x5的图像矩阵变为了3x3的矩阵,这种变换并不是唯一的,只是一种特殊的卷积方式,不同方法的卷积计算产生的矩阵大小是不相同的。下面一一讨论这些方法。
4.3.1 卷积运算原理
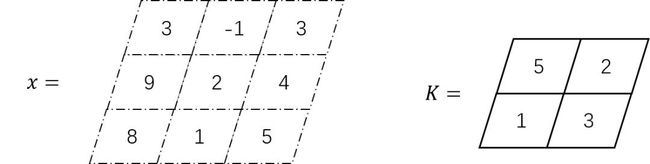
卷积运算共有3种类型:full卷积、same卷积和valid卷积。下面以3行3列的二维张量X和2行2列的二维张量K的卷积进行介绍,其中K又称为卷积核或滤波器,如图4.4所示。
图4.4 二维张量与二维卷积核
01 full卷积
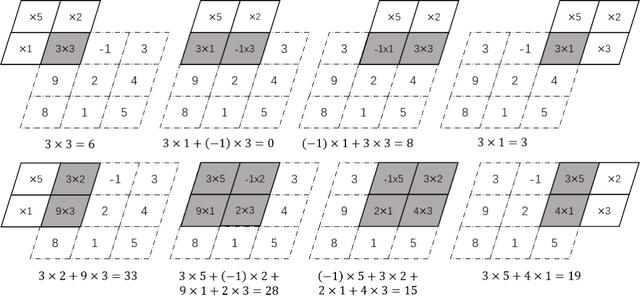
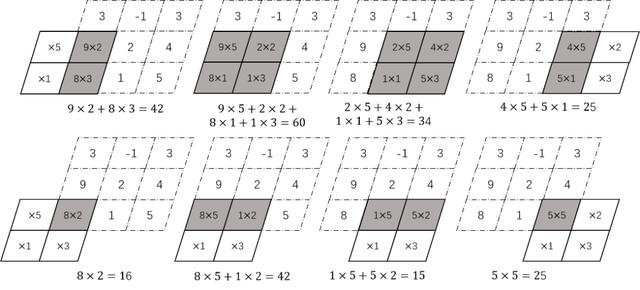
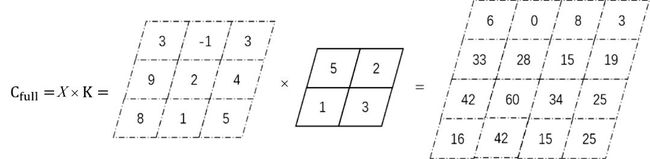
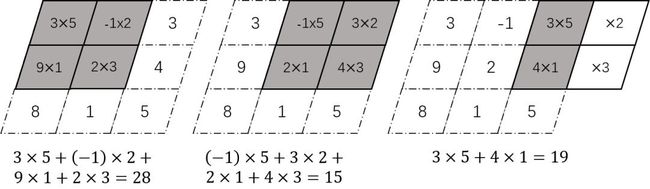
full卷积的计算过程为:K沿着X按照先行后列的顺序移动,每移动到一个固定位置,对应位置的值相乘,然后求和。full是完全的意思,即只要像素矩阵与卷积核元素有一个位置重叠,就要计算,并将落在像素矩阵外的元素全部视为0。具体过程如图4.5所示。
图4.5 full卷积的过程
最后将得到的值依次存入
中,得到图4.6所示的结果,是一个4×4的矩阵。
图4.6 full卷积的结果
这种卷积类型在实际应用当中有什么意义是未知的,它可能对有些数据有效,对有些数据无效。但是,full卷积作为一种卷积的基础类型,是需要大家了解并掌握的。
02 same卷积
same卷积是在实际应用中十分常见的卷积类型。same的含义是卷积前后像素矩阵保持同样维度。将X与K进行same卷积,首先需要为K指定一个起始点,然后将起始点按照先行后列的顺序移动到X的每一个位置处,对应位置的值相乘然后求和。假设卷积核K的高等于H,宽等于W,则起始点的位置可以由下表4.1的规则获得。
表4.1 确定起始点位置的规则表
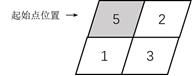
如之前的例子,卷积核K的高为2,宽也为2,因此起始点的位置为(0,0),如图4.7所示。
图4.7 起始点的位置
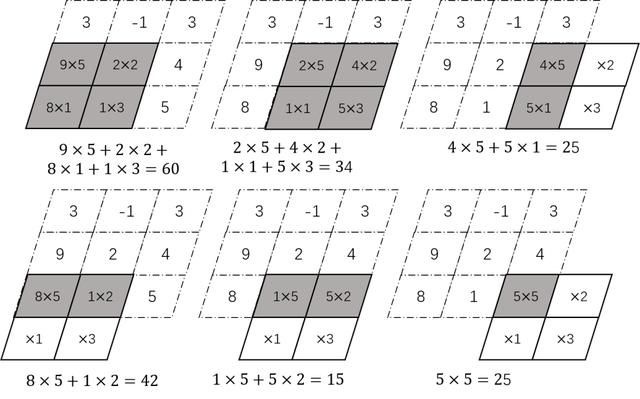
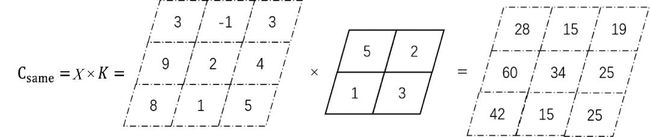
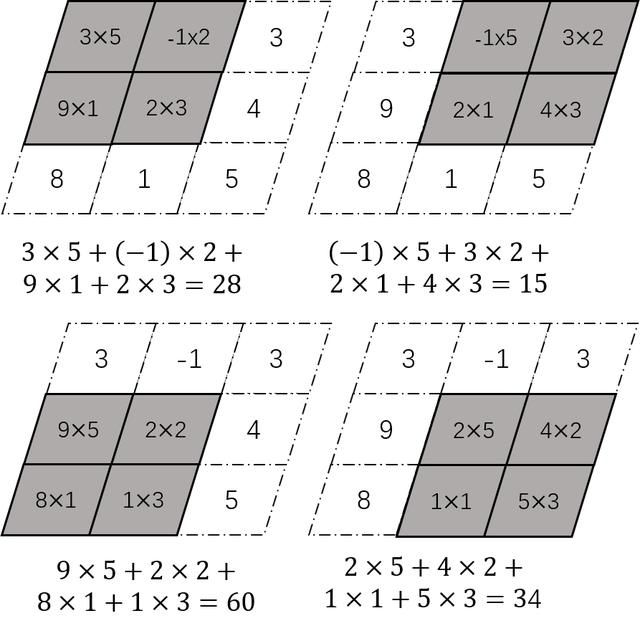
same卷积的具体计算过程如图4.8所示。将卷积后得到的值依次放入
中,得到如图4.9所示的结果,为一个3×3的矩阵,可以看到最后的卷积结果和原始张量具有相同的维度。
图4.8 same卷积的计算过程
图4.9 same卷积的结果
03 valid卷积
无论是full卷积还是same卷积,可以看到,都会有卷积核K有部分延伸到X以外的情况发生,此时延伸的部分需要用0来填充之后才能进行计算。本小节介绍另外一种卷积方式,即valid卷积,它只考虑X能完全被K覆盖的情况(即K在X内移动)。valid卷积要求卷积核完完全被覆盖在像素矩阵的有效范围之内。仍以图4.4所示的二维张量和二位卷积核为例,valid卷积的具体计算过程如图4.10。
图4.10 valid卷积的计算过程
将得到的值依次存入
中,结果为一个2×2的矩阵,如图4.11所示。
图4.11 valid卷积的结果
经过valid卷积后,矩阵的维度变小了,这种类型的卷积似乎在数学上更为合理,但也带来了问题:矩阵维度发生了变化。维度变化的规律会随着像素矩阵与卷积核大小的不同而不同。因为矩阵维度的变化会影响到之后的计算,所以使用valid卷积需要十分小心,并时刻注意矩阵维度的变化。
好了,第四章的第一部分内容今天就更新完毕了,下周继续更新第四章剩余的内容,欢迎大家同步收看狗熊会慕课平台的深度学习课程,里面有熊大的精彩讲解!