2022年数维杯数学建模C题 电动汽车充电站的部署优化策略求解全过程文档及程序

2022年数维杯数学建模

C题 电动汽车充电站的部署优化策略

原题再现：

  近年来，随着化石能源的逐渐枯竭和环境污染的不断加剧，电动汽车（EV）作为传统燃油车的主要替代品之一，得到了快速的发展。据国际能源署统计，2019年全球电动私家车已达 7.2 百万辆，较 2018 年增长了 40% 。EV 公共充电设施为 EV 提供充电续航服务，也得到了快速发展。然而由于没有合理的统筹，公共充电设施存在利用率低、寻桩困难、充电等待时间长等问题，造成了土地、财政补贴、电力等资源的极大错配与浪费，大大降低了社会综合效益。本赛题旨在通过数学建模，为城市内公共充电站的选址和定容提供优化部署方案，提高社会综合效益。
  由于充电站的建设与运营涉及多个利益主体，主要包括充电站建设运营商（简称充电站），EV 用户和电网等 。各个利益主体的利益并不一致，例如，如果充电站加大投入，EV 用户将获得更高质量的充电服务，但充电站可能由于过高的充电设施闲置率和运维成本造成收益下降；反之，EV 用户将得不到可靠的充电服务，例如充电设施数量不足或距离过远，排队等待时间过长等。而电网方面主要考虑的是能源的整体利用效率和配电网络安全等。
  EV 充电站部署的主要依据是 EV 用户充电需求的时空分布，充电需求的时空分布受到 EV 规模、出行行为和充电行为等因素的影响。一般来说，车流量大的地方充电需求旺盛，反之则充电需求较少。同时，城市功能区也会影响 EV 用户的充电行为，例如，EV 用户更倾向于选择饭店、超市、停车场等需要滞留的场所进行充电。由于大数据技术的兴起，数据驱动作为研究实际问题的方法之一被广泛采用 [3,4]。本赛题主要提供两个相关数据集，介绍如下：
  数据一：北京出租车轨迹数据（txt 格式），其包含了 10357 条北京出租车GPS 轨迹数据，时间段为 2018 年 2 月 2 号至 2 月 8 号。数据具体格式见 Table 1，具体数据见附件一，详细说明见附件三。

  数据二：北京路网数据，该数据是从 OpenStreetMap 网站下载北京路网数据并由Python 模块 osm2gmns 提取得到。包含三个数据表（csv 格式），node，link 和
poi，分别记录了道路交叉口信息，道路信息和兴趣点信息。具体数据见附件二。
  OpenStreetMap 网站：https://www.openstreetmap.org/
  三个数据表说明详见：
  https://osm2gmns.readthedocs.io/en/latest/gmns.html
  通过数据一和数据二，可以构造出北京的真实路网和出租车的出行信息。参赛者可以自行选取所需数据，赛题之外的数据也被推荐使用，但需要注明出处。（需要注意的是，赛题提供的数据均处于 WGS 84 坐标系下）。
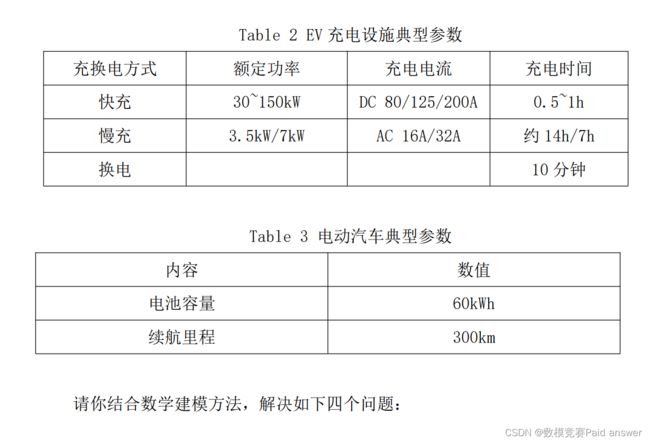
  为了研究方便，赛题给出 EV 充电设施和 EV 的典型参数（仅供参考,参赛者可根据建模需要自行调整），分别如 Table 2, Table 3 所示

  问题一：请你结合数据一和数据二，确定在当前的出租车数量规模下（假设所有出租车均是电动汽车）的最优充电桩位置及其数量分布结果。
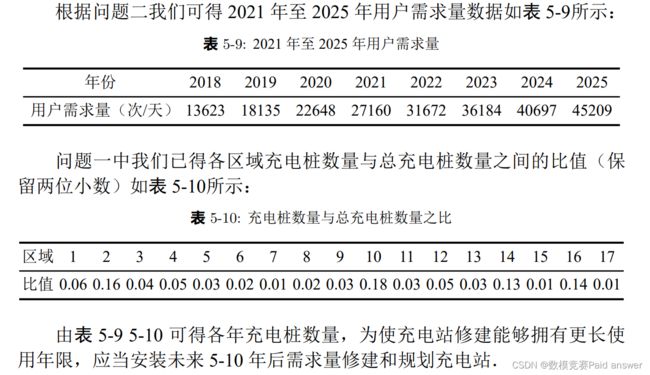
  问题二：请根据赛题所提供的数据及你能够搜集整理到的相关数据，预测北京市 2021 至 2025 年的 EV 用户充电需求的时空分布。（预测结果可以通过图或表格的形式进行展示）
  问题三：基于问题二得到的充电需求时空分布，在问题一的基础上进一步提出充电桩的逐步扩充或减少的量化模型，并给出规划区域和时段内 EV 公共充电站的运营时间表。（最好将相关结果以可视化方式展示出来）。
  问题四：在极端寒冷天气下，电动汽车的电量消耗会快速上升，这会使得充电桩的短时间充电需求过高，您能否根据问题二中的预测数据提供极端寒冷天气下的同时考虑充电和换电的最优方案？（换电是指直接更换同类型电池）
  附件：
  附件一：北京路网数据集
  附件二：充电桩数据
  附件三：充电桩数据集说明

整体求解过程概述(摘要)

  新能源汽车是全球汽车产业绿色发展和转型升级的重要方向，也是我国汽车产业发展的一种战略选择．大力推进充电基础设施建设，有利于解决电动汽车充电难题，是新能源汽车产业发展的重要保障．本文解决了以下问题：
  对于问题一：根据所给数据集确定最优的充电桩位置及数量分布，本文首先收集了北京 2018 年 2 月 2 日-8 日电动车共 10357 辆出租车的 GP S 轨迹数据，其次考虑定义为需求点的条件，最终确定间隔时间大于等于 30h 且速度小于 1KM/h，确定共有 95362 个需求点，进而建立基于距离的 K−Means 聚类模型，共将其聚为 17 类，需求点最多的 3 个类别其聚类中心坐标为（116.4821，39.95636）、（116.4235,39.86061）、（116.3103,39.89656），需求点个数分别为 16739,15428,13053．进而对 17 个类别继续聚类，最终得到最优的充电桩数量总计为 31397 个，详细结果如图 5-8．
  对于问题二：需要预测北京市 2021-2025 年的 EV 用户充电需求的时空分布，本文首先在中国充电联盟爬取了数据，通过分析 pearson 相关系数可知，与北京公共充电桩数量相关程度最大的为新能源汽车保有量，其相关系数为 0.9923，因此通过预测新能源汽车保有量来预测用户需求的时空分布，新能源汽车保有量随时间的拟合回归方程为y1 = 102.82x−207215 ，拟合优度 R2 为 0.9891，北京公共充电桩数量 y2 = 134.8y1+3562.9，拟合优度 R2 为 0.9653，通过 2018 年需求量与北京公共充电桩数量比值 3.0373, 进而预测出需求分布的时空分布，类别最多的 3 类结果如表 5-8所示.
  对于问题三：本文通过区域充电桩数量与总充电桩数量之比与问题二得到的用户需求时空分布数据确认充电桩数量，如 2023 年的充电桩需求量 36184，得出充电桩总数量108552，通过区域七对应的比值 0.01 得出 2023 年区域 7 的充电桩数量为 1085，较 2022年区域七数量 950 增加了 14.2%，通过该数值可逐步对充电桩进行扩充．并对充电数据，我们划分为高校、工作区和研究区三个充电区域，统计所有区域不同时间段充电数量得出 5 点到 13 点是充电高峰期，峰值出现在 7 点左右，在这个时段我们可开放更多充电桩；统计所有区域周末和工作日充电数量得出工作日充电量占总数 91%，周末只有 9%，我们可在周末减少充电桩运营时间以降低运营成本．
  对于问题四：本文通过站点各月的总充电时长和总充电量统计，得出 10 月至 2 月较其他月份真实充电量增加约 31.48%，故应更改充电站充换点方案以满足用户需求．

问题分析：

  题目数据集包含来自加州理工大学的三个充电站充电桩数据、北京路网数据，其中包含：道路交叉口信息、道路信息、景点信息．根据北京出租车轨迹数据以及北京路网数据，以这部分数据得到用户轨迹信息并得到用户的时空分布，分析其充电需求给出最优的充电桩位置及数量．由于极端寒冷天气、大型国际活动、节假日出行等多个方面都可能对充电桩需求带来影响，考虑这些因素的影响并给出最优方案．
  对问题 1 研究的意义的分析．问题 1 需要根据题目所提到的北京出租车轨迹数据对充电桩位置及数量进行规划，对于解决此问题，我们首先分析建立一个充电站的需求是从何而来，题目所提到出租车司机用户存在充电需求一般分为三个方面：1. 车辆电量达到阈值；2. 换班或下班；3. 三餐期间；我们将一个用户可能存在充电需求的经纬度坐标定义为一个需求点．其次需要考虑到尽可能多的需求点．根据北京出租车轨迹数据停留时间长短及坐标变化确定需求点，将需求点数据进行多次聚类，首先得到大区域，再将各区域划分为小区域并得到充电桩数量．
  对问题 2 研究的意义的分析．问题 2 要求根据题目所给数据或收集的
数据对北京未来几年用户充电需求的时空分布进行预测，我们需要获得此前用户充电需求的趋势变化，根据趋势变化对未来进行预测．由于题目所给数据量较小，故需要对各年北京市 EV 用户数量数据进行收集，并考虑国际能源价格趋势、国内政策扶持、用户对新能源车型的评价等多个方面对
充电需求的影响，最终根据问题一所得时空分布，得到结果：北京市 2021至 2025 年的 EV 用户充电需求的时空分布．
  对问题 3 研究的意义的分析．问题 2 中我们已得未来北京市充电需求时空分布，由于未来新能源车的发展，其充电需求与第一问数据相较有所变化，而我们所规划的充电桩位置及数量应在未来几年甚至几十年都能有效利用，故需要根据问题 2 所得“北京未来几年用户充电需求的时空分布”情况将问题 1 规划结果进行修正，并根据各区域用户习惯、出行规律等条件，规划出区域充电站的运营时间表．
  对问题 4 研究的意义的分析．在前面三个问题中，均根据用户自身的
需求对充电桩位置及数量进行规划，在问题 4 中，加入了外来因素的影响，例如题目所说极端寒冷天气对汽车电量的影响，以及由于大型事件、节假日造成外来车辆激增，这些都会使充电桩的短时间充电需求过高，若根据短时间的需求增加充电桩的数量，则会增加充电站运营成本．故我们需要根据外来因素影响所造成的需求量变化再次规划充电桩的位置及数量、充电桩的类型、以及换电站的设置．在附件一中，我们可以得到三个充电站接近三年的充电数据，根据这部分数据可以分析用户充电习惯、车辆充电类型分布等多方面数据．

模型假设：

  1. 假设数据集中出租车均为同质纯电动车；
  2. 假设题目所给电动汽车典型参数为出租车实际参数；
  3. 出租车司机会选择可接受范围内较近的充电站进行充电；
  4. 任何充电站的任何一个充电桩都只能为一辆电动汽车服务；

模型的建立与求解

  数据的获取与预处理：
  1. 根据题目描述信息，我们需要利用北京出租车轨迹、北京路网数据对北京出租车用户充电需求的时空分布进行分析，并给出充电桩位置及数量的分布．故我们通过微软 T-Drive trajectory data sample 项目得到包含 2008年 10357 辆出租车的一周轨迹信息样本数据．该数据集点的总数约为 1700万条，轨迹总距离达到900万公里以上．
  2. 　北京出租车数据集为10357 个txt 文件，分别代表 10357 辆出租车其七天位置变化信息．首先我们将 txt 文件进行合并，得到合并数据集taxi.csv，由于数据量达 970MB，故附件中不给出原始数据集，仅提供数据处理代码．
  3. 合并数据集格式如表5-2：

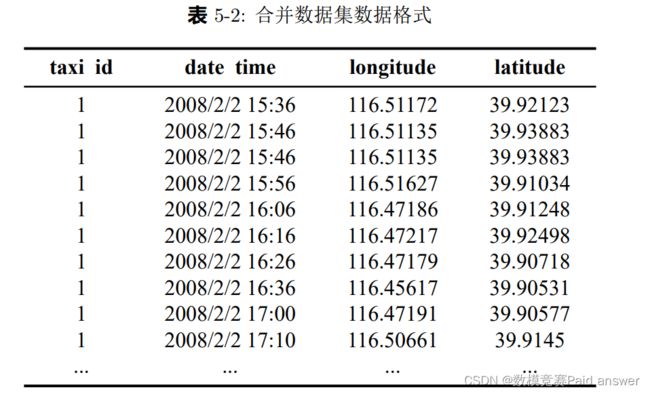
  第一列为出租车 id，唯一对应一辆出租车，第二列为时间，第三、四列表示当前时间车辆所处经纬度坐标．由 taxi id 列可知有 21 辆出租车数据不存在，数据集实际为 10336 辆出租车数据，date time 列由于题目将时间设定为 2018 年，故在问题二中将此数据类比为 2018 年对应数据．最后利用经纬度绘制散点图如图5-1所示：

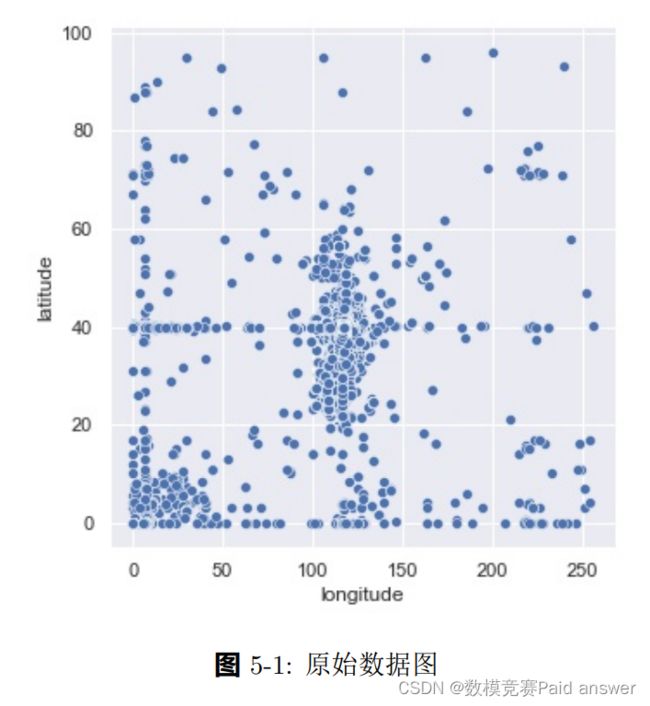
  由图 5-1可以看出出租车位置信息分布及其不合理，由于数据集来自北京出租车轨迹信息，其坐标位置应处于北京及其周边地区．选取图中左下角数据点进行分析，其经纬度 ( 0◦, 0◦) 在地图上位于非洲几内亚湾．为真实数据可能性极小，故通过北京其真实经纬度数据对数据集中不合理数据进行删除，最终得到处理后的数据集．
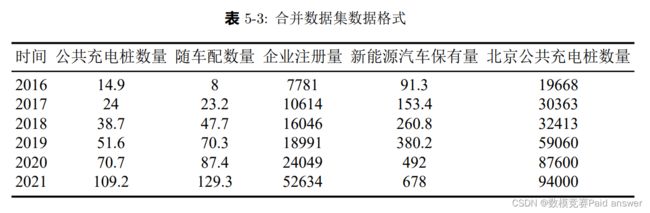
  4. 除出租车轨迹数据外，问题二需要我们对 2021 至 2025 年的电动汽车充电需求的时空分布进行预测，但目前我们仅有 7 天出租车轨迹数据、北京路网数据、加州充电桩数据，仅根据已有数据集预测未来数据准确率极低，故我们收集部分数据如表 5-3所示：

  模型的建立与求解：
  “类”表示一个具有相似性的数据集合，“聚类”即是将可能存在相似的数据集划分为多个“类”，使得各个“类”之间相似性尽量小．故聚类分析又称为群分析，是对多个样本（或指标）进行定量分类的一种多元统计分析方法．本文所使用的是根据样本进行分类的 K − Means 算法．

  题目所给数据为不同时间出租车对应经纬度坐标，若用户对附近充电站进行选择，较大概率会选择距离最近的充电站．而 K − Means 算法正是基于欧式距离来度量样本之间的相似程度．其聚类类别中一条数据距离当前类别聚类中心相对更近，故可将聚类中心作为充电站修建候选点之一．度量样本间的相似性时常用欧几里得距离计算公式如式1：

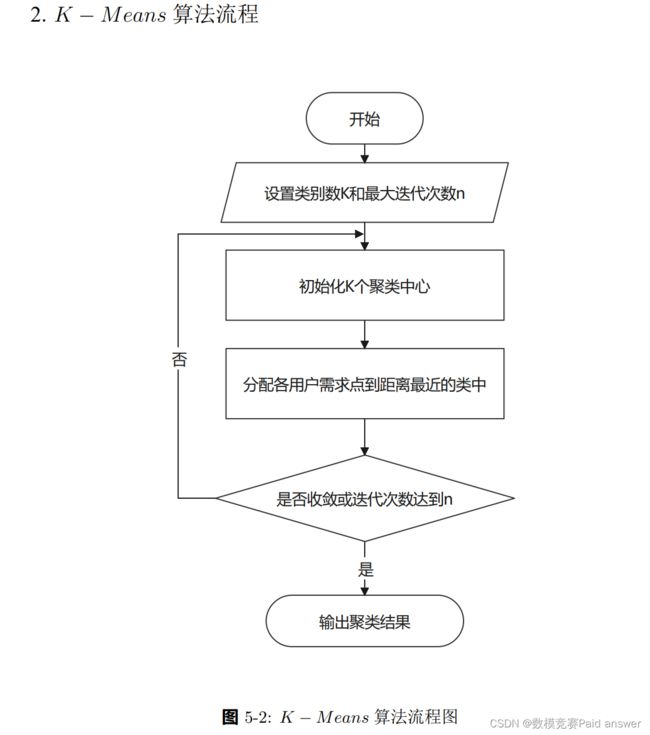
基于 K − Means 算法模型的求解

  由于 K − Means 基于欧式距离划分类别，均值和方差过大将对聚类产生决定性影响．故在对数据点进行聚类前首先需要进行标准化处理．除此之外，离群点、异常值对均值产生较大影响，导致中心偏移．在开始问题一之前我们已对数据进行初步处理，去除部分异常值．
  需求点的构建：
  北京出租车轨迹数据中为多辆车 7 天的轨迹数据，取 taxi id为5555 的数据进行数据探索性分析：

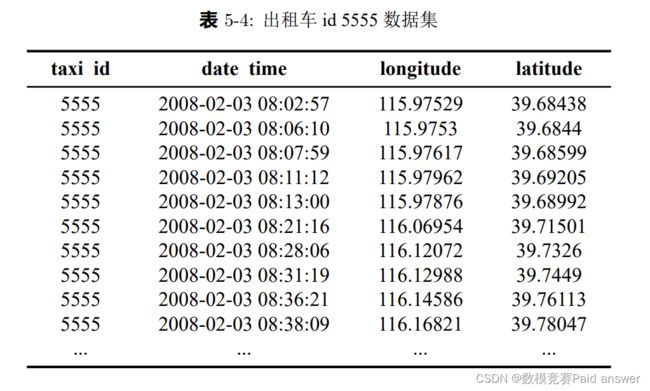
  表中数据其时间列均以 5 分钟为间隔，且经纬度坐标始终处于变换状态，则我们可合理认为当前出租车处于运动状态，当出租车处于运动状态，则说明当前司机处于载客、出行等情况，则不会产生充电需求．根据题目所给电动汽车快充其充电时间约为 0.5 − 1h，当司机静止时间超过 0.5 小时，则可能存在充电意愿（即使当前车辆电量较为充裕），通过绘图查看车辆GPS定位数据时间间隔频次如 图 5-3 所示：

  由图 5-3 可知间隔分布主要分布在 30 分钟以下、6 小时和 10 小时，大量数据分布于 6、10 小时，通过查阅北京出租车运营情况，我们认为在这两个时间段为换班场景或休息场景，也存在充电需求．其次通过经纬度的变化可以计算出在当前时间间隔中车辆移动距离，本文采用Haversin公式进行计算，如式3：

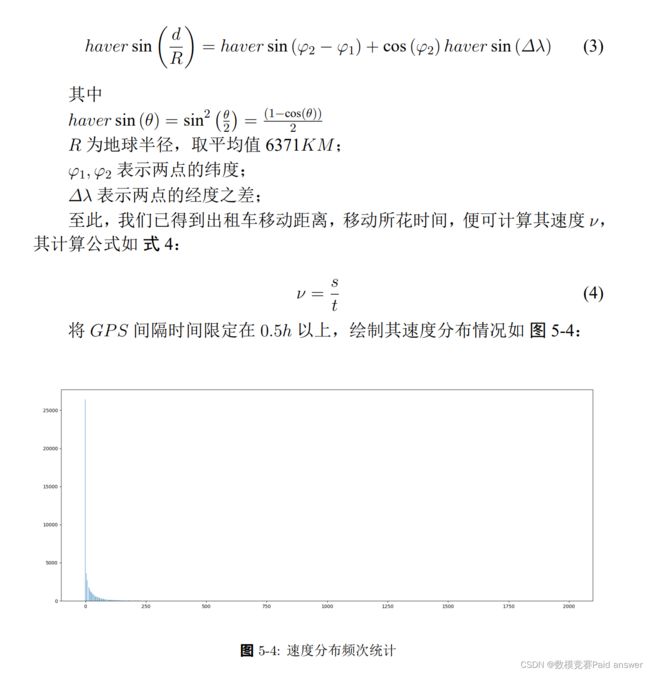
  由图像可得速度数据其拖尾极长，极值数据量极少，速度为0-0.025KM/h范围内数据存在 26400 条，而速度最大为 49.90KM/h．若出租车保持 30 分钟以上时速为 49.90KM，则该出租车应处于正常行驶状态．最终我们选取所有下一条 GP S 记录距离本次超过 0.5h 且通过两条数据计算其速度小于 1KM/h，则我们认为其处于静止状态，由于其静止时间超过 0.5h，则将当前经纬度记录为一个需求点，最终取得需求点个数为:95362个．其分布情况如图5-5：

  对 95362 个聚类分析得到其聚类中心，由于 K − Means 算法其 K 值的选取对聚类结果影响很大，本文采用手肘法确定 K 值，如 图 5-6：

  由图 5-5可以看出，当 K 为 17 时，其斜率达到最大值，通过手肘法我们认为 17 为 K 的最佳值．利用所得 K 值对 95362 个需求点进行聚类分析，得到聚类结果如图5-7：


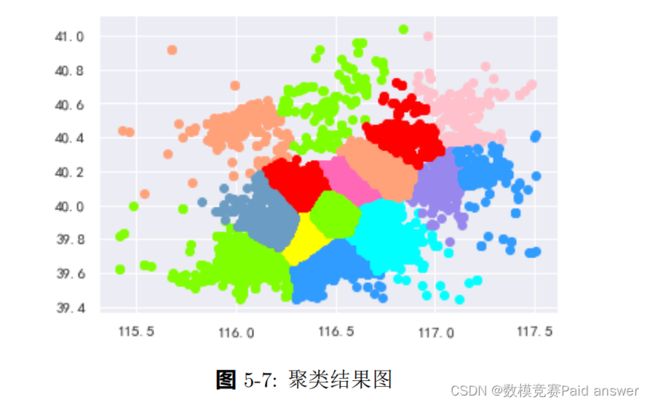
  根据北京出租车轨迹数据及其数量规模条件，并假设所有出租车均为电动汽车，本文通过数据分析处理得到车辆停留点，将车辆停留点定义为用户需求点．根据用户需求点进行聚类分析得到不同区域及区域内需求点数量，根据其需求点数量可得各类别数量中充电桩数量如表 5-6：

  充电桩具体位置选择应考虑多方面因素，首先充电桩的设立应满足用户出行需求，如两个充电桩安装区域之间距离应在可接受范围内才能满足用户充电需求；其次充电站由于提供充换电服务时容易引发火灾等安全隐患，因此充电站在建设时需要与周边环境保持安全距离，例如远离学校、医院等人员密集场所；居民区可在小区停车场安装充电桩而不是修建充电站，换电站可修建在高速路出口处等．
  通过再次聚类得到二次聚类结果如 图 5-8：

  前期我们对相关数据进行收集整理如 表 5-3所示，利用这部分数据对未来北京 EV 用户充电需求时空分布进行预测．其相关性分析结果如下：

  由图像我们可得，北京公共充电桩数量与新能源汽车保有量呈高度相关性，其相关性系数为 0.9923，如图 5-10所示：

  当两变量呈高度正相关时，我们便可以通过已知变量对未知变量进行预测，而北京公共充电桩数量一定程度上与真实用户需求也应呈高度正相关．故我们希望再次利用北京公共充电桩数量对未来北京公共充电桩数量进行预测．通过北京充电桩数据与用户需求量之间的关系进行对应，从而达到预测 2021 年至 2025 年充电需求的目的．
  建立回归模型得到线性回归方程：

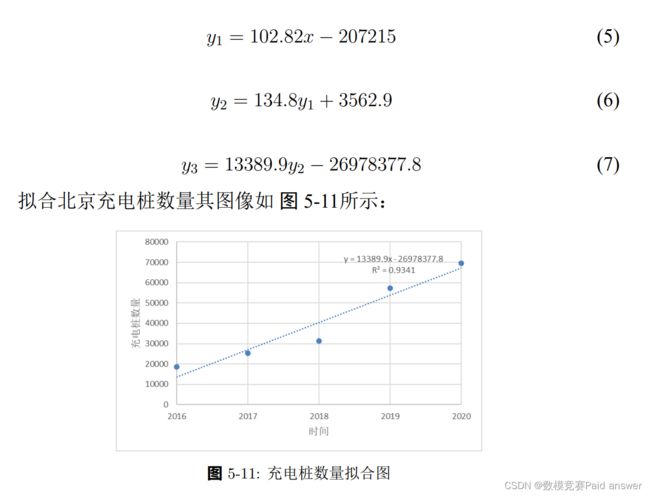
  回归模型检验：
  通过 SPSS 输出的回归模型总结表中，R 表示回归系数（即相关系数值），R 表示判定系数，即回归系数的平方．判定系数显示了预测的准确度提高了多少，其对比的基准点是用平均值作为预测得出的误差的平方和．R，也称拟合优度，表示拟合得到的模型能解释因变量变化的比例．最佳拟合线只有在完全相关（R=1 或者-1）时才能提供准确的预测．R=1 时，意味着变量 100% 的变化可以由最佳拟合线解释．在这种特殊情况下，如果样本数据能够真实表达总体，预测就会完全准确．
  方差分析主要作用是通过 F 检验来判断回归模型的回归效果，即检验
因变量与所有自变量之间的线性关系是否显著，用线性模型来描述它们之间的关系是否恰当．如果没有线性关系，那么各偏回归系数均为零．回归系数的显著性检验主要看 t 值和显著性（P 值）两个指标．其检测结果如下：

  由表可知 P 值小于 0.05，因此具有显著性，可用于拟合回归方程，且R2 为 0.934，拟合优度良好，则可利用 2018 年需求量与北京公共充电桩数量其比值, 进而预测出需求分布的时空分布．

对问题的求解

  首先我们可以利用模型预测出 2021 年至 2025 年北京市公共充电桩数量，根据“2018 年”EV 用户充电需求点数据可得用户充电需求量，根据用户充电需求量与北京市公共充电桩数量之比，预测出 2021 年至 2025 年用户充电需求量．


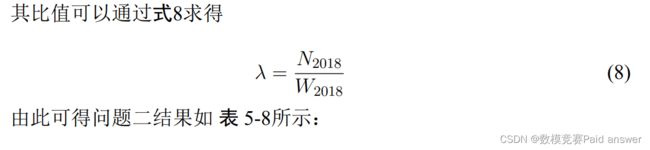
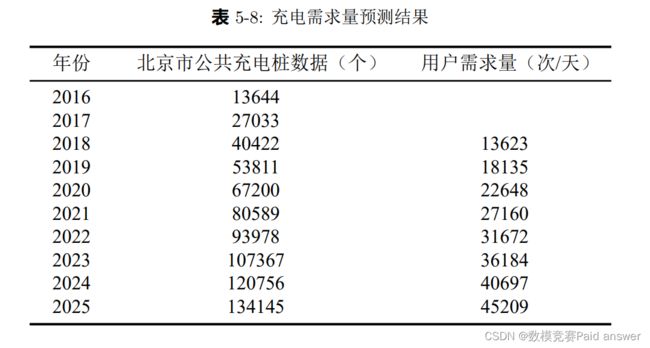
  问题三要求我们根据问题二中所得结果：未来“充电需求时空分布”，在问题一的基础上对充电桩数量进行扩充和减少，并规划区域中不同时段内公共充电站的运营时间表．

规划区域：

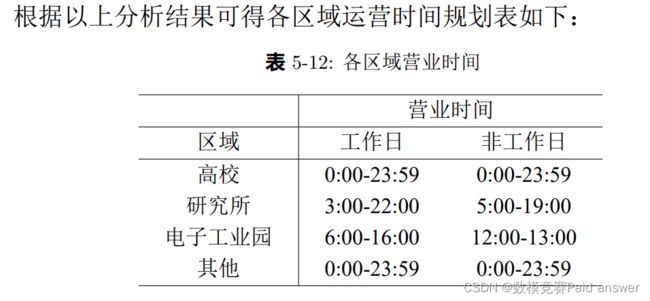
  由于我们需要对区域其充电站的运营时间进行规划，首先需要选取部分区域进行规划，例如本文中选取三个地区作为代表区域，并根据其充电数据规划合理运营时间．题目所给数据为加州三个充电站（加州理工、jpl 实验室、硅谷办公室）充电数据，因为研究对象均为电动汽车用户，可以类比为其相似类型区域，其对应区域类型为（高校、研究所、电子公业园）．

对问题的求解

规划运营时间表：

  首先我们对数据集进行探索性分析，数据包含车辆开始充电时间、结束充电时间、停留时间、实际充电时间及电量、星期几和站点地址，通过数据我们可以根据用户充电规律得到有用信息．
  首先我们按地点将数据集划分为三个充电站点数据集，并分别分析其充电在全天各时间段频率分布，并根据结果得到对应运营时间．

  高校区域图像可看出其充电需求高峰位于早上 8 点以及晚上 6 点，非工作日于早上 10 点也存在充电需求增多的情况，用户更愿意在工作、学习时间为车辆充电．
  相较于其他区域，高校区域人群于 0 点需求量更高，由于高校区域人员组成更趋于年轻化，作息时间更为不规律，故在设置运营时间时，我们应考虑当前区域人员组成情况，更好的为用户服务．
  研究所区域：

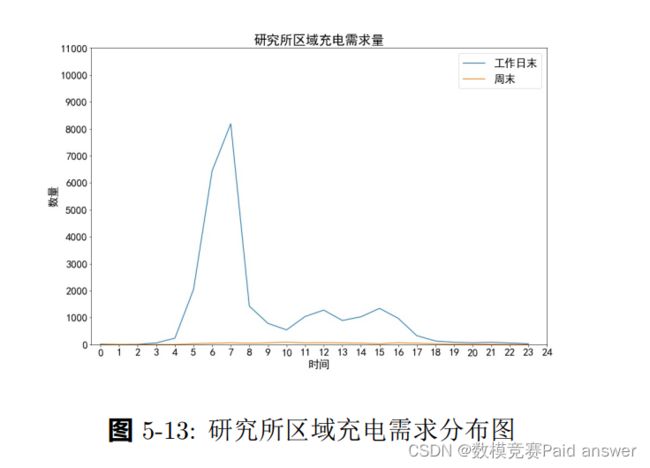
  研究所区域其图像与高校相似，但数据量相较更大，可说明研究所区域电动汽车使用人数相较更多，研究所区域早高峰相较更早，且早高峰后曲线下降更明显，工作人群时间相对更为紧张．

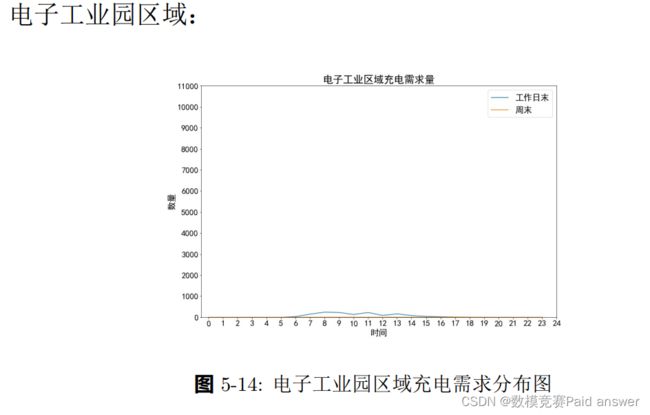
  电子公业园区域电动汽车使用量较小，曲线相较更为平滑其高峰时间段为 8-9 点．

  问题四要求我们对温度降低造成电动汽车里程减少的情况进行分析，并给出充换电解决方案，按月对充电桩数据集进行统计，可得到各月充电时长及充电量分布情况，如图 5-15

  由图像可看出全年充电量峰值在 10 月至次年 2 月，其对应季节为秋冬两季，秋冬两季气温下降导致车辆续航里程减少，充电需求增加，通过数据统计其充电量相较其他月份增加约 31.48%，故我们对充电桩进行规划过程中应考虑到因温度下降导致的需求量增加．除温度影响外，北京作为国际交往中心，大型活动举办也会造成充电量的增加，在目前充换电方案中，“换电”速度最快，仅需要 10 分钟，但换电站其工作原理为为用户更换充满的电池，故更换下的电池需要在充电站中进行充电，目前常用充电桩其最大更换电池个数为 30，若需求车辆超过30，则只能使用快充以提高效率．

论文缩略图：

程序代码：

import warnings
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib . pyplot as plt
import datetime
import matplotlib . font_manager as fm
from statsmodels . graphics . api import qqplot
from datetime import datetime
plt . rcParams ['font .sans - serif '] = ['SimHei '] # 中文字体设置 - 黑体
plt . rcParams ['axes . unicode_minus '] = False # 解 决 保 存 图 像 是 负 号 '-' 显 示 为 方 块 的 问 题 # 解决 Seaborn 中 文 显 示 问 题
sns . set ( font ='SimHei ', font_scale =1) # 解决 Seaborn 中 文 显 示 问 题
fig = plt . figure ()
warnings . filterwarnings (" ignore ")
# 读取 数 据表
df1 = pd . read_excel (r'juleidata . xlsx ')

julei_data = df1 . iloc [: ,2:4]
np . array ( julei_data )
import numpy as np
import matplotlib . pyplot as plt
# 两点距离
def distance ( e1 , e2 ):
return np . sqrt (( e1 [0] - e2 [0])**2+( e1 [1] - e2 [1])**2)
# 集合中心
def means ( arr ):
return np . array ([ np . mean ([ e [0] for e in arr ]) , np . mean ([ e [1] for e in arr ])])
# arr 中距离 a 最远 的元 素 ， 用 于 初 始 化 聚 类 中 心
def farthest ( k_arr , arr ):
f = [0 , 0]
max_d = 0
for e in arr :
d = 0
for i in range ( k_arr . __len__ ()):
d = d + np . sqrt ( distance ( k_arr [ i ] , e ))
if d > max_d :
max_d = d
f = e
return f
# arr 中距离 a 最近 的元 素 ， 用于聚类
def closest (a , arr ):
c = arr [1]
min_d = distance (a , arr [1])
arr = arr [1:]
for e in arr :
d = distance (a , e )
if d < min_d :
min_d = d
c = e
return c
if __name__ ==" __main__ ":
## 生 成 二 维 随 机 坐 标 ， 手 上 有 数 据 集 的 朋 友 注 意 ， 理解 arr 改 起 来 就 很 容 易 了
## arr 是一 个 数组 ， 每 个 元 素 都 是 一 个 二 元 组 ， 代 表 着 一 个 坐 标
## arr 形如 ：[ (x1 , y1), (x2 , y2) , (x3 , y3) ... ]
arr = np . array ( julei_data )
## 初 始 化 聚 类 中 心 和 聚 类 容 器
m = 17#l 类别数
r = np . random . randint ( arr . __len__ () - 1)
k_arr = np . array ([ arr [ r ]])
cla_arr = [[]]
for i in range (m -1):
k = farthest ( k_arr , arr )
k_arr = np . concatenate ([ k_arr , np . array ([ k ])])
cla_arr . append ([])
## 迭代聚类
n = 20
cla_temp = cla_arr
for i in range ( n ): # 迭代 n次
for e in arr : # 把 集 合 里 每 一 个 元 素 聚 到 最 近 的 类
ki = 0 # 假 定 距 离 第 一 个 中 心 最 近
min_d = distance (e , k_arr [ ki ])
for j in range (1 , k_arr . __len__ ()):
if distance (e , k_arr [ j ]) < min_d : # 找 到 更 近 的 聚 类 中 心
min_d = distance (e , k_arr [ j ])
ki = j
cla_temp [ ki ]. append ( e )
# 迭 代 更 新 聚 类 中 心
for k in range ( k_arr . __len__ ()):
if n - 1 == i :
break
k_arr [ k ] = means ( cla_temp [ k ])
cla_temp [ k ] = []
## 可视 化 展示
col = ['HotPink ', 'Chartreuse ', ' LightSalmon ', 'pink ', '#359 aff ', 'red ','Aqua ', 'Chartreuse ', 'yellow ', '#6 b9bc2 ',
'#9687 ed ','HotPink ', 'Chartreuse ', ' LightSalmon ', 'pink ', '#359 aff ', 'red ']
for i in range ( m ):
plt . scatter ( k_arr [ i ][0] , k_arr [ i ][1] , linewidth =10 , color = col [ i ])# 聚类 中心 点
plt . scatter ([ e [0] for e in cla_temp [ i ]] , [ e [1] for e in cla_temp [ i ]] , color = col [ i ])
plt . show ()
from sklearn . cluster import KMeans
kmeans = KMeans ( n_clusters =17 , random_state =123). fit ( julei_data )
# 简 答 打 印 结 果
r1 = pd . Series ( kmeans . labels_ ). value_counts ()
r2 = pd . DataFrame ( kmeans . cluster_centers_ )
r = pd . concat ([ r2 , r1 ] , axis =1)
r . columns = list ( julei_data . columns )+[ u' 类别数目 ']
print (r )
# 详 细 输 出 原 结 果
r_new = pd . concat ([ pd . DataFrame ( julei_data ) , pd . Series ( kmeans . labels_ )] , axis =1)
r_new . columns = list ( julei_data . columns )+[ u' 类别数目 ']
# 导包
# coding : utf8
import pandas as pd
import numpy as np
import matplotlib
import matplotlib . pyplot as plt
import sys
from matplotlib . ticker import MaxNLocator
from collections import namedtuple
from matplotlib . font_manager import FontProperties
import seaborn as sns
from matplotlib . pyplot import MultipleLocator
from datetime import datetime
font_set = FontProperties ( fname = r" *** path ***/ mpl - data / fonts / simfang . ttf ")
matplotlib . rcParams ['figure . figsize ']
matplotlib . rcParams ['savefig .dpi ']
plt . rcParams ['font .sans - serif '] = ['SimHei '] # 解 决 中 文 显 示 问 题
plt . rcParams ['axes . unicode_minus '] = False # 解 决 中 文 显 示 问 题
plt . figure ( figsize =(15 , 10))
plt . rcParams ['font . size '] = 20
from math import radians , cos , sin , asin , sqrt
# 问 题 一 文 件 读 取
data = pd . read_csv (r'taxi . csv ')
# 画 经 纬 度 分 布 图
sns . set ( style ='darkgrid ')
plt . figure ( figsize =(10 ,10))
sns . relplot ( x ='longitude ', y ='latitude ', data = data )
plt . show ()
# 删 除 北 京 之 外 的 经 纬 度
data = data . loc [ data ['longitude '] >=115.416827 ,:]
data = data . loc [ data ['longitude '] <=117.508251 ,:]
data = data . loc [ data ['latitude '] >=39.442078 ,:]
data = data . loc [ data ['latitude '] <=41.058964 ,:]
# 画 经 纬 度 分 布 图
sns . set ( style ='darkgrid ')
sns . relplot ( x ='longitude ', y ='latitude ', data = data )
plt . show ()
# 字 符 串 转 时 间
data ['date time '] = data ['date time ']. apply ( lambda x : datetime . strptime (x ,'%Y -%m -%d %H:%M:%S'))
# 重置索引
data = data . reset_index ( drop = True )
# 经 纬 度 计 算 函 数
def haversine ( lon1 , lat1 , lon2 , lat2 ): # 经度 1， 纬度 1， 经度 2， 纬度 2 （ 十进 制 度数 ）
"""
Calculate the great circle distance between two points
on the earth ( specified in decimal degrees )
"""
# 将 十 进 制 度 数 转 化 为 弧 度
lon1 , lat1 , lon2 , lat2 = map ( radians , [ lon1 , lat1 , lon2 , lat2 ])
# haversine 公式
dlon = lon2 - lon1
dlat = lat2 - lat1
a = sin ( dlat /2)**2 + cos ( lat1 ) * cos ( lat2 ) * sin ( dlon /2)**2
c = 2 * asin ( sqrt ( a ))
r = 6371 # 地 球 平 均 半 径 ， 单位 为公 里
return c * r * 1000
# 选 出 间 隔 时 间 大 于 等 于 30 的数据
time = pd . DataFrame ( columns =[ 'taxi id ','date time ','longitude ','latitude '])
for i in range (1 , len ( data )):
if( data ['taxi id '][ i ]== data ['taxi id '][ i -1]):
# dis = haversine ( data [ ' longitude '][i], data [ ' latitude '][i], data [ ' longitude '][i -1] , data [ ' latitude '][i -1])
tim =( data ['date time '][ i ] - data ['date time '][ i -1]). total_seconds ()/60
if( tim >=30):
time = time . append ( pd . DataFrame ([ data . loc [i -1 ,:]. values ] , columns =[ 'taxi id ','date time ','longitude ','latitude ']))
# 计 算 汽 车 不 同 点 坐 标 速 度
time = time . reset_index ( drop = True )
sudu =[]
for i in range (1 , len ( time )):
if( time ['taxi id '][ i ]== time ['taxi id '][ i -1]):
dis = haversine ( time ['longitude '][ i ] , time ['latitude '][ i ] , time ['longitude '][ i -1] , time ['latitude '][ i -1])
tim =( time ['date time '][ i ] - time ['date time '][ i -1]). total_seconds ()/60
if( tim !=0):
su =( dis /( tim *60))
sudu . append ( su )
# 筛 选 出 符 合 条 件 的 需 求 点
sudu = pd . DataFrame ()
for i in range (1 , len ( time )):
if( time ['taxi id '][ i ]== time ['taxi id '][ i -1]):
dis = haversine ( time ['longitude '][ i ] , time ['latitude '][ i ] , time ['longitude '][ i -1] , time ['latitude '][ i -1])
tim =( time ['date time '][ i ] - time ['date time '][ i -1]). total_seconds ()/60
if( tim !=0):
su =( dis /( tim *60))
# tim =( data [ ' date time '][i] - data [' date time '][i -1]). total_seconds ()/60
if( su >=0 and su <=1):
sudu = sudu . append ( pd . DataFrame ([ time . loc [i -1 ,:]. values ] , columns =[ 'taxi id ','date time ','longitude ','latitude ']))