联邦学习开山之作:Communication-Efficient Learning of Deep Networks from Decentralized Data 带你走进最初的联邦学习 论文精读
原文链接:Communication-Efficient Learning of Deep Networks from Decentralized Data (mlr.press)
该论文是最早提出联邦学习的论文,作者结合背景提出了联邦平均的算法,并作了相应验证实验。
ABS
随着移动设备的用户增加,产生了大量的分散数据。这些分散数据通常是涉及用户隐私的,所以想要将数据集中起来进行训练是不现实的,作者提出一种能够在各移动设备上训练一个联合模型的方法——Federated Learning。该方法同时能够提高通信效率,相比于同步的随机梯度下降(synchronized stochastic gradient descent),通信耗时下降到原来的 1 10 \frac 1 {10} 101至 1 100 \frac 1 {100} 1001。
1 INTRO
手机和平板用户的增多以及用户随身携带意味着会产生大量的数据,这些数据有着巨大的价值,可以通过对这些数据进行训练来提升用户的体验,但是这些数据是设计用户隐私的,将数据直接收集起来是不合法的。
联邦学习对模型训练与整体数据的需求进行解耦(各方独自训练),这样做一方面能够保护用户隐私,另一方面攻击方想要获得数据只能攻击各个用户,而不能直接攻击中心服务器(中心服务器没有用户的数据)。
本文的贡献:
- 指明了对于分散数据进行机器学习的方向(即提出了联邦学习);
- 一种联邦学习的方法(该方法是各个客户端进行SGD和服务器进行模型平均的有机组合);
- 对提出的方法进行广泛的具有实践意义的评价。
联邦学习的特点:
- 数据大都来自于真实数据训练效果更加贴合实际;
- 数据高度敏感且相对于单个用户来说,数据量非常大;
- 对于有监督学习,可以通过与用户的互动轻松对数据进行标号。
联邦学习对于隐私性的保护:
- 会进行通信的数据只有需要的更新,这保证了用户数据的安全;
- 更新数据不需要保存,一旦更新成功,更新数据将被丢失;
- 通过更新数据对原始数据的破解几乎不可能。
联邦学习与分布式学习有着几个显著的不同:
- 数据分布非独立同分布:不同的用户有着不同的行为;
- 数据分布不平衡:指某些参与者的数据可能很多,而某些参与者数据可能很少;
- 大量的参与者:一个软件的用户可能非常多(例如某款输入法);
- 受限的通信:参与者的信号可能非常差,甚至出现离线的情况;
联邦学习需要处理以下问题:
- 各个参与方的数据可能会发生改变(例如删除、添加、编辑照片);
- 参与方的数据分布非常复杂(不同的群体的手机使用情况差异可能会非常大)。
本论文的实验环境是一个可控的环境,主要用于解决非独立数据分布和不平衡数据分布的问题:
- 实验中固定有 K K K个参与者,参与者的数据集固定不发生更改;
- 每一轮开始时,选择 C ∗ K ( 0 ≤ C ≤ 1 ) C*K(0\le C\le1) C∗K(0≤C≤1)个参与者(实验发现当参与者的数量超过某个值是效果会出现下降,所以只选择部分的参与者),服务器将最新的参数下发给选中的参与者,参与者进行联邦学习(包含训练、联邦聚合等);
通常情况下(对于数据集中分布),我们需要:
m i n w ∈ R d f ( w ) = 1 n ∑ i = 1 n f i ( w ) \underset {w\in R^d}{min} f(w) = \frac 1 n\sum_{i=1}^nf_i(w) w∈Rdminf(w)=n1i=1∑nfi(w)
上式中的 f i ( w ) f_i(w) fi(w)代表样本 i i i的损失。
在联邦学习中,我们需要做出一定的变形:
f ( w ) = ∑ k = 1 K n k n F k ( w ) F k ( w ) = 1 n k ∑ i ∈ P k f i ( w ) \begin{aligned} &f(w) = \sum_{k=1}^K\frac {n_k} nF_k(w)\\ &F_k(w)=\frac 1 {n_k}\sum_{i \in P_k}f_i(w) \end{aligned} f(w)=k=1∑KnnkFk(w)Fk(w)=nk1i∈Pk∑fi(w)
上式中的 K K K代表参与更新的参与方个数, n n n代表总共数据个数, n k n_k nk代表第 k k k个参与方拥有的数据个数, F k ( w ) F_k(w) Fk(w)代表第 k k k个参与方的平均损失, f i ( w ) f_i(w) fi(w)代表样本 i i i的损失, P k P_k Pk代表第 k k k个参与方的数据索引集合。
在满足独立同分布的数据中(传统的分布式机器学习中,数据统一随机的下放至每个参与方), E [ F k ( w ) ] = f ( w ) E[F_k(w)]=f(w) E[Fk(w)]=f(w)(也就是样本平均的期望是与总体期望相同),但是在联邦学习中数据往往不是独立同分布的,这会导致, F k ( w ) F_k(w) Fk(w)并不能很好的对 f ( w ) f(w) f(w)进行近似。
联邦学习与传统数据中心计算的不同:
- 传统的数据中心计算,往往通信的消耗是相对较小的,计算的时间是相对较大的,联邦学习正好相反(用户可能只会在特定的时间才回进行上传,例如睡觉时,而由于用户的处理器往往不会太差,计算的耗费相对就会较小);
有两种方法能够缓解联邦学习中通信耗时的问题(核心都是让用户进行大量的计算,这样能减少通信时间的占比):
- 增加并行度,让更多的参与者进行计算;
- 增加计算度,让一个参与者进行更多的计算。
相关工作介绍:
- 传统的分布式学习考虑的是平衡的分布(各个参与方的计算量与各自的计算能力相匹配)和独立同分布(各方的数据是独立同分布的);
- 传统的分布式学习只会进行一次集中更新,已经被证明,这样训练出来的模型在最坏情况下可能会比在单个参与方训练的模型效果差。
2 The Federated Averaging Algorithm
Federated SGD:当选择 C = 1 C=1 C=1并且使用SGD进行联邦学习,本文将这种基准定义为Federated SGD,一种简单的实现如下:
- 选取 C = 1 C=1 C=1,即每次所有结点都参与计算;
- 对于参与方 k k k,计算 g k = ∇ F k ( w t ) g_k=\nabla F_k(w_t) gk=∇Fk(wt),并将计算结果发送至服务器;
- 服务器对各方的梯度进行聚合: w t + 1 = w t − η ∑ k = 1 K n k n g k w_{t+1}=w_t-\eta \sum_{k=1}^K \frac {n_k}n g_k wt+1=wt−η∑k=1Knnkgk;
同时为了提升各个参与方的计算量,作者提出Federated Averaging:
- 对于参与方 k k k,计算 w t + 1 k = w t k − η g k w_{t+1}^k = w^k_t-\eta g_k wt+1k=wtk−ηgk,同时将计算结果发送至服务器;
- 服务器对参数进行聚合: w t + 1 = ∑ k = 1 K n k n w t + 1 k w_{t+1}=\sum_{k=1}^K\frac {n_k} n w_{t+1}^k wt+1=∑k=1Knnkwt+1k。
这种方法的好处在于:参与方在发送参数之前可以进行多次的参数计算,这也就增加了参与方的计算量,Federated SGD是一种同步算法(需要等待所有方计算完梯度),而Federated Averaging并不算完全的同步算法(可以根据情况调整每一方进行计算的次数,但是还是会有同步操作)。
Federated Averaging的伪代码如下:

Federated Averaging中参与方 k k k的参数更新次数为: μ k = E n k B \mu_k=E\frac {n_k} B μk=EBnk。
作者对于不同的聚和权重以及参数的初始化方法进行了实验:
- 作者以两个参与方为例,分别进行了几种实验;
- 第一种实验对两个参与方采用不同的随机种子对参数初始化,第二种实验对两个参与方采用相同的随机种子对参数进行初始化;
- 聚合采用 w t + 1 = θ w t 1 + ( 1 − θ ) w t 2 , θ ∈ [ − 0.2 , 1.2 ] w_{t+1} = \theta w_t^1 + (1-\theta) w_t^2,\ \theta\in[-0.2,1.2] wt+1=θwt1+(1−θ)wt2, θ∈[−0.2,1.2];
- 在MNIST上进行训练。
实验结果如下图:
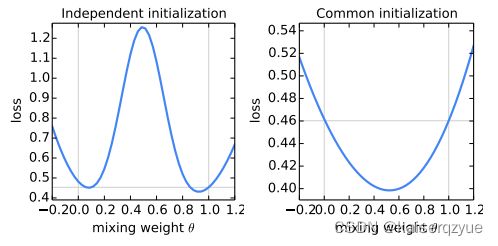
(左图为不同的随机种子进行初始化,右图为相同的随机种子进行初始化;横轴代表 θ \theta θ的取值,纵轴代表损失,注意两图纵轴的损失的刻度不同)
实验结果表明:使用相同的随机种子进行初始化,同时使用最符合常识的聚合方法( θ = 1 2 \theta=\frac 1 2 θ=21)效果是最好的。
3 Experimental Results
3.1 Datasets
实验数据集:
- MNIST:包含手写的阿拉伯数字0-9图片(每张图片只有一个数字),目标是对输入图片中的数字进行识别;
- 从The complete Works of William Shakespeare构造(输入是句子)一个数据集用于语言模型的训练记作Play&Role,目标是对输入进行下一个词语的预测。
对于上述的两组数据集会分别产生四类数据集应用于不同的实验:
- MNIST + IDD + balanced:将MNIST随机地划分成 100 100 100份(实验中有 100 100 100个参与者),每份有 600 600 600个样例;
- MNIST + Non-IDD + balanced:将MNIST的图片按照包含的数字进行排序,然后将图片等间距的分成 100 100 100份,这意味着,每个参与者的数据集最多只有两种数字;
- Play&Role + Non-IDD + unbalanced:记录每一场台词超过两句的人物数量(一共有 1146 1146 1146个),人物数量即参与方的个数,每个参与方拥有的数据即某个人物的在某一场的台词(这意味着有的参与者的数据量非常大,有的非常小,这显然是unbalanced,而数据同样显然是Non-IDD);
- Play&Role + IDD + balanced:将上述所有的台词组合起来,随机的下发给 1146 1146 1146个参与者。
3.2 Models
实验用到的模型:
- MNIST 2NN:一个有着两个隐藏层的多层感知机,用于MNIST数据集的训练;
- CNN:一个使用卷积窗口大小为 5 5 5的卷积神经网络,用于MNIST数据集的训练;
- LSTM:长短期记忆,用于Play&Role模型的训练
3.3 Experiment 1
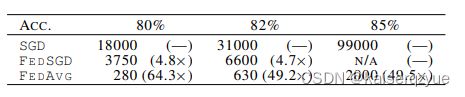
实验一:增加并行度实验,所谓增加并行度就是增加参与计算的结点数量,通过增加 C C C实现,下表展示了在MNIST上不同的 C C C对于收敛速度的影响:
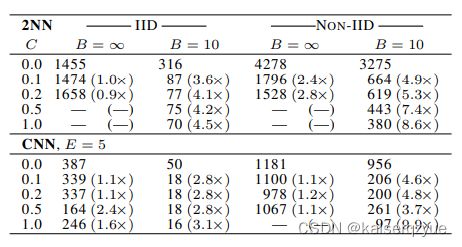
(表数字代表到达测试精度 99 % 99\% 99%(CNN)或者 97 % 97\% 97%(2NN)所需要的轮数(轮数是通过线性插值的方法计算出来),每个表的第一行代表基准, C = 0 C=0 C=0代表每轮只选择一个结点进行计算, B B B代表每个结点的批量大小(如Algorithm 1描述), B = ∞ B=\infty B=∞代表每个节点迭代时选取自己拥有的所有数据, E E E代表结点的Epoch,图中的“—”代表在规定时间内没有达到指定精度)
当参与计算的结点增大到一定值时,收敛速度有可能会有所下降,所以一般不会让所有的结点都参与计算。
3.4 Experiment 2
实验二:增加每个节点的计算量,通过改变 μ \mu μ(结点参数更新次数)来改变节点的计算量,而 μ = E n k B \mu = E \frac {n_k} B μ=EBnk(见Algorithm 1)所以通过减少 B B B或者增加 E E E可以增加结点的计算量。实验的结果如下图所示(本次试验中固定 C = 0.1 C=0.1 C=0.1):
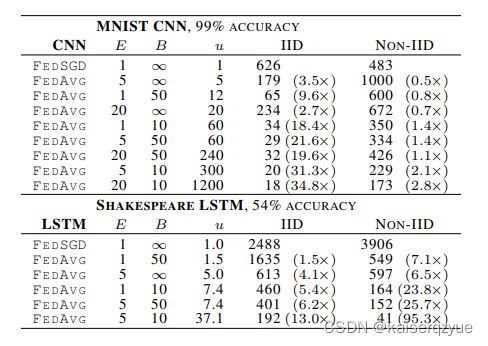
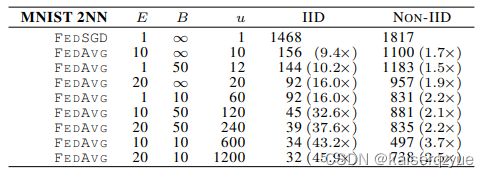
可以看到当单个节点的计算量增加时,整体收敛所需要的轮数也减少了。
实验二中出现了一个有趣的现象:在CNN中,当 E = 1 , B = ∞ E=1,B=\infty E=1,B=∞时,FedSGD算法在 1200 1200 1200轮之后达到了 99.22 % 99.22\% 99.22%准确率,而FedAVG在 B = 10 , E = 20 B=10,E=20 B=10,E=20时,300轮就达到了 99.44 % 99.44\% 99.44%的准确度。这一点是不符合常识的,因为FedSGD效果应该等价于将数据全部汇总进行训练,而作者给出了这种现象的解释:FedAVG丢失整体性类似发挥了dropout的效果。
3.5 Experiment 3
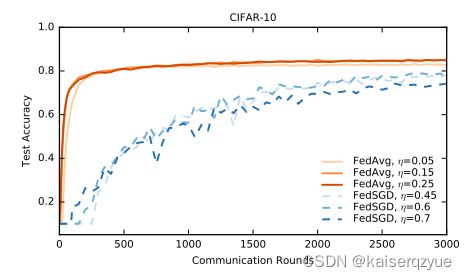
实验三:参与方极致利用自己数据,在该实验中,参与方会尽可能进行计算( E E E增大),理论上如果 E E E趋向于无穷大,那么初始化参数的影响就会被忽略(只要他们能够到达同一个局部最优解),实验结果如下图所示:
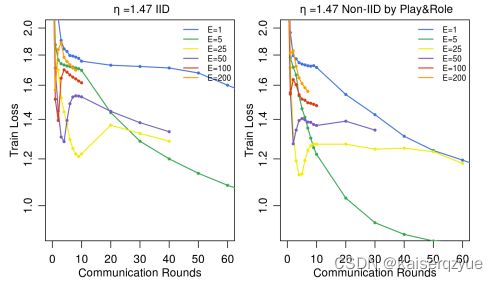
从上图中可以看到当 E E E增大时,损失反而上升了,同时出现了巨大的抖动,作者给出的原因是:实验中学习率是固定的,当 E E E增大时,在后续进行训练时,学习率会变得相对较大,所以出现了抖动。
3.6 Experiment 4
3.7 Experiment 5
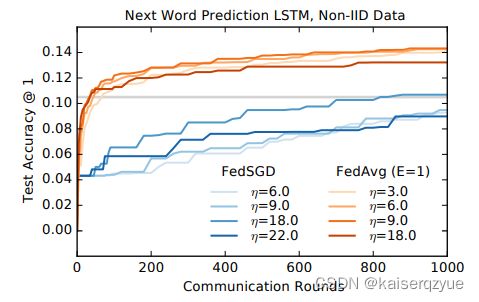
实验五:大规模的长短期记忆实验,即对Play&Role数据集进行训练,训练结果如下图:
4 Conclusions and Future Work
结论:实验结果表名联邦学习可以应用到实际工程中。
未来工作:未来工作的方向将会包括安全多方计算,对隐私保护的更强的保证。