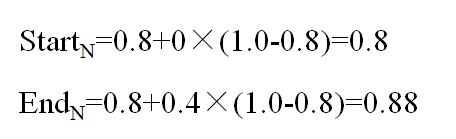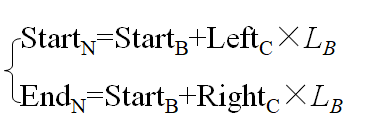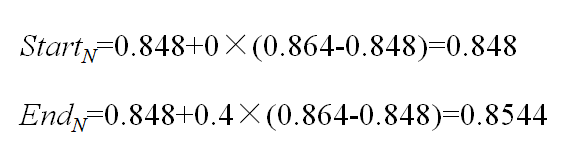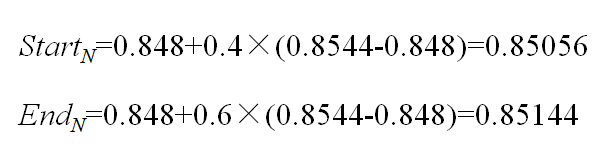【数字图像处理与应用】Lecture 16 图像压缩(2)

数字图像处理与应用 Class 16. 20200622

Lecture 16 Compression

--Lossless Image Compression

  #Variable length coding(Eliminate coding redundancies)

         Huffman coding

         Arithmetic coding

  #LZW coding (Reduce interpixel redundancies)

  #Hybrid Coding

--Lossy Image Compression

---

Arithmetic coding

源符号和码字之间不存在一一对应关系。

一个完整的源符号序列被分配一个算术码字。

码字定义了0到1之间的实数区间。

随着消息中符号数量的增加，用于表示它的间隔会变小。

而表示间隔所需的信息单位(比特)的数量也会变大。

栗子：

对于编码的信息源为“dacab”，每个源符号的概率为:P(a)=0.4,P(b)=0.2,P(c)=0.2, P(d)=0.2

在编码过程开始时，假设信息源占据整个半开区间[0,1)，根据概率将每个符号的初始区间初步细分为四个区域:a=[0,0.4)， b=[0.4, 0.6)， c=[0.6, 0.8)， d=[0.8, 1.0)

对于“d”的第一个编码符号，其初始间隔为[0.8,1.0);

对于第二个符号“a”，因为前一个符号“d”被限制在[0.8,1.0)中，所以“a”的值应该在[0,0.4)子区间[0.8,1.0)中，那么

  即符号“da”的编码间隔在[0.8,0.88)。

其中StartN、EndN为新间隔的开始和结束位置，StartB为前间隔的开始位置，LB为前间隔的长度。LeftC和RightC是当前代码间隔的左右边界。

对于第三个符号“c”，它应该在[0.8,0.88)的子区间[0.6,0.8)内，则: 

对于第四个符号“a”:

对于第五个符号“b”:

现在，源信息“dacab”已经被描述为一个实数区间[0.85056,0.85144]，或者说在这个区间内的任意实数都可以用来表示源信息。

我们可以将区间[0.85056,0.85144)表示为二进制形式[0.110110011011,0.110110011110]。

我们发现0.1101100111在这个区间内，且长度最短。然后将其作为输入序列符号“dacab”的输出。

因为所有编码的结果都包括“0”。，则可以删除它，并以1101100111作为本例的算术编码结果。

每个字符用8bit，5个字符共40bit，现在只需用10bit。

十进制小数---->二进制小数 的计算方式

二进制小数---->十进制小数 的计算方式

1977年由兰佩尔和齐夫发明，1984年由韦尔奇改进(像素间冗余)。

从那时起，出现了许多变化和改进。

美国专利号4,558,302,LZW压缩已经集成到多种主流成像文件格式中:

包括图形交换格式(GIF)。

标记图像文件格式(TIFF)。

和可携式文件格式(PDF)。

 

LZW(Lempel-Ziv-Welch) Coding

Assigns fixed-length code words to variable length sequences of source symbols.

Requires no priori knowledge of the probability of occurrence of the symbols to be encoded. 不需要先验知识

LZW编码在概念上非常简单。

在编码过程的开始，构造一个包含要编码的源符号的码本或“字典”。

举个栗子：8位单色图像

字典的前256个单词的灰度值为0,1,2，···255。

当编码器按顺序检查图像的像素时，不在字典中的灰度级序列被放置在算法确定的位置。

例如，如果图像的前两个像素是白色的，序列255-255可能被分配到位置256，该地址位于为灰度0~255保留的位置之后。

下一次，当遇到255-255时，代码字256，即包含该序列的位置的地址，用来表示它们。

如果在编码过程中使用了一个9位的512字字典，那么用于表示两个像素的原始(8+8)位将被替换为一个9位码字。

字典的大小是一个重要的系统参数。

如果它太小，匹配的灰度序列检测的可能性就小。

如果太大，码字的大小将对压缩性能产生不利影响。

 

编码

定义两个变量:

    S1: S1是一个临时变量

    S2: S2按像素存储输入数据

它们在开始时被初始化为空。

图像通过以从左到右、从上到下的方式处理像素进行编码。

将每个像素逐个读入S2:

     如果流S1+S2位于条目中，则不输出任何内容，且S1=S1+S2。

     否则，输出S1的条目索引，并将新的序列S1+S2添加到字典条目，S1=S2。

     读取所有像素后，输出S1的条目索引。

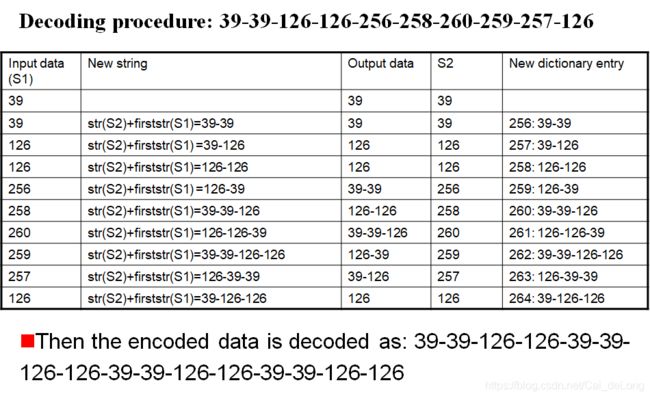
将图像编码为:39-39-126-126-256-258-260-259-257-126

LZW算法将原来的168=128位图像压缩为910=90位(10个9位代码)。

得到的压缩比是128/90=1.42

解码

定义两个变量:

    ---S1:逐一存储输入数据(编码数据)。

    ---S2:一个临时变量。

    ---它们被初始化为空。

将每个像素逐个读入S1:

如果S1位于索引中，则输出相应的值，否则输出str(S2)+firststr(S1)。

将str(S2)+firststr(S1)添加到字典条目S2=S1。

Dictionary	Entry
0	0
1	1
…	…
255	255
256	-
…	…

LZW编码的一个独特特性是在对数据进行编码时创建编码字典或代码本。

值得注意的是，LZW解码器构建的解压字典与编码器中的完全相同。

字典没有保存在压缩文件中。

大多数实际应用程序都需要一种策略来处理字典溢出。

    是在字典满时刷新或重新初始化，并使用一个新的初始化的字典继续编码。

    监控压缩性能和冲洗字典。

开始用比如9位的字典存储，之后如果空间不够，则使用10位字典代替原来的进行初始化

Hybrid Coding

混合编码的一个例子:

信息源“aaaabbbccdeeeeefffffff”，数据大小22*8=176(位)

如果用跑长法编码:a4b3c2d1e5f7，数据大小为6*(8+3)=66(位)

压缩比为:176:66=2.67

如果用霍夫曼法编码:

得到:f=01, e=11, a=10, b=001, c=0001, d=0000

压缩比为:8:2.4=3.33

结合run-length和Huffman:

可编码为“10400130001200001115017”，数据大小为(2+3)+(3+3)+(4+3)+(4+3)+(2+3)+(2+3)+(2+3)=35(位)

压缩比为:176:35=5.03

Lossy Image Compression

有损图像压缩

--为什么有损?

--一个简单的例子

有损变换编码

--图像变换选择

--小波编码

--联合摄影专家组(JPEG)

在大多数与消费电子相关的应用中，无损压缩是不必要的。我们关心的是解码图像的主观质量，而不是强度值。降低重建图像的精度，以换取增加的压缩。如果产生的失真是可以容忍的，那么压缩的增加是有效的。

通过松弛，可以实现更高的压缩比(CR)。

许多有损编码技术能够再现:

可识别的单色图像的数据已被压缩超过100:1。

在10:1到50:1之间的图像和原始图像几乎没有区别。

然而，单色图像的无损编码很少导致3:1以上的数据减少。

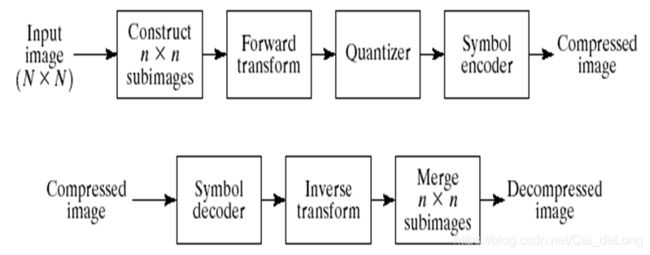
Transform Coding

前面讨论的编码技术直接对图像的像素进行操作，因此是空间域方法。

现在我们来看看基于修改图像变换(变换编码)的压缩技术。

一个线性的，可逆的变换(如傅里叶变换)被用来映射图像到一组变换系数，然后量化和编码。

对于大多数自然图像，大量的(高频)系数具有较小的量级，可以粗量化，图像失真很小。

除了DFT，我们还有圆盘

为了进行图像压缩，变换操作应为:

  ---去关联(“打破”)相关性或者把尽可能多的信息压缩到最小的变换系数中。

  ---基变换函数独立于输入图像。

  ---快速计算。

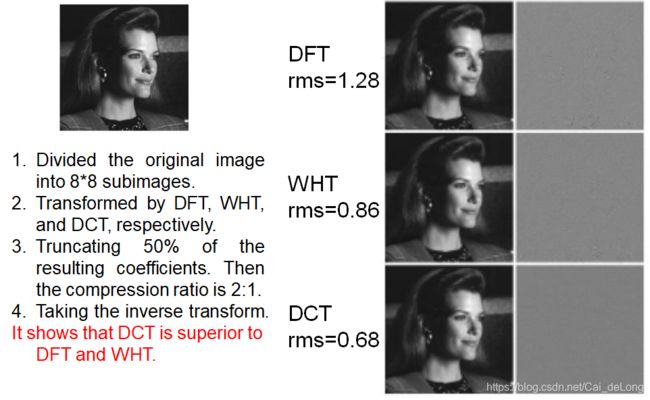
  ---典型的转换:

• DFT变换

• DCT变换

• 沃尔什阿达玛变换

• KL变换

DFT

DCT

2D DCT

WHT

  

Transform Selection

KL Transform

Karhunen-Loeve变换(KLT)

最优变换，比之前的变换更好。

基函数是与图像相关的。

不存在快速算法。

在图像压缩中不是很有用。

通常用于比较。

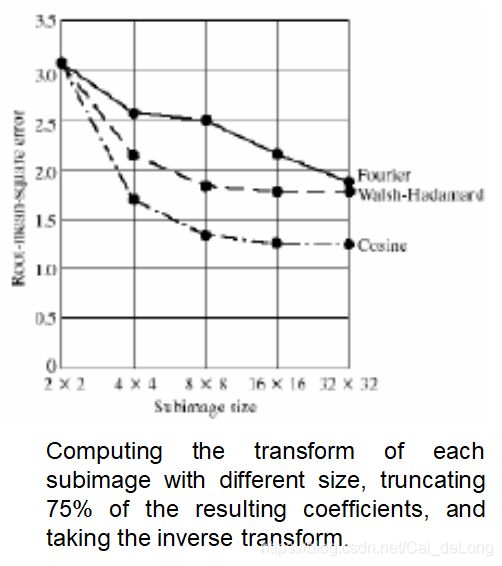
子图象尺寸选择:

子图像的大小对变换编码误差和计算复杂度有很大影响。

在大多数应用中，图像被细分，使相邻子图像之间的相关冗余降低到可以接受的程度。

通常，压缩级别和计算复杂度都会随着子图像大小的增加而增加。

最流行的尺寸是8*8或16*16。

Wavelet Transform