麻雀优化算法 优化XGBoost的参数 python代码
文章目录
- 麻雀优化算法
- 麻雀优化算法的改进
-
- 加入Ten混沌序列
- XGBoost原理
- 麻雀优化算法优化XGBoost
-
- 参数范围
- 部分代码
- 画图
- 优化结果
-
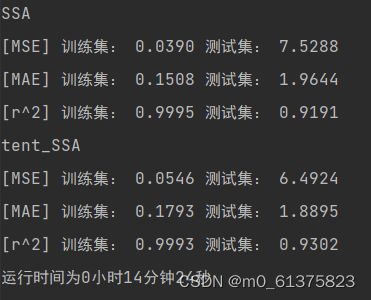
- 评价结果和运行时间
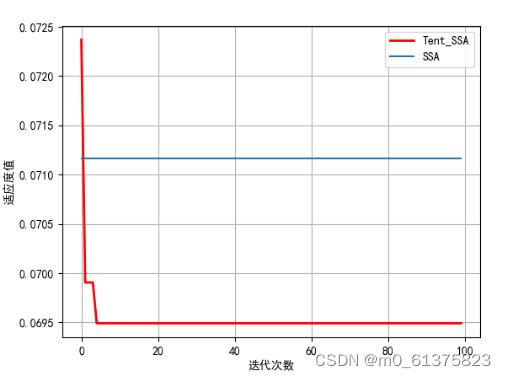
- 适应度曲线
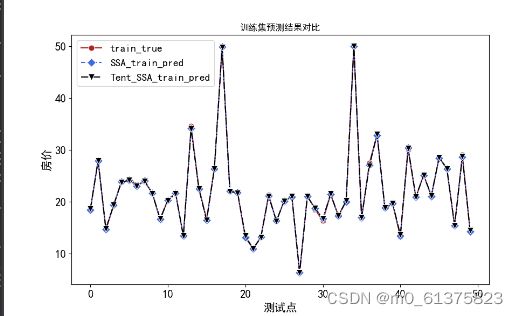
- 训练集结果
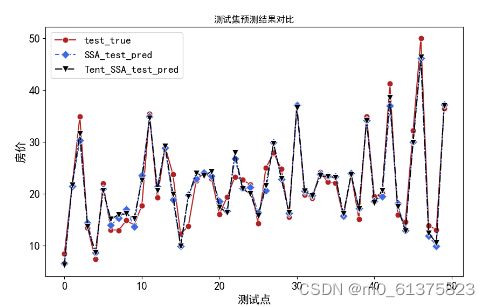
- 测试集结果
麻雀优化算法
麻雀优化算法是2020年提出来的,该算法利用麻雀的角色分工和协作机制高效搜索,具有全局优化性能好、寻优性能强的特点,适合与其他技术相融合以改进算法性能。具体的代码可以看我写的这一篇。麻雀优化算法的python实现
麻雀优化算法的改进
加入Ten混沌序列
Tent混沌序列,用此混沌序列对部分陷入局部最优的个体进行混沌扰动,促使算法跳出限制继续搜索。Tent混沌序列产生初始种群Tent映射表达式为,
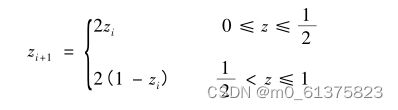
详细的算法过程见论文
吕鑫,慕晓冬,张钧,王震.混沌麻雀搜索优化算法[J].北京航空航天大学学报,2021,47(08):1712-1720.
XGBoost原理
这几年来各种机器学习比赛中什么算法风头最盛,XGBoost可谓是独孤求败了。从2016年开始,各大竞赛平台排名前列的解决方案逐渐由XGBoost算法统治,业界甚至将其称之为“机器学习竞赛的胜利女神”。Github上甚至列举了在近年来的多项比赛中XGBoost斩获的冠军列表,其影响力可见一斑。
它由陈天奇所设计,致力于让提升树突破
自身的计算极限,以实现运算快速,性能优秀的工程目标。和传统的梯度提升算法相比,XGBoost进行了许多改进,它能够比其他使用梯度提升的集成算法更加快速,并且已经被认为是在分类和回归上都拥有超高性能的先进评估器。
该算法在梯度提升决策树(GBDT)算法的基础上对损失函数进行二阶泰勒展开并且添加了正则项,有效地避免了过拟合同时加快了收敛的速度。XGBoost算法可以表示成一种加法的形式,如式所示, 代表第 个子模型,
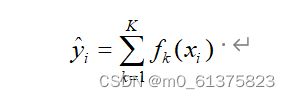
XGBoost的目标函数由损失函数和正则项两个部分组成,表示前 次迭代的预测值并且.他们防止决策树过拟合或过于复杂。
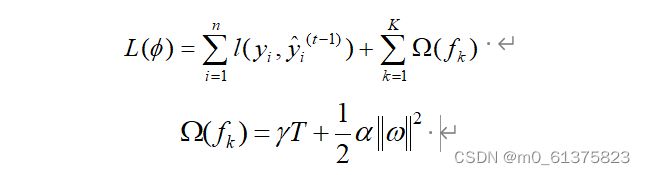
对式所示的目标函数使用泰勒公式展开可得:
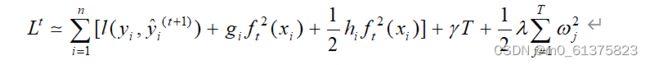
主要原理可以参考其他博客。
麻雀优化算法优化XGBoost
主要对XGBoost中的n_estimator,learning_rate,max_depth,gamma这四个参数进行优化。以R2为目标函数,进行寻优。使用的是python自带的数据集——波士顿房价数据集。
| 参数 | 说明 |
|---|---|
| n_estimator | 也作num_boosting_rounds这是生成的最大树的数目,也是最大的迭代次数。 |
| learning_rate | 每一步迭代的步长,很重要。太大了运行准确率不高,太小了运行速度慢。我们一般使用比默认值小一点,0.1左右就很好。 |
| max_depth | 我们常用3-10之间的数字。这个值为树的最大深度。这个值是用来控制过拟合的。max_depth越大,模型学习的更加具体。设置为0代表没有限制,范围: [0,∞] |
| gamma | 系统默认为0,我们也常用0。在节点分裂时,只有分裂后损失函数的值下降了,才会分裂这个节点。gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大,算法越保守。因为gamma值越大的时候,损失函数下降更多才可以分裂节点。所以树生成的时候更不容易分裂节点。范围: [0,∞] |
参数范围
'''分别为n_estimator,learning_rate,max_depth,gamma四个参数的范围'''
UP = [1500, 1, 500, 1]
DOWN = [0.1, 0.1, 1, 0.1]
部分代码
def training(X):
temp1 = model.score(X_test, y_test)
r2 = 1 - temp1
print(r2)
return r2
UP = [1500, 1, 500, 1]
DOWN = [0.1, 0.1, 1, 0.1]
# 开始优化
#SSA
ssa = SSA(training, n_dim=4, pop_size=30, max_iter=100, lb=DOWN, ub=UP,verbose=True)
ssa.run()
print('best_params is ', ssa.gbest_x)
print('best_precision is', ssa.gbest_y)
# ten-SSA优化
pop = 30 #种群数量
MaxIter = 100
dim =4
fobj = training
lb = [ 0.1, 0.1, 1, 0.1]
ub =[1500, 1, 500, 1]
GbestScore,GbestPositon,Curve = Tent_SSA.Tent_SSA(pop,dim,lb,ub,MaxIter,fobj)
画图
plt.plot(Curve,'r-',linewidth=2,label='Tent_SSA')
plt.plot(ssa.gbest_y_hist, label='SSA')
plt.xlabel('迭代次数')
plt.ylabel('适应度值')
a = ssa.gbest_y_hist
plt.legend()
plt.grid()
#plt.savefig('SSA与Ten_SSA.png', dpi=500, bbox_inches='tight')
plt.show()