小样本学习(Few-Shot Learning)（二）

1. 前言

本文讲解小样本学习问题的Pretraining+Fine Tuning解法。
小样本学习(Few-Shot Learning)（一）讲解了小样本学习问题的基本概念及基本思路，并介绍了使用孪生网络解决小样本学习问题的方法。
小样本学习(Few-Shot Learning)（三）使用飞桨（PaddlePaddle）基于paddle.vision.datasets.Flowers数据集实践小样本学习问题的Pretraining+Fine Tuning解法。
本人全部文章请参见：博客文章导航目录
本文归属于：元学习系列

2. 预训练（Pretraining）

在小样本学习问题中，测试样本及其类别均不在训练集中，但是Support Set包含的类别是固定不变的。使用孪生网络解决小样本学习问题，会训练一个可以用来衡量图片之间相似度的神经网络，逐一比较Query图片和Support Set中各图片的相似度，并返回相似度最高的图片类别作为预测结果。这种小样本学习问题的解法显然没有利用Support Set中包含的类别固定不变的性质，因此并不是小样本学习问题最好的解决方法。
小样本学习问题的Pretraining+Fine Tuning解法的基本想法是在大规模数据集上预训练模型，然后在小规模的Support Set上做Fine Tuning。这种解决方法非常简单，但是准确率基本与小样本学习领域最好的方法相当。相较之下，许多非常复杂的方法的准确率没有显著高于这种非常简单的Pretraining+Fine Tuning方法。

由于小样本学习问题中Support Set包含的样本数量非常少，因此小样本学习问题的Pretraining+Fine Tuning解法与传统迁移学习中的Pretraining+Fine Tuning方法有所不同。
Pretraining阶段，搭建一个卷积神经网络用于从图片中提取特征，在大规模数据集上通过以下两个步骤训练该卷积神经网络：

1. 基于$Softmax+CrossEntropy$损失，使用标准的分类监督学习方法训练卷积神经网络；
2. 使用孪生网络中提到的方法，继续训练第1步中训练好的卷积神经网络。

深度学习实践证明，先使用交叉熵损失，基于传统的分类监督学习方法训练模型，而不是直接使用孪生网络相关方法训练模型，可以使得模型更快收敛；
使用孪生网络相关方法继续训练模型，可以使用余弦相似度（Cosine Similarity）作为损失函数，本文后续Fine Tuning阶段及预测时候会基于余弦相似度来进行小样本分类；
不同网络结构和训练方法会对最终结果产生影响。

2.1 使用预训练模型进行小样本分类

模型预训练完成后，已经可用来解决小样本分类问题了。如图一所示，给定一个3-Way 2-Shot Support Set，解决该小样本学习问题首先要用预训练好的神经网络提取特征，将所有图片全部变成特征向量。对每个类别所有图片的特征向量做平均，得到可以表征该类别的特征向量。进一步对得到的三个特征向量做归一化，形成${\mu }_1,{\mu }_2,{\mu }_3$。

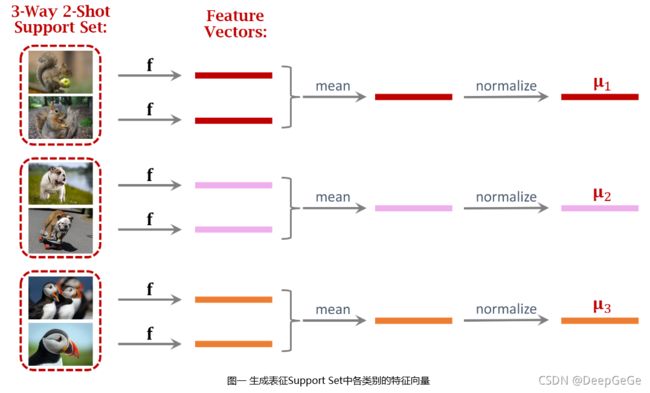
${\mu }_1,{\mu }_2,{\mu }_3$可以看做对给定Support Set各类别的表征，其 二范数 均等于一。在分类的时候，需要拿Query图片的特征向量与Support Set中各类别的特征向量进行对比。
给定Query图片$x$，按照上述提取Support Set中图片特征向量的步骤，提取Query图片特征并归一化，得到向量$q$。将从Support Set中提取的三个向量${\mu }_1,{\mu }_2,{\mu }_3$堆叠起来，形成矩阵$M$，$M=\left[\begin{array}{c}{\mu }_1^T\\ {\mu }_2^T\\ {\mu }_3^T\end{array}\right]$。将矩阵$M$与$q$相乘，并将结果输入$Softmax$函数，得到向量$p$，$p=Softmax(Mq)=Softmax\left(\left[\begin{array}{c}{\mu }_1^{T}q\\ {\mu }_2^{T}q\\ {\mu }_3^{T}q\end{array}\right]\right)$。$p$是$Softmax$函数的输出，是一个概率分布，其每个元素分别表示Query图片属于每个类别的置信度。
在Support Set的各类特征向量${\mu }_1,{\mu }_2,{\mu }_3$中，若${\mu }_1$与$q$的余弦相似度最大，则${\mu }_1^{T}q$的值比${\mu }_2^{T}q$和${\mu }_3^{T}q$大，因此向量$p$的第一个元素值最大，输出分类结果会是第一类。

3. 微调模型参数（Fine Tuning）

在大规模数据集上预训练好神经网络之后，可以在Support Set上进行Fine Tuning来进一步提高预测准确率。很多论文的实验结果表明，Fine Tuning可以大幅提高预测准确率。一篇ICLR 2020的论文实验表明，在5-way 1-shot Support Set上做Fine Tuning可以提升$2\%\sim 7\%$的准确率，在5-way 5-shot Support Set上做Fine Tuning可以提升$1.5\%\sim 4\%$的准确率。小样本学习领域很多论文中的实验都证明了，尽管Support Set非常小，但是用Support Set来训练分类器有助于提升准确率，使用Pretraining+Fine Tuning比只使用Pretraining要好很多。

假设$(x_j,y_j)$为Support Set中一个样本，其中$x_j$为图片，$y_j$为标签。使用预训练好的神经网络可以将图片$x_j$转换成特征向量$f(x_j)$。将特征向量$f(x_j)$输入$Softmax$分类器，分类器会输出概率分布$p_j=Softmax(Wf(x_j)+b)$，$p_j$的各个元素分别表示图片$x_j$属于各类别的概率。
不进行Fine Tuning，直接使用预训练模型进行小样本分类，相当于不学习$Softmax$分类器中的参数矩阵$W$和$b$，而是直接使$W=M,b$等于全0向量。$M$矩阵的每一行是Support Set中一个类别的均值向量，将$Softmax$分类器中的参数矩阵$W$设置为$M$矩阵，则分类器输出向量$p_j$的每个元素可以反映出Query图片$x_j$的特征与Support Set中各类别特征之间的相似度。

比上述直接使用预训练模型进行小样本分类更好的方法是进行Fine Tuning，在Support Set上学习$Softmax$分类器中的参数矩阵$W$和$b$。在Support Set中有几个或者几十个样本，对于每个样本$(x_j,y_j)$，计算$Softmax$分类器的输出向量$p_j$和图片$x_j$的标签$y_j$的$CrossEntropy$，将Support Set中所有样本的$CrossEntropy$相加作为目标函数，即使用Support Set中所有图片及其标签来训练$Softmax$分类器。
最小化目标函数，$min{\sum }_{j}CrossEntropy(y_j,p_j)$，使得$Softmax$分类器的输出$p_j$尽量接近图片的真实标签$y_j$。计算目标函数关于$Softmax$分类器的参数$W$和$b$的梯度，使用梯度下降法更新分类器参数。

除了学习$Softmax$分类器参数，也可以让梯度传播至卷积神经网络，更新卷积神经网络参数，使其提取的特征更有效。

3.1 Fine Tuning技巧

由于Support Set中样本数量非常少，使用上述传统迁移学习中的Fine Tuning方法训练$Softmax$分类器效果一般不好，在小样本学习领域，在Support Set上进行Fine Tuning必须使用一定技巧。

3.1.1 A Good Initialization

FineTuning阶段的目标是在Support Set中学习一个$Softmax$分类器，分类器的参数是$W$和$b$。由于Support Set中样本数量非常少，一般会把$Softmax$分类器的参数$W$初始化为$M$，$b$初始化为全0向量。
根据2.1所述使用预训练模型进行小样本分类方法，如果只使用Pretraining而不使用Fine Tuning，相当于将$Softmax$分类器的参数$W$初始化为$M$，$b$初始化为全0向量。这样设置，哪怕不进行Fine Tuning，也能够有不错的效果。因此相比较于传统迁移学习中的随机初始化，这种将将$Softmax$分类器的参数$W$初始化为$M$，$b$初始化为全0向量的方法是一种非常合理的初始化。

3.1.2 Entropy Regularization

由于Support Set非常小，因此需要在目标函数上添加正则项（Regularization）防止过拟合。在小样本学习领域，一种非常合适的Regularization方法是Entropy Regularization。
神经网络提取图片$x$中的特征，得到特征向量$f(x)$，将$f(x)$输入$Softmax$分类器，得到一个表示概率分布的向量$p$。计算Support Set中所有样本图片对应的$p$向量的Entropy，所有$p$向量的Entropy的均值即为Entropy Regularization。

Entropy Regularization是小样本学习领域一个非常合理的Regularization，其原因如下：
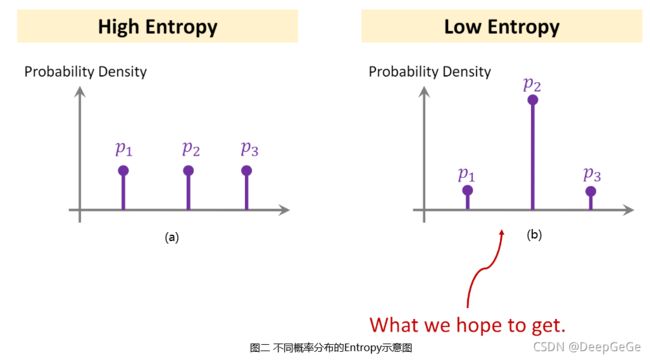
向量$p$的Entropy计算公式为：$H(p)=-{\sum }_i{p}_i\log p_i$，其可以用来衡量概率分布$p$的信息量。假设小样本分类问题中Support Set共三个类别，$Softmax$分类器输出概率分布p，分别表示每个类别的概率值。
在图二中，左侧图(a)对应的$p_a$表明输入图片属于三个类别概率几乎相同，这种情况说明分类器无法判别输入图片属于哪一类。右侧图(b)对应的$p_b$表明输入图片属于第二个类别概率非常大，属于其余类别概率很小，即分类器有较大把握认为输入图片属于第二类。
由于左侧图(a)对应的$p_a$各个概率值几乎相同，因此$p_a$对应的Entropy非常大，右侧图(b)对应的$p_b$某个概率值非常大，其余概率值很小，因此$p_b$对应的Entropy非常小。左侧图(a)表明分类器无法区分输入图片的类别，右侧图(b)表明分类器有相当大的把握将图片分到某一个类别。
右侧图(b)所示情况即我们期望的概率分布形式，Entropy越小则分类器输出概率分布$p$越接近于右侧图(b)所示形式，因此可以在小样本学习领域使用Entropy Regularization。

3.1.3 Cosine Similarity+Softmax Classifier

第三个技巧是结合Cosine Similarity和$Softmax$分类器，根据小样本学习领域的一些最新的论文，这个很小的改进技巧可以显著提高分类准确率。
假设Support Set中共三类，则$Softmax$分类器输出概率分布$p=Softmax(Wq+b)=Softmax\left(\left[\begin{array}{c}{w}_1^{T}q+b_1\\ w_2^{T}q+b_2\\ w_3^{T}q+b_3\end{array}\right]\right)$。
将Cosine Similarity和$Softmax$分类器相结合，只需将$w_{i}q$替换成$w_i$和$q$的Cosine Similarity，即$p=Softmax\left(\left[\begin{array}{c}sim(w_1,q)+b_1\\ sim(w_2,q)+b_2\\ sim(w_3,q)+b_3\end{array}\right]\right)$，其中$sim(w_i,q)=\frac{w_i^{T}q}{||w_i|{|}_2||q|{|}_2}$，即$w_i$和$q$的Cosine Similarity。

4. 后记

解决小样本分类问题最简单有效的方法是在大规模数据集上预训练一个神经网络，并在Support Set中使用上述三个技巧进行Fine Tuning。用训练好的神经网络提取特征，比较两张图片在特征空间上的相似度，从而判断Query图片的类别。
本文详细介绍了小样本分类问题的Pretraining+Fine Tuning解法。小样本学习(Few-Shot Learning)（三）使用飞桨（PaddlePaddle）基于paddle.vision.datasets.Flowers数据集实践小样本学习问题的Pretraining+Fine Tuning解法。

相关论文：

1. Feifei L , Fergus R , Perona P . One-shot learning of object categories[J]. IEEE Trans Pattern Anal Mach Intell, 2006, 28(4):594-611.
2. Bromley J , Guyon I , Lecun Y , et al. Signature Verification Using a Siamese Time Delay Neural Network[C]// Advances in Neural Information Processing Systems 6, [7th NIPS Conference, Denver, Colorado, USA, 1993]. 1993.
3. G Koch, R Zemel, R Salakhutdinov. Siamese Neural Networks for One-shot Image Recognition.
4. Schroff, Kalenichenko, & Philbin. Facenet: A unified embedding for face recognition and clustering. In CVPR, 2015.
5. Dhillon G S , Chaudhari P , Ravichandran A , et al. A Baseline for Few-Shot Image Classification[J]. arXiv, 2019.
6. Chen Y , Wang X , Liu Z , et al. A New Meta-Baseline for Few-Shot Learning[J]. 2020.
7. Authors A . A CLOSER LOOK AT FEW-SHOT CLASSIFICATION[J]. 2019.

5. 参考资料链接

1. https://www.youtube.com/watch?v=3zSYMuDm6RU&list=PLvOO0btloRnuGl5OJM37a8c6auebn-rH2&index=3
2. https://github.com/wangshusen/DeepLearning/blob/master/Slides/16_Meta_3.pdf