Few-shot Learning

Few-shot Learning

前言：CSDN就是毒瘤，已转向博客园，博客园主页https://www.cnblogs.com/ClarkGable/

一.

1.

与传统的监督学习不同，few-shot leaning的目标是让机器学会学习；使用一个大型的数据集训练模型，训练完成后，给出两张图片，让模型分辨这两张图片是否属于同一种事物。比如训练数据集中有老虎、大象、汽车、鹦鹉等图片样本，训练完毕后给模型输入两张兔子的图片让模型判断是否是同一种事物，或者给模型兔子和狗的图片去判断

2.

训练的目的是靠着Support Set提供的一点信息，让模型判断出Query中的图片是otter这个类别，尽管训练数据集中没有otter这个类别。

k-way n-shot Support Set

k-way: the support set has k classes;

n-shot: every class has n samples.

k way表示支撑集中的类别，n shot表示支撑集中每个类别包含的样本数量

3.

随着Support Set中类别增加，分类准确率会降低

因为3选1比6选1更容易，准确率更高

同样地，Support Set中shot数量增加，分类准确率会提高

4.

idea：学习一个相似度函数

sim函数来计算两张图片x和x’的相似度，

例如两张狗的图片x₁和x₂，一张猫的图片x₃，sim(x₁,x₂)=1, sim(x₁,x₃)=0，sim(x₂,x₃)=0

基本思想：

​ （1）首先，从一个大样本数据集中学习一个相似度函数

​ （2）然后，用相似度函数来做预测

​ ①用query和support set的每一个样本逐一作比较；

​ ②找出相似度得分最高的样本

5.常用的数据集

（1）Omniglot

​ https://github.com/brendenlake/omniglot or https://www.tensorflow.org/datasets/catalog/omniglot

（2）Mini-ImageNet

二.连体网络Siamese Network

两种训练Siamese Network的方法

1.每次取两个样本，比较他们的相似度

需要用到一个大的带标签的数据集来训练神经网络，利用训练集来构造正样本Positive Samples和负样本Negative Samples

Positive Samples：每次从一个类别中随机抽取两张图片，把标签设置为1，即相似度满分，用这样的方法，也从其他类别中抽取图片，标签都设置为1；

Negative Samples：随机抽取一个类中的一张图片，排除掉这个类，再从其他类中随机抽取一张图片，把标签设置为0，即相似度为0，这样构造负样本。

搭建一个卷积神经网络来提取特征，输入图片记为x，输出特征向量记作f(x)

训练神经网络，将准备好的图片输入神经网络f，提取的两个特征向量记作h₁，h₂，z = |h₁-h₂|，再通过一个全连接层输出一个标量，最后使用sigmoid函数得到一个0~1之间的输出，这个输出就可以衡量两个图片之间的相似度，sim(x₁,x₂)。两张图片属于同一个类别，那么输出应该接近1，如果两张图片属于不同类别，那么输出应该接近0。损失函数是标签Target=1与sim(x₁,x₂)之间的差别，用来更新全连接层和神经网络f的参数（注意这里的图片输入的是同一个神经网络）之所以叫做连体网络，是这个网络的结构头部连在一起，如下图所示

这样就完成了一轮训练

负样本训练过程与之类似，只是输入时两张不同类别的照片，标签Target=0

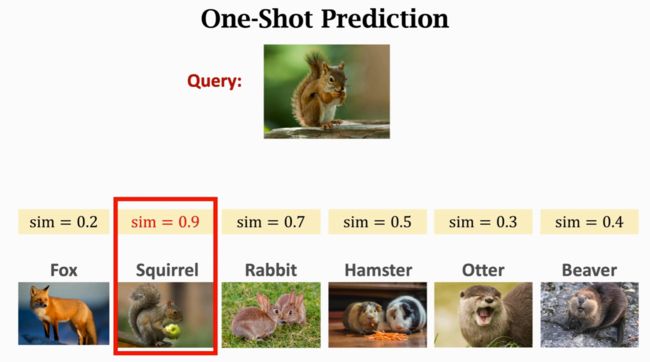
训练完成后就可以做one-shot prediction，Support Set中的六个类别都不在训练集里，将Query与Support Set逐一对比，相似度最高的就是预测结果

2.Triplet Loss

每次从训练集中选出3张图片，在这3个图片中选择一个记为x^a, anchor（锚点），选出同类别的另一张图片，记作正样本x⁺，选出其他类别中的一张图片，记作负样本x^-；

把三张图片输入卷积神经网络f提取特征向量f(x^a), f(x⁺), f(x^-)，计算f(x^a), f(x⁺)之间的二范数距离d⁺，和f(x^a)，f(x^-)之间的二范数距离d^-，d⁺应该很小，d^-应该很大；

设置超参数α为margin，如果d^-很大，d^->d⁺+α，那么损失函数为0，因为很好的区分开了两类图片，反之，损失函数为d⁺+α-d^-。

在预测时，把图片都变为特征向量，计算query与他们之间的距离，找出距离最小的

总结

三. Pretraining + Fine Tuning

大规模数据上做pretraining，小样本上fine tuning

1.Pretraining

神经网络的结构

用3-way 2-shot的SUpport Set做few-shot分类，用与训练的神经网络提取特征，将每个类别提取的两个特征向量求平均，归一化得到 μ₁，μ₂，μ₃，

提取query的特征向量，归一化得到q，将 μ₁，μ₂，μ₃堆叠起来，得到矩阵M，M与q相乘通过softmax函数得到输出p，显然μ₁与q的内积是最大的，所以会将query识别为第一类。

2.Fine Tuning

上一过程中，我们假定的W=M，b=0，其实我们可以在Support Set上学习W和b，计算Support Set所有的p_j和真实标签y_j之间的CrossEntropy，并使之最小，加上Regularization防止过拟合。

Trick1在初始化分类器时，可以把W初始化为M，b=0

Trick2 Regularization使用Entropy Regularization

因为输出的q是类别的概率值，左边这种情况说明分类器无法判别query属于哪一类，这种情况的entropy很高；我们希望的情况是右边的这种情况，分类器认为query属于第二类

Trick3 在通过softmax函数时，将W^Tq变为cos(W,q)，能够提升准确率

总结

也可以在插入中间步骤Fine Tuning