【演化计算】麻雀优化算法相关原理及代码(Matlab+Python)
目录
- 一、麻雀优化算法简要概述
- 二、算法起源
- 三、算法原理
- 四、算法流程
- 五、核心代码
- 六丶运行结果
- 七丶参考
- 八丶相关代码(Matlab+Python版本):
一、麻雀优化算法简要概述
麻雀优化算法(sparrow search algorithm,SSA)是受麻雀觅食行为和反捕食行为启发而提出的一种新型群体智能优化算法,在2020年提出,具体可抽象为发现者-追随者模型,并加入侦查预警机制。
二、算法起源
在麻雀觅食的过程中,可将其整体种群分为发现者和追随者,发现者在种群中负责寻找食物并为整个麻雀种群提供觅食区域和方向,而追随者则是依赖发现者来获取食物。为了获得食物,麻雀可采用发现者和追随者两类行为策略进行觅食。同时种群中会选取一定比例的个体进行侦查预警,若发现危险则选择放弃食物,保证安全。
三、算法原理
该算法主角即为麻雀,每只麻雀个体只有一项属性:位置,可表示其所寻觅到的食物所在方位。对于每只麻雀个体,其可能有三种状态的改变:1、充当发现者,带领种群寻觅食物。2、作为追随者,追随发现者觅食。3、具备警戒机制,发现危险则放弃觅食。
抽象在数学角度即:
对于麻雀种群:
X = [ x 1 1 x 1 2 … x 1 d x 2 1 x 2 2 … x 2 d … … … … x n 1 x n 2 … x n d ] X=\left[ \begin{matrix} x_{1}^{1} & x_{1}^{2} & \ldots & x_{1}^{d} \\ x_{2}^{1} & x_{2}^{2} & \ldots & x_{2}^{d} \\ \ldots & \ldots & \ldots & \ldots \\ x_{n}^{1} & x_{n}^{2} & \ldots & x_{n}^{d} \\ \end{matrix} \right] X=⎣ ⎡x11x21…xn1x12x22…xn2…………x1dx2d…xnd⎦ ⎤
式中,n表示麻雀种群的数量,d表示麻雀个体所附带的维度。
算法中,有较强搜索能力即具备较好适应度值的发现者在搜索过程中会优先获取食物。且优于发现者所具备的全局导向能力,为种群寻找食物且为加入者提供觅食方向。因此发现者需具备更大的觅食搜索范围。由此抽象其位置更新表述为:
X i d t + 1 = { X i d t ⋅ exp [ − i α ⋅ T ] , i f R 2 < S T X i d t + Γ ⋅ L , i f R 2 > S T X_{id}^{t+1}=\left\{ \begin{matrix} X_{id}^{t}\cdot \exp \left[ \frac{-i}{\alpha \cdot \Tau } \right]\begin{matrix} ,if & {{R}_{2}}
式中, X i d t X_{id}^{t} Xidt表示种群中第t代中第i只麻雀在第d维的位置。T为最大迭代次数。α为(0,1]之间的随机数。 Γ \Gamma Γ 是服从标准正态分布的随机数。 L L L表示大小为i×d,元素均为1的矩阵。 R 2 R_2 R2 ϵ[0,1]和 S T ST ST∈[0.5,1]分别表示预警值和安全值。
式中可以看出,当 R 2 R_2 R2大于 S T ST ST时,表明部分麻雀已发现危险,此时发现者值收敛应向安全位置移动,即发现者按正态分布随机移动到当前位置附近。而当 R 2 R_2 R2小于 S T ST ST时,表明当前环境不存在危险,发现者可以进行大范围的搜索操作,随着种群代数的增加, exp [ − i α ⋅ T ] \exp \left[ \frac{-i}{\alpha \cdot \Tau } \right] exp[α⋅T−i]项的取值范围将随之减少,取值的分布将变得较为均匀,即对应到麻雀个体的每一维上的值都将减少。
种群中除去发现者,剩余麻雀均为追随者。追随者的位置更新描述如下:
X i d t + 1 = { Γ ⋅ exp [ X w d t -X i d t i 2 ] , i f i > n 2 X p d t + 1 + ∣ X i d t − X p d t + 1 ∣ A + ⋅ L , o t h e r w i s e X_{id}^{t+1}=\left\{ \begin{matrix} \Gamma \cdot \exp \left[ \frac{Xw_{d}^{t}\text{-X}_{id}^{t}}{{{i}^{2}}} \right]\begin{matrix} ,if & i>\frac{n}{2} \\ \end{matrix} \\ Xp_{d}^{t+1}+\left| X_{id}^{t}-Xp_{d}^{t+1} \right|{{A}^{+}}\cdot L\begin{matrix} , & otherwise \\ \end{matrix} \\ \end{matrix} \right. Xidt+1={Γ⋅exp[i2Xwdt-Xidt],ifi>2nXpdt+1+∣ ∣Xidt−Xpdt+1∣ ∣A+⋅L,otherwise
式中, X w d t Xw_{d}^{t} Xwdt表示第t次迭代时麻雀在第d维的最劣位置。 X p d t + 1 Xp_{d}^{t+1} Xpdt+1表示种群第t+1次迭代时麻雀在第d维的最优位置。 A A A表示一个各元素为1或-1的一行多维矩阵,且 A + = A T ( A A T ) − 1 {A}^{+}={A}^{T}(A{A}^{T})^{-1} A+=AT(AAT)−1。当 i i i大于 n / 2 n/2 n/2时,表明该追求者处于十分饥饿的状态,利用一个标准正态分布随机数与以自然对数为底指数函数的积,控制其取值符合正态分布,即获取更多的能量。当 i i i小于等于 n / 2 n/2 n/2时,其过程可解释为在当前最优位置附近随机找到一处位置,且每一维据最优位置方差较小,值较为稳定。
在麻雀种群中,带有警戒机制的麻雀数量占总数的10%到20%,位置是随机产生的,位置更新公式如下:
X i d t + 1 = { X b d t + β ( X i d t − X b d t ) , i f f i ≠ f g X i d t + K [ X i d t − X w d t ∣ f i − f w ∣ + δ ] , i f f i = f g X_{id}^{t+1}=\left\{ \begin{matrix} Xb_{d}^{t}+\beta (X_{id}^{t}-Xb_{d}^{t})\begin{matrix} ,if & {{f}_{i}}\ne {{f}_{g}} \\ \end{matrix} \\ X_{id}^{t}+K\left[ \frac{X_{id}^{t}-Xw_{d}^{t}}{\left| {{f}_{i}}-{{f}_{w}} \right|+\delta } \right]\begin{matrix} ,if & {{f}_{i}}={{f}_{g}} \\ \end{matrix} \\ \end{matrix} \right. Xidt+1={Xbdt+β(Xidt−Xbdt),iffi=fgXidt+K[∣fi−fw∣+δXidt−Xwdt],iffi=fg
式中, X b d t Xb_{d}^{t} Xbdt是当前的全局最优位置。 β β β表示步长控制参数。 K K K是[-1,1]之间的一个随机数,代表麻雀移动方向。 是一个极小常数,以避免分母为0的情况出现; f i {f}_{i} fi表示第i只麻雀的适应度值, f g {f}_{g} fg和 f w {f}_{w} fw分别是当前麻雀种群的最优和最差适应度值。
即当预警麻雀处于当前最优位置,则会逃离至自身附近的位置。若不是最优位置,则逃离到当前最优位置附近。
四、算法流程
Step1:初始化种群数量、迭代次数、发现者与追随者比例。
Step2:计算适应度值,排序。
Step3:更新发现者位置。
Step4:更新追随者位置。
Step5:更新警戒者位置。
Step6:计算适应度值并更新个体位置。
Step7:判断是否满足停止条件,满足则退出。
五、核心代码
'''麻雀搜索算法'''
def SSA(pop,dim,lb,ub,Max_iter,fun):
ST = 0.6 #预警值
PD = 0.7 #发现者的比列,剩下的是加入者
SD = 0.2 #意识到有危险麻雀的比重
PDNumber = int(pop*PD) #发现者数量
SDNumber = int(pop*SD) #意识到有危险麻雀数量
X,lb,ub = initial(pop, dim, ub, lb) #初始化种群
fitness = CaculateFitness(X,fun) #计算适应度值
fitness,sortIndex = SortFitness(fitness) #对适应度值排序
X = SortPosition(X,sortIndex) #种群排序
GbestScore = copy.copy(fitness[0])
GbestPositon = np.zeros([1,dim])
GbestPositon[0,:] = copy.copy(X[0,:])
Curve = np.zeros([Max_iter,1])
for i in range(Max_iter):
BestF = fitness[0]
X = PDUpdate(X,PDNumber,ST,Max_iter,dim)#发现者更新
X = JDUpdate(X,PDNumber,pop,dim) #加入者更新
X = SDUpdate(X,pop,SDNumber,fitness,BestF) #危险更新
X = BorderCheck(X,ub,lb,pop,dim) #边界检测
fitness = CaculateFitness(X,fun) #计算适应度值
fitness,sortIndex = SortFitness(fitness) #对适应度值排序
X = SortPosition(X,sortIndex) #种群排序
if(fitness[0]<=GbestScore): #更新全局最优
GbestScore = copy.copy(fitness[0])
GbestPositon[0,:] = copy.copy(X[0,:])
Curve[i] = GbestScore
return GbestScore,GbestPositon,Curve
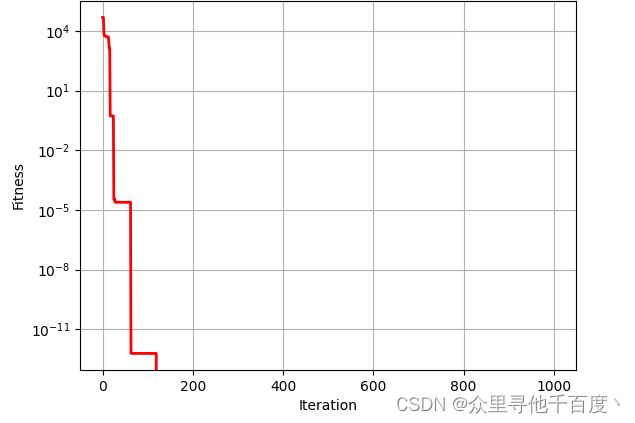
六丶运行结果
测试函数: f = ∑ i = 1 n ( ∑ j = 1 i x j ) 2 f=\sum\limits_{i=1}^{n}{{{(\sum\limits_{j=1}^{i}{{{x}_{j}}})}^{2}}} f=i=1∑n(j=1∑ixj)2
结果:
七丶参考
[1] Xue J, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems ence and Control Engineering An Open Access Journal, 2020, 8(1), 22-34.
八丶相关代码(Matlab+Python版本):
Matlab版本:https://mianbaoduo.com/o/bread/Yp2Zkpls
Python版本:https://mianbaoduo.com/o/bread/Yp2Zkplw