GNN图神经网络基础入门博客

高等数学-高等代数

欧几里得空间

一句话总结：欧几里得空间就是在对现实空间的规则抽象和推广（从n<=3推广到有限n维空间）。

欧几里得几何就是中学学的平面几何、立体几何，在欧几里得几何中，平行线任何位置的间距相等。而中学学的几何空间一般是2维，3维（所以，我们讨论余弦值、点间的距离、内积都是在低纬空间总结的），如果将这些低维空间所总结的规律推广到有限的n维空间，那这些符合定义的空间则被统称为欧几里得空间（欧式空间，Euclidean Space）。

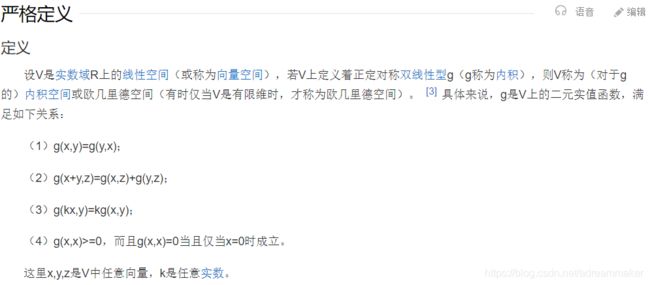
而欧几里得空间主要是定义了内积、距离、角（没错，就是初中的那些定义），理解了这些再去理解数学定义就很明确了。

B站视频资源-高等代数第九章：欧几里得空间

线性代数

图神经网络入门

1、GNN的发展

什么是图？
非欧几何与欧几里德几何区别为：几何结构不同、平行公理不同、创作者不同。

一、几何结构不同
1、非欧几何：非欧几何的几何结构是曲面的空间结构。
2、欧几里德几何：欧几里德几何的几何结构是平面的空间结构。

二、平行公理不同
1、非欧几何：非欧几何认为第五公设是不可证明的，并由否定第五公设的其他公理代替第五公设：过直线外一点至少存在两条直线和已知直线平行。

# 五大公设 现代版本
以下是欧几里得的五大公设：
公设一：任两点必可用直线连接
公设二：直线可以任意延长
公设三：可以任一点为圆心，任意长为半径画圆
公设四：所有的直角皆相同
公设五（现在又称为平行公理）：过线外一点，恰有一直线与已知直线平行

【欧几里德几何（欧氏空间）的第五公设：过直线外一点，有且只有一条直线与已知直线平行】

# 五大公设 原始版本
在《几何原本》一开始，欧几里德就开门见山地给出了23个定义，5个公设，5个公理。其实他说的公设就是我们后来所说的公理，他的公理是一些计算和证明用到的方法（如公理1：等于同一个量的量相等，公理5：整体大于局部等）他给出的5个公设倒是和几何学非常紧密的，也就是后来我们教科书中的公理。分别是：
公设1：任意一点到另外任意一点可以画直线
公设2：一条有限线段可以继续延长
公设3：以任意点为心及任意的距离可以画圆
公设4：凡直角都彼此相等
公设5：同平面内一条直线和另外两条直线相交，若在某一侧的两个内角和小于二直角的和，则这二直线经无限延长后在这一侧相交。（说明 这就是著名的第五公设，它与“直线外一点只能引一条直线与已知直线平行”是等价的，所以又有“平行公设”之称。）

《几何原本》中的公理亦共有5条：
公理1 等于同量的量相等。
公理2 等量加等量，其和相等。
公理3 等量减等量，其差相等。
公理4 能迭合的量一定相等。
公理5 整体大于部分。
欧几里德是这样区分公理与公设的：
第一，公理适合于一切科学，而公设是几何所特有的；
第二，公理本身是自明的，公设没有公理那样自明，但也是不加证明而承认其真实性的。
时至今日，人们已不在区分公理与公设了，都用公理一词来表明。

2、欧几里德几何：欧几里德几何提出平行公理：过直线外一点有且只有一条直线与已知直线平行。

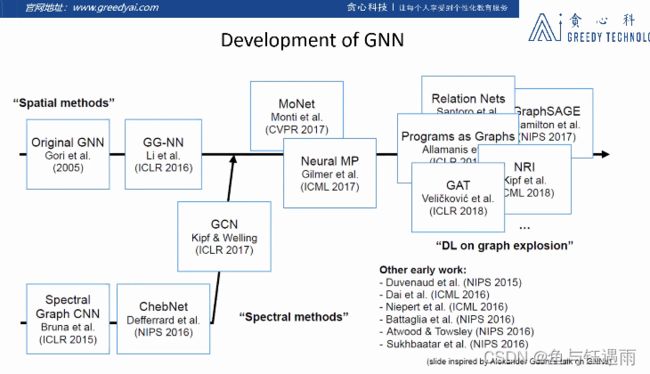
图神经网络的概念，最早是在2005年提出来的，在2005年概念的基础之上，有一位博士在2015年，将整个的概念放到了自己的博士论文中，一定程度上定义了图神经网络基础的结构。
最早的图神经网络是在空间域的角度被提出来的，这些图神经网络主要被用来做分子结构的分析，或者说试图去解决一些数学里面的图论问题。由于很多场景都可以转换为我们刚才所说的图结构，所以说使用图神经网络来建模，还是非常有前途的。
以至于说是在2009年之后，图神经网络这个领域也会有一些进阶的研究，但是没有太大的突破性的进展。直到2015年，或者说从2013年开始，在图信号处理这样一门学科的基础上，Lecun的一名学生，在自己的文章中提出了在频域上（图信号）上的卷积神经网络，他们从信号处理的角度，重新定义了一套在图信号上的傅立叶变换形式，并且他们基于信号处理中一些卷积的概念，提出了在图信号中一些卷积的概念，在这个理论的基础上就有了后面不同卷积核（ChebNet)的图卷积神经网络。

再到后来，到了2017年，Welling这个大佬，他试图将频域角度和空间域角度的两种卷积模型给结合起来，他告诉我们事实上，从这两个角度开发出来的文章，从理论或者模型上来说是等价的。
自有了2017年这项工作之后，后续的工作主要是在空间域这个角度展开了，一定程度上我们在空间域展开的模型它更容易建模实现和理解。

随着神经网络的兴起，在2015年左右，逐渐发现神经网络的功能的强大，就出现了各种各样不同的变种，比较流行的有GraphSAGE和GAT。这些网络也有了很大的应用。
其实还需要提到另外一个重要的点，在2015年左右NLP领域中word2Vec这样一个想法的启发下，我们在图数据上的表示学习其实也逐渐地兴起，表示学习可以说是和图神经网络比较平行的一个学科。主要目的是学习图节点的一个更好的表示。
上面这个图就概括了图神经网络大体的发展过程，我们发现说，我们可以有两个角度来审视这些网络。一个是所谓的空间域的角度，一个是所谓的频域的角度。这也是这次公开课我们想要去了解的两个。

2、空间域（GNN）图卷积

我们认为这是最早的空域GNN的起源文献，是Franco大佬的博士论文。最早期图神经网络的基本定理是基于不动点定理，这种神经网络是这样考虑的：假设我们输入的是一张图，我们这张图里的每一个节点都有自己的特征，自己的Feature，每一条边也都有自己的特征。具体这些特征表示什么，主要取决于我们的应用了。最早期图神经网络的学习目标是获得每一个节点的隐藏状态，或者说获得每一个节点隐状态的表示。我们可以记为第一个节点最后的隐藏状态表示为$x_1$以此类推。最终我们想要学到的是给每一个节点都学习得到一个隐状态表示，我们的要求就是在隐状态的表示里面，它可以表征整个图的结构，就相当于整个图的链接关系它都可以反映在它的隐状态表示里面。那如何让每一个节点都感知到图上的其他节点呢？就是说我们如何在每一个隐状态表示上，去感知到其他节点的特征呢？这就涉及到图神经网络的最早期的GNN的一个大体的思想，他们的思想就是说，我们尝试使用迭代更新的方式来去得到所有节点的一个隐状态的表示。

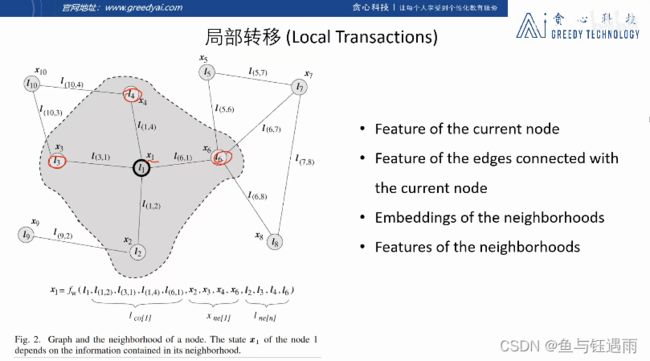
迭代就是，我们使用更新函数更新每个节点的隐状态，我们的更新然后一般会接受四部分的输入作为自己的输入，

• 当前节点的特征
• 和当前节点相连的边的特征
• 相邻节点的特征（features）
• 每一个邻居节点当前的隐状态（表示向量embedding)

每一个节点的更新函数都是贡献的，我们通过神经网络拟合这个更新的函数的话，就变成了图神经网络了。
我们假设，随着迭代更新，我们能够在节点的隐表示上获得其相邻节点的信息（包括结构信息和特征信息）。第一步更新可以看到与它距离为1的节点，第二步更新可以看到与他距离为2的节点。因此迭代次数越多，越有机会感知到整张图。

除此之外呢，我们可以在图卷积神经网络中，得到了隐表示，如何将他们应用到下游任务中（节点分类、边分类或边预测、整张图的分类）呢，我们还需要另外的函数：局部输出函数

在图神经网络中，会用神经网络的方法来建模更新函数f和局部输出函数g

例如下图：蛋白质活性分类

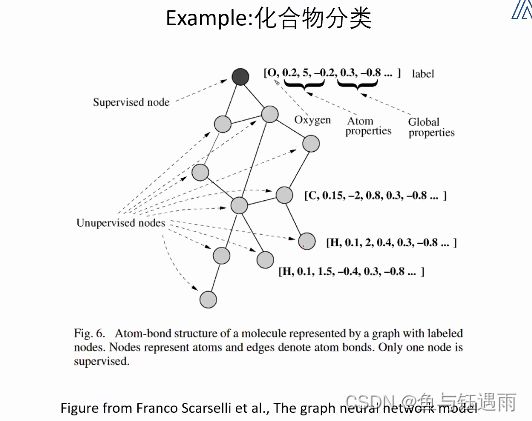
那如何选取一个合适的G函数呢？ 大概有两个套路：

1. 我们可以选定一个特定的节点，所有的监督都是加在这个节点上的。
2. 尝试构造一个和图上所有节点都相连的伪节点，最后使用伪节点它所对应的表示来加入监督。

采用那种方式，取决于任务。

过程中有一个问题，我们怎么能保证这个迭代过程是收敛的呢？

因为明显的你不知道它最后迭代几步后可以收敛，最后这个图神经网络停止迭代的原则是说，节点的隐表示不怎么变动。那最原始的这套GNN为什么能够收敛呢？这套方法，是根据巴拿赫不动点定理建立起来的。
这个不懂点定理告诉我们，如果我们可以给局部转移函数f加上一些限定的话，我们就可以保证在迭代的操作下，可以得到稳定的解。那定义什么样的限定呢？ 这个定理告诉我们，我们需要将$f$定义成一个压缩映射。
什么是压缩映射？ 我们认为$F(x)$是一个映射，可以把集合中的一个元素映射为另外一个集合的元素。如果我们能保证映射后两个点的距离，小于映射前，我们就认为这个映射是压缩映射。巴拿赫不动点定理的内容就是，如果我们能够保$F$是一个压缩映射，那我们就能保证通过不断的迭代，最终能够将函数结果收敛到特定的点。这一套理论是有证明的，但是我们直接拿来用就可以了。

那我们如何在具体实现中加入限定呢？
我们刚才说了，局部转移函数我们可以把它实现成神经网络（例如一个简单的前馈神经网络），那如何保证它是一个压缩映射呢？（映射后的距离：欧氏距离，比原来要小）我们可以对F函数进行一些限制。
通过一定的推导我们可以知道说，如果我们可以限制F映射的雅可比矩阵的大小，那么我们就能够限制F的映射是一个压缩映射，一般情况下，在最原始的图神经网络上，我们会对F映射函数对应的雅可比矩阵进行一个惩罚项，相当于我们把它限制成一个特定的大小C，我们在节点的监督上加上惩罚项，试图强制使得F这个映射是一个压缩映射，只有在这种情况下，我们才能保证最原始的图卷积神经网络的迭代最终是收敛的，可以收敛到一个点。

那么上面最初代的图神经网络GNN，确实能解决问题，但是它有一个致命的缺陷-过平滑（过拟合）

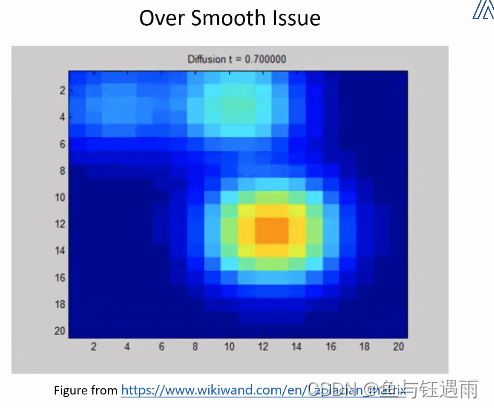
随着迭代次数的增加，节点的隐表示会逐渐同质化，无法分辨了。这样我们就无法识别每个节点的区别了（分类了）。

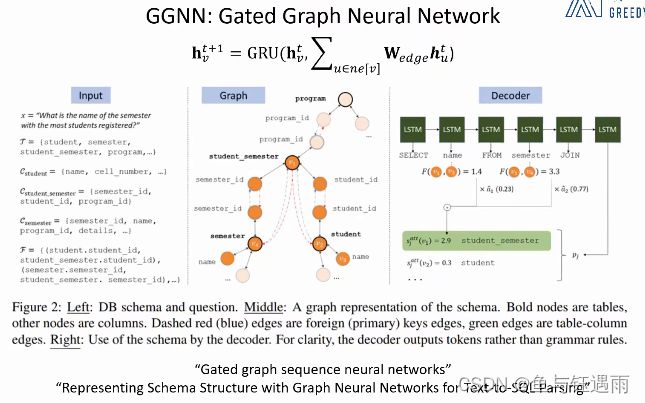
有的学者发现，早期的神经网络的迭代更新过程像是循环神经网络，因此提出了GGNN，对GNN进行了改进，用循环神经网络中的GRU单元去替换之前的F激活函数（局部转移函数），并且在这个神经网络中，不再要求F是压缩映射，也不再要求迭代到收敛之后再把隐特征应用到下游任务中去，迭代特定的步长就停止。简单粗暴的通过提前停止迭代的过程，使得每一个节点是有一定区别的。还有一些其他细节的区别。最重要的区别，就是不再要求压缩映射和更新到收敛才能去做下游任务。

在GGNN的基础上，就有了后来的图卷积神经网络，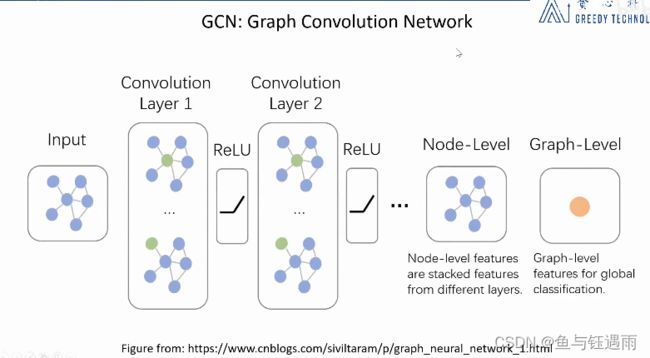
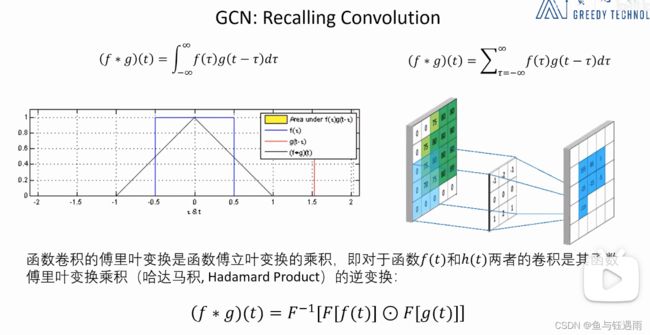
一定程度上，GCN的套路和最开始的GNN的套路很像，基本都是一样的，GCN摆脱了循环的方式，开始尝试学习图像中的卷积神经网络的想法，使用分层的思路，在每次更新节点的隐状态的时候，使用一个特定的函数，然后我们把这一个函数认为是这一层的操作算子或者说卷积算子，然后我们去堆叠不同的操作，我们把每一个操作都认为是不同的层，每一层做的也就是根据邻居节点更新中心节点的隐表示。具体实现的时候，就用神经网络写代码实现，比如说一个线性变换+一个非线性激活。区别于GNN，GCN的每一层可以用不同的更新函数不要求共享参数，同时无需迭代。

不同的更新函数实现的方式，能够创造不同的模型：比如说用attention的方式，就创造了GAT。
从理念上来看，空域卷积和深度学习中图像上的卷积应用方式很像，空域GNN的核心就在于聚合邻居节点的信息。
有了这种思路之后，就有人想把这种思路用统一的框架描述出来，就有了MPNN（空域卷积形式化的框架）。

它把空域卷积分为两部分：消息传递$M函数$和消息更新$U函数$。

定义在MPNN消息传递这一框架下的模型都有一个缺陷，卷积操作针对的对象，其实是整张图，要卷积，我们就要对每一个节点都进行卷积，更新每一个节点的状态。在进行计算的时候，需要将每一个节点都放到显存或者内存里面，而事实上，在实际的应用场景中我们发现，这个不现实。

随后有人提出了GraphSage的改进（采样和聚合），既然节点多，我们不用全部邻居来更新，而是先采样部分邻居，然后再更新。（如何去sampling和aggregate就是我们需要自行定义的事情），实验表明在保证精度的情况下，graphsage可以降低时间和空间复杂度。

GAT就是通过特殊的方式来定义聚合（局部更新）函数，一种attention的方式。这种思想引自NLP领域。而这种对邻居可学习加权聚合的方式，十分的流行，以至于GAT目前占据了大部分空域图神经网络。

为什么叫空域卷积？ 通过链接关系更新（聚合）隐表示的方式，就叫做空域卷积。

注意：特征随机初始化是可以尝试的，因为我们可以认为在迭代的过程中GNN或者GCN能够学到一个好的特征表示。

频谱域（频域）卷积

先学习一些常见的定义
拉普拉斯矩阵：描述图中节点之间的邻接关系。 一般是由图的邻接矩阵和度矩阵定义出来的。

这样定义出的拉普拉斯矩阵具有很多很好的性质：
1、是对称矩阵，可以进行特征分解
2、只有在中心节点和一阶相邻节点的对应元素位置是非0，其余都是0
3、图上的拉普拉斯矩阵的定义可以和信号处理中的拉普拉斯算子进行类比

注意：谱分解又叫特征分解、对角化。
一个矩阵如果可以写成1式三个矩阵相乘的形式，我们就称其可以特征分解。
U是正交矩阵，它的$U^{-1}=U^T$
中间的是对角矩阵。
其实，并不是所有的矩阵都可以做特征分解，有一个充要条件：如果一个矩阵是n阶方阵，并且存在n个线性无关的特征向量，<=>它就可以进行特征分解。
而恰好定义的拉普拉斯矩阵是一个半正定的对称特征矩阵，它一定可以做特征分解。并且我们可以保证该对称矩阵有n个线性无关的特征向量，它的特征值一定是非负的，且最小的特征值是0.

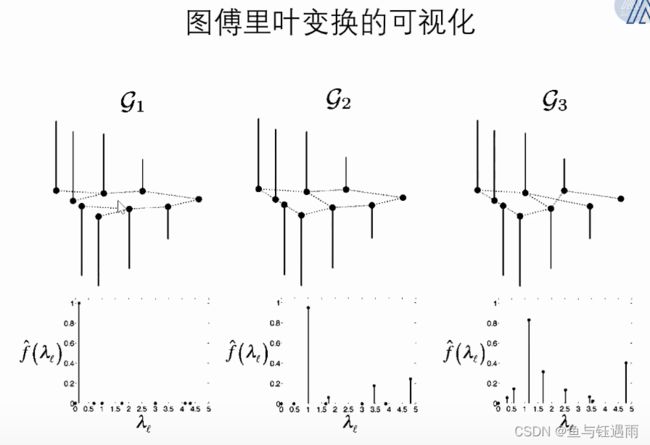
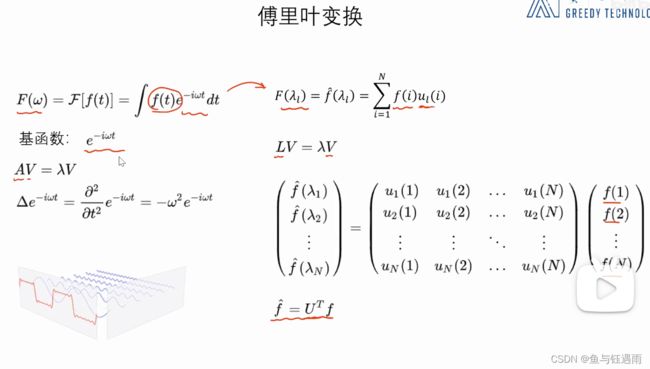
左侧是《复变函数》这门课里面所讲的傅立叶变换的形式，右边是类比到graph中的形式。
傅立叶变换：使用一组基函数的线性组合来表示原来的函数。我们把基函数的系数认为是原始函数经过傅立叶变换之后的结果。
这个基函数，是拉普拉斯算子的特征函数（类似于特征向量，对应的常数是特征值？个人理解）。
$A$拉普拉斯算子的特征函数， $V$函数。
有了特征函数，就能定义出基函数，这样就有了图上的傅立叶变换。
拉普拉斯矩阵就相当于图信号上的拉普拉斯算子。$U$是由拉普拉斯算子（拉普拉斯矩阵）的特征向量（是列向量）组成的矩阵。