【论文】解读AM-GCN: Adaptive Multi-channel Graph Convolutional

解读AM-GCN: Adaptive Multi-channel Graph Convolutional

摘要

当下提出的新问题：GCNs能否可以在信息丰富的复杂图中优化集成节点的特征喝拓扑结构。提出实验研究。(whether GCNs can optimally integrate node features and topological structures in a complex graph with rich information.)结果表明，最新的GCNs在融合节点特征和拓扑结构上(in fusing node features and topological structures)的功能与最佳或者令人满意的结果相距甚远。

问题描述：这个弱点可能会严重阻碍分类神经网络在某些任务中的能力，因为分类神经网络可能无法自适应地学习拓扑结构和节点特征之间地一些深度相关信息。希望提出新型的GCNs可以保留最新进GCNs的优势又融合拓扑结构和节点特征的能力。

新结构：用于半监督分类的自适应多通道图卷积网络
核心思想：同时从节点特征、拓扑结构及其组合总提取特定和常见的嵌入，并适应注意机制来学习嵌入的自适应重要性权重。(the central idea is that we extract the specific and common embedding s from node features,topological structures ,and their combinations simultaneously, and use the attention mechanism to learn adaptive importance weights of the embeddings.)
代码链接：点这里

1. introduction

网络数据（network data)无处不在.GCNs是用于学习图形数据(graph data)的神经网络。用于解决 节点分类(node classification), 图分类(graph classification), 链接预测(link prediction), 推荐(recommendiation)

GCN及其变体¹通常遵循消息传递²的方式。一个关键步骤是特征聚合，即一个节点在每个卷积层中聚合来自其拓扑邻居的特征信息。这样，特征信息通过网络拓扑传播到节点嵌入，然后这样学习的节点嵌入被用于分类任务。整个过程由节点标签部分监督。GCN的巨大成功部分归功于GCN提供了一种基于拓扑结构和节点特征的融合策略来学习节点嵌入，并且融合过程由端到端的学习框架来监督。

最先进的GCN 在 fusing node features and topological structures的弱点。

• 文献 Li提出 GCNs实际上是对节点特征进行拉普拉斯平滑，使整个网络中的节点嵌入逐渐收敛。
• 文献Nt and Maehara 和文献 Wu 证明了当特征信息在网络拓扑结构上传播时，拓扑结构对节点特征起到**低通滤波(low-pass filtering)**的作用
• 文献Gao设计了在GCN设计一个条件随机场(CRF)层(Conditional Random Field)，以明确保持节点之间的连通性

思考：gcn真正从拓扑结构和节点特征中学习融合的是什么信息？

作为这项研究的第一个贡献，我们提出了实验，评估GCNs在融合拓扑结构和节点特征的的能力。

令人惊讶的是，我们的实验清楚地表明，在网络拓扑结构和节点特征上的融合能力明显远离最优甚至令人满意。即使在节点特征/拓扑与节点标签之间的相关性非常清楚的一些简单情况下，GCNs仍然不能充分融合节点特征和拓扑结构来提取最相关的信息(如第2节所示)。这种弱点可能会严重阻碍分类网络在某些分类任务中的能力，因为分类网络可能无法自适应地学习拓扑结构和节点特征之间的一些相关信息。

思考：我们能否弥补这一弱点，设计一种新型的通用通信网络，既能保留最先进的通用通信网络的优点，同时又能大大增强融合拓扑结构和节点特征的能力？”
分析：GCN的优势在于良好的融合能力可以为分类任务充分提取和融合最相关的信息。当下的挑战是网络数据(network data)和分类任务(classification task)之间的关联复杂不可知。分类可以与拓扑（topology)、节点特征(node features)、及他们的组合相关联。
提出AM-GCN，中心思想为：同时基于节点特征、拓扑结构及其组合来学习节点嵌入；基本原理为：特征之间的相似性和由拓扑结构推断的相似性是相互补充的，并且可以自适应地融合以导出用于分类任务的更深的相关信息。

技术上，为了充分利用特征空间中的信息，我们将节点特征生成的k近邻图作为特征结构图(feature structural graph)。利用特征图(feature graph)和拓扑图(topology graph)，我们在拓扑空间和特征空间上传播(动词)节点特征，从而用两个特定的卷积模块在这两个空间中提取两个特定的嵌入。考虑到两个空间之间的共同特征，我们设计了一个具有参数共享策略的共同卷积模块，用于提取两个空间共享的共同嵌入。我们进一步利用注意机制来自动学习不同嵌入的重要性权重，以便自适应地融合它们。这样，节点标签能够监督学习过程，自适应地调整权重以提取最相关的信息。此外，我们还设计了一致性和差异约束，以保证学习嵌入的一致性和差异。

主要贡献如下：

• 我们提出了实验，评估融合拓扑结构和节点特征的全球合作网络的能力，并确定GCN的弱点。我们进一步研究了重要的问题，即如何大幅度提高GCN分类的融合能力。
• 我们提出了一种新的自适应多通道GCN框架，AM-GCN，它在拓扑和特征空间上执行图形卷积运算。结合注意机制，可以充分融合不同的信息。
• 我们在一系列基准数据集上的大量实验清楚地表明，AM-GCN优于最先进的GCNs，并且从节点特征和拓扑结构中很好地提取了最相关的信息，用于具有挑战性的分类任务。

2. FUSION CAPABILITY OF GCNS: AN EXPERIMENTAL INVESTIGATION

GCNS聚变能力的实验研究
在本节中，我们使用两个简单而直观的案例来检验最先进的GCNs是否能够自适应地从图中的节点特征和拓扑结构中学习，并将其充分融合以用于分类任务。主要思想是，我们将分别清楚地建立节点标签与网络拓扑和节点特征之间的高度相关性，然后我们将检查GCN在这两种简单情况下的性能。具有良好融合能力的GCN应在节点标签的监督下自适应提取相关信息，以提供良好的结果。然而，如果性能与基线相比急剧下降，这将表明GCN不能自适应地从节点特征和拓扑结构中提取信息，即使节点特征或拓扑结构与节点标签之间存在高度相关性。

2.1 Case 1: Random Topology and Correlated Node Features

我们生成一个由900个节点组成的随机网络，其中任意两个节点之间建立边的概率为0.03。每个节点有一个50维的特征向量。为了生成节点特征，我们将3个标签随机分配给900个节点，对于具有相同标签的节点，我们使用一个高斯分布来生成节点特征。三类节点的高斯分布具有相同的协方差矩阵，但是三个不同的中心彼此远离。在该数据集中，节点标签与节点特征高度相关，但与拓扑结构不相关。

我们用GCN [14]来训练这个网络。对于每个类，我们随机选择20个节点用于训练，另外200个节点用于测试。我们仔细调整超参数，以报告最佳性能并避免过度平滑。此外，我们仅将MLP(多层感知机) [21]应用于节点特征。GCN和MLP的分类准确率分别为75.2%和100%。

结果符合预期。由于节点特征与节点标签高度相关，因此MLP表现出优异的性能。GCN从节点特征和拓扑结构中提取信息，但不能自适应地融合它们以避免拓扑结构的干扰。它比不上MLP的高性能。

2.2 Case 2: Correlated Topology and Random Node Features

我们生成另一个有900个节点的网络。这一次，每个50维的节点特征是随机生成的。为了拓扑结构，我们使用随机块模型(SBM) (Stochastic Blockmodel )[12]将节点分成3个社区(节点分别为0-299、300-599、600-899)。在每个社区内，建立边的概率设置为0.03，不同社区的节点之间建立边的概率设置为0.0015。在该数据集中，节点标签由社区确定，即同一社区中的节点具有相同的标签。

我们再次将GCN应用于这个网络。我们还将DeepWalk[22]应用于网络拓扑，即DeepWalk忽略的特征。GCN和DeepWalk的分类准确率分别为87%和100%。

DeepWalk表现良好，因为它对网络拓扑结构进行了全面建模。GCN从节点特征和拓扑结构中提取信息，但不能自适应地融合它们以避免节点特征的干扰。跟DeepWalk的高性能没法比.

总结:这些案例表明，GCN [14]目前的聚变机制远非最佳，甚至不能令人满意。即使节点标签与网络拓扑或节点特征之间的相关性很高，当前的GCN也不能充分利用节点标签的监督自适应地提取最相关的信息。然而，现实中的情况更加复杂，因为很难知道拓扑或节点特征是否与最终任务更相关，这促使我们重新思考GCN的当前机制。

3. AM-GCN: THE PROPOSED MODEL

问题设置：我们主要研究属性图$G=(A,X)$的半监督节点分类，where $A\in R^{N\times N}$是有$n$个节点的对称邻接矩阵(symmetrica asjacency matrix)，$X\in R^{n\times d}$是节点特征矩阵(node feature matrix),$d$是节点特征的维数。特别的，$A_{ij}=1$表示节点$i$和$j$之间有一条边(edge);否则，$A_{ij}=0$。我们假设每个节点属于$C$个类别(classes)的一个.

AM-GCN的总体框架如图1所示。其核心思想是AM-GCN允许节点特征不仅在拓扑空间中传播，而且在特征空间中传播，并且与节点标签最相关的信息应该从这两个空间中提取。为此，我们 构建了基于节点特征$X$的特征图。 然后，通过两个特定的卷积模块，节点特征$X$能够在特征图和拓扑图上传播，以分别 学习两个特定的嵌入$Z_F$和$Z_T$。此外，考虑到这两个空间中的信息具有共同的特征，我们设计了一个具有参数共享策略的共同卷积模块来 学习共同嵌入的$Z_{CF}$·和$Z_{CT}$，并且采用了一致性约束(consistency constraint)${\mathcal{L}}_c$来增强$Z_{CF}$和$Z_{CT}$的“共同”性质。此外，还有一个差异约束(disparity constraint)${\mathcal{L}}_d$，以确保$Z_F$和${}_{Z}CF$以及$Z_T$和$Z_{CT}$之间的独立性。考虑到节点标签可能与拓扑或特征或两者相关，AM-GCN利用注意机制自适应地将这些 嵌入与学习到的权重融合，以便为最终的分类任务提取最相关的信息Z。

3.1 Specific Convolution Module

捕捉

图卷积

图卷积

structure of nodes in feature space

feature graph

topology graph

嵌入表示1

嵌入表示2

捕捉方法： 基于节点的特征矩阵$X$,建立 k-nearest neighbor(kNN) graph$G_f=(A_f,X)$.where $A_f$是kNN图的邻接矩阵。

流程：
1）首先计算$n$个节点的相似矩阵(similarity matrix)$S\in R^{n\times n}$。列举两种方法获得相似矩阵，节点$i$和节点$j$的特征向量为$X_i$和$X_j$.

• Cosine Similarity(余弦相似性)
  $$S_{ij}=\frac{X_i\cdot X_j}{|X_i||X_j|}\text{\hspace{1em}(1)}$$
• Heat Kernel热核,设置$t=2$
  $$S_{ij}=e^{-\frac{||X_i-X_j|{|}^2}{t}}\text{\hspace{1em}(2)}$$

2） 特征图上的卷积模块

• input：$(A_f,X)$
• l-th layer output$$Z_f^{(l)}=ReLU({\tilde{D}}_f^{-1/2}{\tilde{A}}_f){\tilde{D}}_f^{-1/2}{Z}_f^{(l-1)}{W}_f^{(l)}\text{\hspace{1em}(3)}$$
  where $W^{(l)}$是GCN的l-th的权重矩阵，ReLU是激活函数，初始化$Z_f^{(0)}=X$
  specifically,${\tilde{A}}_f=A_f+I_f$,${\tilde{D}}_f$是${\tilde{A}}_f$的对角度矩阵。
• output:$Z_F$ 得到嵌入表示

3） 拓扑图上的卷积模块

• input:$G_t=(A_t,X_t)原始输入图，where $A_t=A$,$X_t=X$
• 卷积层：同上
• output:$Z_T$得到嵌入表示

3.2 Common Convolution Module

公共卷积模块
实际上，特征空间和拓扑空间并不是完全不相关的。基本上，节点分类任务可能与特征空间或拓扑空间或两者中的信息相关联，这很难事先知道。因此，我们不仅需要提取这两个空间中的节点特定嵌入，还需要提取这两个空间共享的公共信息。这样，任务将变得更加灵活，以确定哪部分信息最相关。为了解决这个问题，我们设计了一个带参数共享策略的共GCN算法，使嵌入在两个空间共享。
1） 用Comon-GCN从topology graph$(A_t,X)$抓取节点嵌入$Z_{ct}^{(l)}$
$$Z_{ct}^{(l)}=ReLU({\tilde{D}}_t^{-1/2}{\tilde{A}}_t){\tilde{D}}_t^{-1/2}{Z}_t^{(l-1)}{W}_c^{(l)}\text{\hspace{1em}(4)}$$
where $W_c^{(l)}$是Common-GCN 的 l-th 层的权重矩阵，$Z_{ct}^{(l-1)}$是$(l-1)$层的节点嵌入，$Z_{ct}^{(0)}=X$
2） 用Common-GCN从feature graph $(A_f,X)$抓取节点嵌入$Z_{cf}^{(l)}$
$$Z_{cf}^{(l)}=ReLU({\tilde{D}}_f^{-1/2}{\tilde{A}}_f){\tilde{D}}_f^{-1/2}{Z}_f^{(l-1)}{W}_c^{(l)}\text{\hspace{1em}(5)}$$
where,注意到公用一个权重矩阵$W_c^{(l)}$
3） 两个空间的公共嵌入
$$Z_C=(Z_{CT}+Z_{CF})/2\text{\hspace{1em}(6)}$$
where,$Z_{CT}$和$Z_{CF}$分别是不同图输入的最终输出嵌入。

3.3 Attention Mechanism

当下有两个特定的嵌入$Z_T$和$Z_F$和一个公共嵌入$Z_C$,使用注意力机制学习相应的重要性：
$$({\alpha }_t,{\alpha }_c,{\alpha }_f)=att(Z_T,Z_C,Z_F)\text{\hspace{1em}(7)}$$
here,${\alpha }_t,{\alpha }_c,{\alpha }_f\in R^{n\times 1}$分别是$Z_T,Z_C,Z_F$的$n$个节点的注意值

关注节点$i$,它在$Z_T$的嵌入是$Z_T^i\in R^{1\times h}$(即，$Z_T$的第$i$行）
1)首先我们使用一个非线性变换将嵌入变换,再使用一个共享的注意力向量$q\in R^{h^{\prime }\times 1}$得到注意力值$w_T^i$:
$$w_T^i=q^T\cdot tanh(W\cdot (Z_T^i{)}^T+b)\text{\hspace{1em}(8)}$$
here,$W\in R^{h^{\prime }\times h}$是权重矩阵，$b\in R^{h^{\prime }\times 1}$是偏置向量。
同理，得到注意力值$w_C^i$,$w_F^i$
2）使用softmax函数对注意力值归一化
$${\alpha }_T^i=softmax(w_T^i)=\frac{exp(w_T^i)}{exp(w_T^i)+exp(w_C^i)+exp(w_F^i)}\text{\hspace{1em}(9)}$$
${\alpha }_T^i$的值越大对应的嵌入则更重要。${\alpha }_C^i$，${\alpha }_F^i$同理。

对所有的$n$个节点,有学习权重${\alpha }_t=[{\alpha }_T^i],{\alpha }_c=[{\alpha }_C^i],{\alpha }_f=[{\alpha }_F^i]\in R^{n\times 1}$,表示为${\alpha }_T=diag({\alpha }_t),{\alpha }_C=diag({\alpha }_t),{\alpha }_F=diag({\alpha }_f)$

3）组后结合这三种嵌入得到最终的嵌入$Z$:
$$Z={\alpha }_T\cdot Z_T+{\alpha }_C\cdot Z_C+{\alpha }_F\cdot Z_f\text{\hspace{1em}(10)}$$

3.4 Objective Function

3.4.1 Consistency Constraint.

对于Common-GCN的两个输出嵌入$Z_{CT}$和$Z_{CF}$,尽管有共享的权重矩阵,还是设计了一个一致性约束,来进一步增强其通用性。
1）用$L_2-normalization$去对嵌入矩阵标准化为$Z_{CTnor}$,$Z_{CFnor}$
2） 用标准化后的矩阵去捕捉$n$个节点的相似性表示为$S_T$和$S_F$:
$$\begin{array}{r}{S}_T=Z_{CTnor}\cdot Z_{CTnor}^T\\ S_F=Z_{CFnor}\cdot Z_{CFnor}^T\end{array}\text{\hspace{1em}(11)}$$
3） 产生相似性约束(因为一致性意味着两个相似性矩阵应该是相似的)
$${\mathcal{L}}_c=||S_T-S_F|{|}_F^2\text{\hspace{1em}(12)}$$

3.4.2 Disparity Constraint

因为$Z_T$和$Z_{CT}$都是来子相同的图$G_t=(A_t,X_t)$,为了确保捕捉不同的信息，我们使用 **Hibert-Schmidt Independence Criterion(HSIC)**一种简单但有效的独立性度量，来增强这两种嵌入的差异.因此，
1） $Z_T$和$Z_{CT}$的HSIC约束定义为：
$$HSIC(Z_T,Z_{CT})=(n-1{)}^{-2}tr(R{K}_{T}R{K}_{CT})\text{\hspace{1em}(13)}$$
where,$K_T$和$K_{CT}$是Gram 矩阵 with $k_{T,ij}=k_T(Z_T^i,Z_T^i)$和$k_{CT,ij}=k_T(Z_{CT}^i,Z_{CT}^i)$
$R=I-1/ne{e}^T$,where $I$是一个单位矩阵，$e$是全1列向量。
$K_T$和$k_{CT}$是内积核函数。
2） 同理，对于嵌入$Z_F$和$Z_{CF}$有约束定义为：
$$HSIC(Z_F,Z_{CF})=(n-1{)}^{-2}tr(R{K}_{F}R{K}_{CF})\text{\hspace{1em}(14)}$$
3） 设置差异约束
$${\mathcal{L}}_d=HSIC(Z_T,Z_{CT})+HSIC(Z_F,Z_{CF})\text{\hspace{1em}(15)}$$

3.4.3 Optimization Objective

我们使用的公式（10）中的输出嵌入$Z$是具有线性变换核softmax函数的半监督分类任务的结果。将$n$个节点的分类预测表示为$\hat{Y}=[{\hat{y}}_{ic}]\in R^{n\times C}$,where ${\hat{y}}_{ic}$是节点$i$属于 类别 c的概率。$\hat{Y}$可以被计算：
$$\hat{Y}=softmax(W\cdot Z+b)\text{\hspace{1em}(16)}$$
where,$softmax(x)=\frac{x}{{\sum }_{c=1}^{C}exp(x_c)}$是对所有类别的标准化。

假设训练集设为$L$,对 each $l\in L$的真实标签是$Y_l$,预测标签是$hat{Y}_l$.所有训练节点上的节点分类的交叉熵损失表示为${\mathcal{L}}_t$:
$${\mathcal{L}}_t=-\sum _{l\in L}\sum _{i=1}^C{Y}_{li}lin{\hat{Y}}_{li}\text{\hspace{1em}(17)}$$
结合节点分类任何核约束，最后的目标函数为：
$$\mathcal{L}={\mathcal{L}}_t+\gamma {\mathcal{L}}_c+\beta {\mathcal{L}}_d\text{\hspace{1em}(18)}$$
where,$\gamma$和$\beta$是移植性约束和差异性约束项的参数。在标记数据的指导下，我们可以通过反向传播来优化所提出的模型，并学习用于分类的节点的嵌入。

4 EXPERIMENTS

4.1 Experimental Setup

数据集:我们提出的AM-GCN是在六个真实世界的数据集上进行评估的，这些数据集总结在表1中，此外，我们在补充中提供了所有的数据网站，以保证再现性。

Baselines： 我们比较了AM-GCN和两种现有的方法，包括两种网络嵌入算法和六种基于图形神经网络的方法。此外，我们在补充中提供了所有的代码网站，以供复制。

Parameters Setting： 为了更全面地评估我们的模型，我们为训练集选择了三个标签率(即每类20、40、60个标签节点)，并选择1000个节点作为测试集。所有基线都用他们论文中建议的相同参数进行初始化，我们还进一步小心地变换参数以获得最佳性能。
对于我们的模型，我们同时训练三个具有相同隐藏层维数(nhid1)和相同输出维数(nhid2)的2层GCNs，其中$nhid1\in \{512，768\}$和$nhid2\in \{32，128，256\}$。

我们用$0.0001\sim 0.0005$的学习率和Adam优化器。此外，dropout rate为0.5，weight decay $in\{5e-3,5e-4\}$和$k\in \{2,...,10\}$对于k-最近邻图。在$\{0.01，0.001，0.0001\}$和$\{1e-10，5e-9，1e-9，5e-8，1e-8\}$中搜索一致性系数约束和差异约束。

对于所有方法，我们使用相同的分区运行5次，并报告平均结果。我们使用准确性(ACC)和macro F1-score(F1)来评估模型的性能。为了再现性，我们在附录中提供了具体的参数值(第A.3节)。

4.2 Node Classification

节点分类结果见表2，其中L/C表示每类标记节点数。我们观察到以下情况:

• 与所有基线相比，所提出的AM-GCN总体上在所有标签率的所有数据集上实现了最佳性能。特别是对于ACC，AM-GCN在BlogCatalog上实现了8.59%的最大相对改进，在Flickr上实现了8.63%的最大相对改进。结果证明了AM-GCN的有效性。
• 在所有数据集上，AM-GCN始终优于GCN和kNN-GCN，这表明了AM-GCN自适应融合机制的有效性，因为它可以提取比仅分别执行GCN和kNNGCN更多的有用信息。
• 通过与GCN和kNN-GCN的比较，我们可以发现拓扑图和特征图之间确实存在结构上的差异，在传统的拓扑图上执行GCN并不总是比在特征图上显示出更好的结果。比如在BlogCatalog、Flickr、UAI2010中，特征图的表现要比拓扑好。这进一步证实了GCN引入特征图的必要性。
• 此外，与GCN相比，AM-GCN在特征图(kNN)较好的数据集(如UAI2010、BlogCatalog、Flickr)上的改进更为显著。这意味着AM-GCN引入了一个更好更合适的kNN图作为标签来监督特征传播和节点表示学习。

4.3 Analysis of Variants

在本节中，我们将AM-GCN及其三个变体在所有数据集上进行比较，以验证约束的有效性。

• AM-GCN-w/o:AM-GCN 没有两个约束
• AM-GCN-c:AM-GCN带有一致性约束${\mathcal{L}}_c$
• AM-GCN-d:AM-GCN带有差异约束${\mathcal{L}}_d$

从图2的结果中，我们可以得到以下结论。
1）AM-GCN的结果始终是优于其他三个变体，表明将这两个约束结合使用的有效性。
2）在所有标签率数据集上,AM-GCN-c 和AM-GCN-d的结果通常优于AM-GCN-w/o,以验证了这两个约束的有效性。
3） 在所有数据集上，AM-GCN-c总体上优于AM-GCN-d,这意味着一致性约束在框架中起着更重要的作用。
4） 比较fig2 和tab2的结果，我们可以发现AM-GCN-w/o仍然获得了与基线相比非常有竞争力的性能，这表明我们的框架是稳定和有竞争力的。

4.4 Visualization

为了更直观的比较和进一步展示我们提出的模型的有效性，我们在BlogCatalog数据集上进行可视化任务。我们使用在softmax之前的最后一层AM-GCN(或GCN，GAT)上的输出嵌入，然后使用t-SNE绘制测试集的学习嵌入[26]。图3中BlogCatalog的结果是用真实标签着色的。

从图3中，我们可以发现DeepWalk、GCN和GAT的结果并不令人满意，因为不同标签的节点混合在一起了。显然，AM-GCN的可视化表现最好，其中学习的嵌入具有更紧凑的结构、最高的类内相似性和不同类之间最清晰的明显边界。

4.5 Analysis of Attention Mechanism

为了研究我们提出的模型所学习的注意力值是否有意义，我们分别分析了注意力分布和注意力学习趋势。

Analysis of attention distributions.AM-GCN学会了两个特定的和一个共同的嵌入，每一个都与注意力值相关联。我们对所有具有20个标签率的数据集进行了注意力分布分析，结果如图4所示。我们可以看到，对于Citeseer、ACM、CoraFull，拓扑空间中特定嵌入的关注值大于特征空间中的值，共同嵌入的值介于两者之间。这意味着拓扑空间中的信息应该比特征空间中的信息更重要。为了验证这一点，我们可以在表2中的这些数据集上看到GCN的结果优于kNN-GCN。相反，对于UAI2010，BlogCatalog和Flickr，对比图4和表2，我们可以发现kNN-GCN比GCN表现更好，同时特征空间中特定嵌入的关注值也大于拓扑空间中的关注值。总之，实验表明，我们提出的AM-GCN能够自适应地为更重要的信息分配更大的关注值。

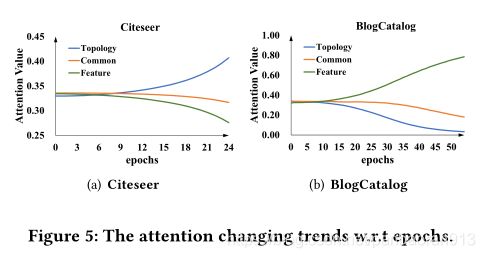
Analysis of attention trends我们分析了训练过程中注意力价值的变化趋势。这里我们以图5中带有20个标签率的Citeseer和BlogCatalog为例，其中x轴为epoch，y轴为average attention value。更多的结果在补充A.4.1中。在开始时，拓扑、特征和公共的平均注意力值几乎相同，随着训练时期的增加，注意力值变得不同。比如在BlogCatalog中，对于拓扑的关注值逐渐减少，而对于特征的关注值不断增加。这一现象与表2和图4的结论一致，即kNN-GCN带特征图 性能优于GCN，并且特征空间中的信息比拓扑空间中的信息更重要。我们可以看到，AM-GCN可以一步一步地学习不同嵌入的重要性。

4.6 Parameter Study

在这一节中，我们研究了Citeseer和BlogCatalog数据集上参数的敏感性。更多结果见A.4.2。

Analysis of consistency coefficient $\gamma$.我们测试了等式(18)中一致性约束权重$\gamma$的效果。从0到10000不等。结果如图6所示。随着一致性系数的增加，性能先上升后缓慢下降。基本上，当$\gamma$在所有数据集的$1e-4$到$1e+4$范围内时，AM-GCN是稳定的。我们还可以看到，20、40、60标签率的曲线显示出类似的变化趋势。

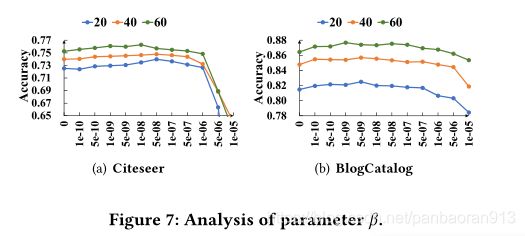
Analysis of disparity constraint coefficient $\beta$我们测试等式(18)中视差约束权重$\beta$的效果。并将其从0更改为$1e-5$。结果如图7所示。同样，随着$\beta$的增加，性能也先上升，但对于图7(a)中的Citeseer，如果$\beta$大于$1e-6$，性能会迅速下降，而对于BlogCatalog，性能相对稳定。

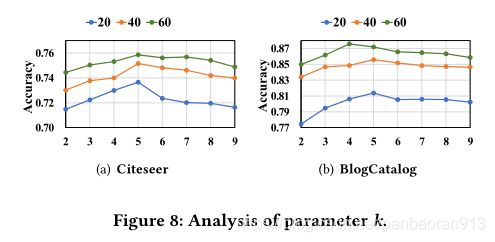
Analysis of k-nearest neighbor graph $k$/.为了检验kNN图中前k个邻域的影响，我们研究了图8中不同k值范围从2到10的AM-GCN的性能。对于Citeseer和BlogCatalog，精度先增加后开始降低。这可能是因为如果图形变得更密集，特征更容易被平滑，而且，更大的k可能会引入更多的噪声边缘。

5 RELATED WORK

最近，图卷积网络(GCN)模型[4，9，17，23，33，35]已被广泛研究。例如，[3]首先用图拉普拉斯算子设计了傅立叶域的图卷积运算。然后[5]进一步利用图拉普拉斯的切比雪夫展开来提高效率。[14]简化了卷积运算，并建议仅从一阶邻居中聚合节点特征。GAT [27]引入了注意机制，用学习到的权重来聚集节点特征。GraphSAGE [11]提出用均值/最大值/LSTM池从节点的局部邻域中采样和聚集特征。DEMO-Net [31]设计了一个感知度的特征聚合过程。MixHop [1]同时从网络每一层的一阶和高阶邻居中聚合特征信息。目前的大部分遗传神经网络本质上侧重于融合网络拓扑和节点特征来学习节点嵌入进行分类。此外，最近还有一些分析GCN融合机制的工作。例如，[15]表明GCNs实际上对节点特征执行拉普拉斯平滑，[20]和[30]证明拓扑结构对节点特征起低通滤波的作用。要了解更多关于GCNs的作品，请参考详细的评论[32，38]。然而，分类神经网络能否自适应地从节点特征和拓扑结构中提取相关信息进行分类仍不清楚。

6 CONCLUSION

在这篇文章中，我们重新思考了GCN的网络拓扑和节点特征的融合机制，令人惊讶地发现它远非最优。基于这个基本问题，我们研究了如何自适应地从拓扑和节点特征中学习最相关的信息，并充分融合它们进行分类。我们提出了一种多通道模型AM-GCN，它能够在融合拓扑和节点特征信息时学习合适的重要性权重。广泛的实验很好地证明了在真实世界数据集上，与最先进的模型相比，性能更优越。

---

后篇：
【AM-GCN】代码解读之初了解（一）
【AM-GCN】代码解读之主程序（二）
【AM-GCN】代码解读之utilis(三）
【AM-GCN】代码解读之model(四）

---

1. GCN及其变体
   GCN：$H^{(l+1)}=\sigma ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)}$ ↩︎

2. 消息传递
   $h_v^{\prime }=\phi (v)=f(h_v,g(h_u|u\in N_v))$
   其中$h_v^{\prime }$是当前节点v在当前层的输出特征，$h_v$是输入特征。$\phi (\cdot )$是表达对某个节点进行消息传递的动作。$N_v$是节点$v$的邻居集。$h_u|u\in N_v$代表遍历节点V的邻居，相当于邻居节点消息发送的动作。$g(\cdot )$是一个消息聚合函数，例如Sum,Avg,Max. ↩︎