小白入门线性回归：原理+代码

参考了好多大佬的博客、知乎、视频，链接列在文章末尾。

---

一、什么是回归

  与回归算法相对应的是分类算法，简而言之，回归就是预测一系列连续的值，分类就是预测一系列离散的值。

  那么如何把机器学习中的回归算法应用于日常生活呢？以下用一个简单的例子来说明：
  通过市场调查，我们得到一些房屋面积和价格的相关数据。我们想知道，如果给一个新的房屋面积 ，能否根据已知的数据来预测其对应价格是多少呢？如图：

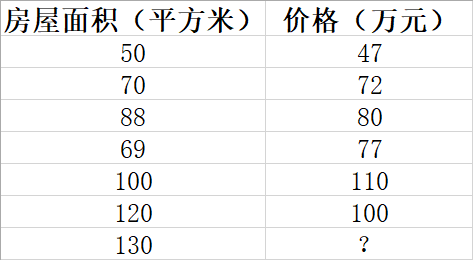
  为了解决这个问题，我们引入线性回归模型。

---

二、一元线性回归

  首先，我们画出已知数据的散点图1：

  其次，我们模拟出一条直线，让已知的数据点尽量落在直线上或直线周围。如散点图2：

  最后，我们求出这条直线模型对应的函数公式，然后代入x=130，即可求得其预测价格f(x)。

  而线性模型公式在这个例子中就是一条直线：$f(x_i)=w{x}_i+b$。其中，w为系数，b为截距。

  我们现在知道，线性回归就是要找一条直线，并且让这条直线尽可能地拟合图中的数据点。

  那么如何得到w和b从而构造这个公式呢？估计如果让1000个人来画这条线就会有1000种画法，比如说散点图3和散点图4：

  所以，我们需要一个评判标准，来评判哪条直线才是最好的。
  由此，我们引入损失函数来作为评判标准。

---

三、损失函数

  接上面的散点图3 和散点图4 两种拟合情况。对于散点图3的拟合直线$y=0.7925x+15.353$，以及散点图4的拟合直线$y=1.2452x-25$，到底哪一条直线才最“合适”呢？
  由此我们引入残差，说白了就是真实值和预测值间的差值（也可以理解为差距、距离）。即算一下实际房价和根据拟合直线的预测房价之间的差距（距离）就行了。
  当把所有实际房价和预测房价的差距（距离）算出来然后做个加和，我们就能量化预测房价和实际房价之间的残差。

  例如下图散点图5中有很多红色小竖线，每一条就是实际房价和预测房价的差距（距离）。

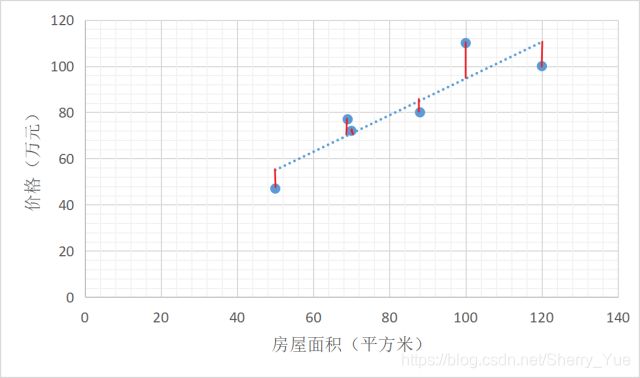
  残差公式：
  $e=y_i-f(x_i)$
  其中，f(x)是预测房价，y是真实房价。

  损失函数/残差平方和/均方误差（MSE）/欧氏距离之和：
  $J(w,b)={\sum }_{i=1}^m(y_i-f(x_i){)}^2={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$
  其中，J是损失函数，m表示样本个数，$f(x_i)$是预测值，$y_i$是真实值。

  总结，损失函数是衡量回归模型误差的函数，也就是我们要的“直线”的评价标准。
  这个函数的值越小，说明直线越能拟合我们的数据。

  好了，到这里，我们通过损失函数公式，结合散点图3参数 w=0.7925, b=15.353 ，和散点图4参数 w=1.2452, b=-25 。算得散点图3的损失函数J要小于散点图4的损失函数J。所以，可以说明，散点图3拟合的直线要比散点图4拟合的直线更“合适”。

  但是，我们不应该止步于此，我们要找的不是两者之间的更优解，而应该是所有拟合直线中的最“合适”。
  由此，我们引出最小二乘法。

---

四、最小二乘“参数估计”

  在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

  这套路，不就是已知函数$J(w,b)={\sum }_{i=1}^m(y_i-f(x_i){)}^2={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$，它有两个自变量w和b，我们要求解w和b，使得这个函数的值最小。求解w和b的过程，美名其曰线性回归模型的最小二乘“参数估计”。

  其求解过程无非就是微积分中，将J(w,b)分别对w和b求导，然后令其导数为0，便可得到w和b的最优解。此处过程略去，得到：
$$w=\frac{{\sum }_{i=1}^m{y}_i(x_i-\bar{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}$$
$$b=\frac{1}{m}\sum _{i=1}^m(y_i-w{x}_i)$$
其中，$\bar{x}=\frac{1}{m}{\sum }_{i=1}^m{x}_i$为x的均值。

  把这边解得的w和b代入预测公式$f(x_i)=w{x}_i+b$，即成功得到最合适的一元线性回归模型了。

---

五、多元线性回归

  敲醒，线性回归哪有那么简单。上面都是拿一元线性回归举的例子。可是我们生活中更常见的是多元问题。
  就比如还拿那个房价预测举例，常识可知，房价怎么可能单单看房屋面积就决定，肯定还要考虑很多其他属性，如房间数量、楼间距、离学校距离等等等等。
  所以现在依旧是m个样本做预测，但每个样本不止一个属性，而是由d个属性描述。由此，我们引入多元线性回归。

  仿照一元线性回归公式$f(x_i)=w{x}_i+b$，我们得到多元线性回归公式：
$$f(x_i)=w_1{x}_{i1}+w_2{x}_{i2}+...+w_d{x}_{id}+b$$
其中，$w_1\sim w_d$表示d个属性每个的参数（权重）；$x_{i1}\sim x_{id}$表示第i个样本，每个属性（d个）的取值，i的范围为1到m。

  我们把它改写成更高大上的向量形式：
$$f(x_i)=w^T{x}_i+b$$
其中，$w=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_d\end{array}\right]$，$w^T=\left[\begin{array}{cccc}{w}_1& w_2& \cdots & w_d\end{array}\right]$ ，$x_i=\left[\begin{array}{c}{x}_{i1}\\ x_{i2}\\ ⋮\\ x_{id}\end{array}\right]$

---

六、多元线性回归损失函数

  同理，仿照一元线性回归的损失函数$J(w,b)={\sum }_{i=1}^m(y_i-f(x_i){)}^2={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$，我们得到多元线性回归的损失函数（向量表示）：
$$J(w)=(y-Xw{)}^T(y-Xw)$$
  下面来解释这个公式：
  已知：$w=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_d\end{array}\right]$ ， $w^T=\left[\begin{array}{cccc}{w}_1& w_2& \cdots & w_d\end{array}\right]$ ，$x_i=\left[\begin{array}{c}{x}_{i1}\\ x_{i2}\\ ⋮\\ x_{id}\end{array}\right]$。
  其中$w$：把w和b吸入向量形式$w=\left[\begin{array}{c}w\\ b\end{array}\right]=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_d\\ b\end{array}\right]$。
  其中$X$：把数据集表示为一个$m\times (d+1)$大小的矩阵$X$，其中每行对应一个样本，该行前d个元素对应于样本的d个属性值，最后一个元素恒置为1。
$$X=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right]=\left[\begin{array}{cc}{x}_1^T& 1\\ x_2^T& 1\\ ⋮& ⋮\\ x_m^T& 1\end{array}\right]$$
  其中$y$：$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$。
  所以，
$$\begin{array}{rl}y-Xw& =\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]-\left[\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right]\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_d\\ b\end{array}\right]\\ & =\left[\begin{array}{c}{y}_1-w_1{x}_{11}-w_2{x}_{12}-w_d{x}_{1d}-b\\ y_2-w_1{x}_{21}-w_2{x}_{22}-w_d{x}_{2d}-b\\ ⋮\\ y_m-w_1{x}_{m1}-w_2{x}_{m2}-w_d{x}_{md}-b\end{array}\right]\\ & ={\left[\begin{array}{c}{y}_1-{\sum }_{i=1}^d{w}_i{x}_{1i}-b\\ y_2-{\sum }_{i=1}^d{w}_i{x}_{2i}-b\\ ⋮\\ y_m-{\sum }_{i=1}^d{w}_i{x}_{mi}-b\end{array}\right]}_{m\times 1}\end{array}$$
  所以$y-Xw$的平方在矩阵中即为$(y-Xw{)}^T(y-Xw)$，即得到损失函数/欧氏距离之和：$J(w)=(y-Xw{)}^T(y-Xw)$。

---

七、多元线性回归最小二乘法

  用损失函数$J(w)=(y-Xw{)}^T(y-Xw)$对$w$求导，并等于0。
  这次的解方程并没有像一元线性回归那么简单，我们需要分情况讨论：

  第一种情况：当$X^{T}X$为满秩矩阵或正定矩阵时
  得到$w$的最优解：$w=(X^{T}X{)}^{-1}{X}^{T}y$
  其中，$(X^{T}X{)}^{-1}$是$(X^{T}X)$的逆矩阵。
  令$x_i=\left[\begin{array}{c}{x}_i\\ 1\end{array}\right]$，得到最终学得的最合适的多元线性回归模型为$f(x_i)={x_i}^T(X^{T}X{)}^{-1}{X}^{T}y$。

  第二种情况：当$X^{T}X$不为满秩矩阵时
  现实任务中我们会遇到大量变量（对应大量待算属性，大量未知的w），其数目甚至超过了样本数目，导致$X$的列数多于行数，$X^{T}X$显然不满秩。
  此时可以解出多个$w$，它们都能使均方误差最小化。到底选择哪一个解作为输出呢？将由学习算法的归纳偏好决定，常见的做法是引入正则化项（说白了就是损失函数公式最后加一个$\lambda$项，不详细展开了）。

---

八、对数线性回归模型

  以上部分介绍了一元线性回归模型和多元线性回归模型。
  我们现在把模型公式来做个总结，把线性回归模型简写为：$y=w^{T}x+b$。
  其通过训练样本得出最优的w和b，从而对给定的新的样本x进行值y的预测，其实际上是在试图让模型预测值$w^{T}x+b$不断逼近真实值$y$。

  那我们是否可令模型预测值$w^{T}x+b$不断逼近真实值$y$的“衍生物”呢？比如说， 现在真实值$y$扩大为指数族中的任一分布。
  那就可将预测值的对数作为线性模型逼近的目标，这样得到的模型称为“对数线性回归”：$lny=w^{T}x+b$。它实际上是在试图让模型预测值$e^{w^{T}x+b}$不断逼近真实值$y$。
  它形式上仍是线性回归，但实质上已是在求取输入空间到输出空间的非线性函数映射。这里的对数起到了将线性回归模型的预测值与真实标记联系起来的作用。

---

九、广义线性模型

  我们可以变换上面的“对数线性回归”公式为$y=e^{w^{T}x+b}$。
  但若真实值 y 不为指数族中的分布，而变为更一般的分布呢？
  这样得到的模型，我们称为“广义线性模型”：$y=g^{-1}(w^{T}x+b)$ 。
  其中，函数$g(\cdot )$称为“联系函数”，其单调可微。
  很显然，对数线性回归是广义线性模型在$g(\cdot )=ln(\cdot )$时的特例。

---

十、pytorch实现一元线性回归

1. 网络结构

继承pytorch提供的nn.Module()类。通过把nn.Linear()绑定到类实例属性，以及实现forward()方法实现前向传播：

class LinearRegression(torch.nn.Module):
    """
    Linear Regressoin Module, the input features and output 
    features are defaults both 1
    """
    def __init__(self):
        super().__init__()
        self.linear = torch.nn.Linear(1,1)
        
    def forward(self,x):
        out = self.linear(x)
        return out

2. 优化算法选择SGD优化

self.optimizer = torch.optim.SGD(self.model.parameters(), lr=self.learning_rate)

3. 损失函数选择为MSE

self.loss_function = torch.nn.MSELoss()

4. 构建数据

构建一个类似于线性函数的数据集，即y=kx+b，并且添加一个扰动噪声：

import torch 
import matplotlib.pyplot as plt

def create_linear_data(nums_data, if_plot=False):
    """
    Create data for linear model
    Args:
        nums_data: how many data points that wanted
    Returns:
        x with shape (nums_data, 1)
    """
    x = torch.linspace(0, 1, nums_data)
    x = torch.unsqueeze(x, dim=1)
    k = 2
    y = k * x + torch.rand(x.size())

    if if_plot:
        plt.scatter(x.numpy(), y.numpy(), c='b')
        plt.show()
    data = {"x": x, "y": y}
    return data

训练测试集（100个样本）

测试数据集（20个样本）

5. 网络训练

训练网络的顺序为：读取数据—数据送入网络—得到网络输出—用输出与标签计算损失—最小化损失—更新梯度。
下列代码在训练网络过程中，同时动态绘出了每隔500个epoch的线性模型函数拟合情况：

def train(self, data, model_save_path="model.pth"):
    """
    Train the model and save the parameters
    Args:
        model_save_path: saved name of model
        data: (x, y) = data, and y = kx + b
    Returns:
        None
    """
    x = data["x"]
    y = data["y"]

    fig = plt.figure(figsize=(10, 10))
    current_fig = 0

    for epoch in range(self.epoches):
        prediction = self.model(x)
        loss = self.loss_function(prediction, y)

        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        if epoch % 500 == 0:
            print("epoch: {}, loss is: {}".format(epoch, loss.item()))
            current_fig += 1
            plt.subplot(4, 5, current_fig)
            plt.scatter(x.numpy(), y.numpy(), c='b')
            plt.plot(x.numpy(), prediction.detach().numpy(), color="r")

    plt.show()
    torch.save(self.model.state_dict(), "linear.pth")

代码最后一行torch.save()保存了模型的参数，用于测试阶段使用。
训练逐渐拟合线性回归函数的过程：

训练拟合过程

6. 模型测试

模型测试阶段需要读取训练阶段保存的参数，并重新赋值给网络：

def test(self, data, model_path="linear.pth"):
    """
    Reload and test the model, plot the prediction
    Args:
        model_path: the model's path and name
        data: (x, y) = data, and y = kx + b
    Returns:
        None
    """
    x = data["x"]
    y = data["y"]
    self.model.load_state_dict(torch.load(model_path))
    prediction = self.model(x)
    loss = self.loss_function(prediction, y)
    print("loss of test is: {}".format(loss.item()))

    plt.scatter(x.numpy(), y.numpy(), c='b', marker='x')
    plt.plot(x.numpy(), prediction.detach().numpy(), color="r")
    plt.show()

测试结果
并且得到损失值如下：

7. 完整代码

import torch
import matplotlib.pyplot as plt


def create_linear_data(nums_data, if_plot=False):
    """
    Create data for linear model
    Args:
        nums_data: how many data points that wanted
    Returns:
        x with shape (nums_data, 1)
    """
    x = torch.linspace(0, 1, nums_data)
    x = torch.unsqueeze(x, dim=1)
    k = 2
    y = k * x + torch.rand(x.size())

    if if_plot:
        plt.scatter(x.numpy(), y.numpy(), c='b')
        plt.show()
    data = {"x": x, "y": y}
    return data


class LinearRegression(torch.nn.Module):
    """
    Linear Regressoin Module, the input features and output
    features are defaults both 1
    """

    def __init__(self):
        super().__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        out = self.linear(x)
        return out


class Linear_Model():
    def __init__(self):
        """
        Initialize the Linear Model
        """
        self.learning_rate = 0.001
        self.epoches = 10000
        self.loss_function = torch.nn.MSELoss()
        self.create_model()

    def create_model(self):
        self.model = LinearRegression()
        self.optimizer = torch.optim.SGD(self.model.parameters(), lr=self.learning_rate)

    def train(self, data, model_save_path="model.pth"):
        """
        Train the model and save the parameters
        Args:
            model_save_path: saved name of model
            data: (x, y) = data, and y = kx + b
        Returns:
            None
        """
        x = data["x"]
        y = data["y"]

        fig = plt.figure(figsize=(10, 10))
        current_fig = 0

        for epoch in range(self.epoches):
            prediction = self.model(x)
            loss = self.loss_function(prediction, y)

            self.optimizer.zero_grad()
            loss.backward()
            self.optimizer.step()

            if epoch % 500 == 0:
                print("epoch: {}, loss is: {}".format(epoch, loss.item()))
                current_fig += 1
                plt.subplot(4, 5, current_fig)
                plt.scatter(x.numpy(), y.numpy(), c='b')
                plt.plot(x.numpy(), prediction.detach().numpy(), color="r")

        plt.show()
        torch.save(self.model.state_dict(), "linear.pth")

    def test(self, data, model_path="linear.pth"):
        """
        Reload and test the model, plot the prediction
        Args:
            model_path: the model's path and name
            data: (x, y) = data, and y = kx + b
        Returns:
            None
        """
        x = data["x"]
        y = data["y"]
        self.model.load_state_dict(torch.load(model_path))
        prediction = self.model(x)
        loss = self.loss_function(prediction, y)
        print("loss of test is: {}".format(loss.item()))

        plt.scatter(x.numpy(), y.numpy(), c='b', marker='x')
        plt.plot(x.numpy(), prediction.detach().numpy(), color="r")
        plt.show()


if __name__ == '__main__':
    linear = Linear_Model()
    data_train = create_linear_data(100, True)
    linear.train(data_train)
    data = create_linear_data(20, True)
    linear.test(data)

---

十一、sklearn实现多元线性回归

案例：波士顿房价预测
网上关于个这个的资料和代码实在是太多了，这边列出几个网址，这篇文章里就不详细讲了，套路都是一样的。

1. 【机器学习】线性回归sklearn实现 - AI_developer - 博客园
2. https://blog.csdn.net/qq_28827635/article/details/84481414
3. https://my.oschina.net/u/2245781/blog/1855834
4. https://github.com/TalkEveryX/Linear_Model/blob/master/boston_housing.py

---

十二、参考资料

1. https://blog.csdn.net/alw_123/article/details/82193535
2. https://blog.csdn.net/alw_123/article/details/82825785
3. 化简可得：用人话讲明白线性回归LinearRegression
4. 人人都会机器学习：线性回归模型原理及推导
5. 王伟同学：线性回归：这可能是机器学习中最简单的一个模型了
6. 线性回归（Linear Regression）
7. https://blog.csdn.net/pxhdky/article/details/82388964
8. 周志华《机器学习》
9. 机器学习入坑者：线性回归模型与pytorch实现
10. https://zhuanlan.zhihu.com/p/59401172