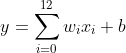波士顿房价预测(终版讲解)
代码段分四个部分:库的引入、加载数据(函数)、配置网络结构(类)、运行部分(获取数据,创建网络,启动训练,作图)
我的是基础版,库只用到了numpy和matplotlib的pyplto两个。
加载数据需要进行将数据作为数组输入,重整成14*N的二维数组,分训练集和测试集并归一化
重点在配置网络结构部分。搭建神经网络:搭建神经网络就像是用积木搭宝塔。在飞桨中,网络层(layer)是积木,而神精网络是要搭建的宝塔 这里通过创建python类的方式完成模型网络的定义,即定义__init__函数和forward函数等。
最后通过调用函数完成模型的训练并作出loss的图
第一部分:库的引入
#加载相关库
import numpy as np
import matplotlib.pyplot as plt这一部分没什么好说的。paddle版的库引入库可能会比较复杂,这里基础班只用到这两个库。
第二部分:加载数据
#数据预处理
def load_data():
datafile = './data/data108228/housing.data'
data = np.fromfile(datafile,sep=' ') #分隔符:如果一个文件是文本文件,默认空格分隔
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)
data = data.reshape(data.shape[0]//feature_num,feature_num)
ratio = 0.8
offset=int(data.shape[0]*ratio)
training_data = data[:offset]
maximums, minimums, avge = training_data.max(axis=0), training_data.min(axis=0), training_data.sum(axis=0) / training_data.shape[0]
#记录数据的归一化参数,在预测时对数据归一化
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avge
#有的案例加了有的没加,不明白为什么要加,先加上了
for i in range(feature_num):
data[:, i] = (data[:, i]-avge[i]) / (maximums[i]-minimums[i])
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_dataload_data函数返回训练集和测试集两个数组
首先加载文件,这里的分隔符是空格,所以写sep=' '
然后将十三个预测参数和lable的名字给feature_names,用feature_num记录参数的个数,下面要用到feature_num这个变量。
之后重整数据,读入的是一维的数据,需要将它转换为二维的14*N的二维数据
接下来是分组和归一化。由于所有数据都要用训练集的范围来进行归一化操作,先找到训练集,计算出它的最值和均值(其中的axis=0是对第零维,也就是行进行操作)去对所有数据进行归一化,归一化完成后分成两组输出。
第三步:配置网络结构
#数据预处理
def load_data():
datafile = './data/data108228/housing.data'
data = np.fromfile(datafile,sep=' ') #分隔符:如果一个文件是文本文件,默认空格分隔
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
feature_num = len(feature_names)
data = data.reshape(data.shape[0]//feature_num,feature_num)
ratio = 0.8
offset=int(data.shape[0]*ratio)
training_data = data[:offset]
maximums, minimums, avge = training_data.max(axis=0), training_data.min(axis=0), training_data.sum(axis=0) / training_data.shape[0]
#记录数据的归一化参数,在预测时对数据归一化
global max_values
global min_values
global avg_values
max_values = maximums
min_values = minimums
avg_values = avge
#有的案例加了有的没加,不明白为什么要加,先加上了
for i in range(feature_num):
data[:, i] = (data[:, i]-avge[i]) / (maximums[i]-minimums[i])
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
In [8]
#配置网络结构
class Network(object):
def __init__(self, num_of_weights):
np.random.seed(0) # 随机产生w的初始值,为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z-y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta=0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses=[]
for epoch_id in range(num_epochs):
np.random.shuffle(training_data)
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:4f}'.format(epoch_id, iter_id, loss))
return losses这一步是核心拆开来解析:
class Network(object):
def __init__(self, num_of_weights):
np.random.seed(0) # 随机产生w的初始值,为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.创建一个类:Network,这种数据类型中包含两部分,w数组和b,因为自变量有13个,所以它们的系数需要一个数组来存,b就初始化为0就可以
def forward(self, x):
z = np.dot(x, self.w) + self.b
return zforward函数 forward函数是框架指定实现向前计算逻辑的函数,返回预测结果。用当前w和x点乘,返回预测结果y(bar)
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost计算损失函数,返回损失值,是个平均数,注意是一个数。
def gradient(self, x, y):
z = self.forward(x)
gradient_w = (z-y)*x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = (z-y)
gradient_b = np.mean(gradient_b)
return gradient_w, gradient_b计算梯度函数,先算出用当前w预测的结果,然后用结果算出梯度并求均值。公式就是求偏导。gradient_w需要按行平均,平均后是[w0,w1,,,,,,w12],shape=(13,),但w是(13,1)所以需要给gradient_w添加新的一维(虚的)。
返回两个梯度,w的是数组,b的是一个数
def update(self, gradient_w, gradient_b, eta=0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b更新函数。完成更新操作,原系数 - 学习率和梯度的乘积
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses=[]
for epoch_id in range(num_epochs):
np.random.shuffle(training_data)
mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches): #在字典上是枚举的意思
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print('Epoch {:3d} / iter {:3d}, loss = {:4f}'.format(epoch_id, iter_id, loss))
return losses两层循环:
第一层进行num_epochs(迭代周期)次。每次先打乱数据,将数据分组(,每组长度为batch_size,之后嵌套下一层循环
第二层遍历mini_batchs。先将它分成参数和label,计算预测值,损失函数和梯度。更新w
输出当前的轮次,索引和损失函数。并记录每一个loss到losses里,方便作图。
enumerate用处:遍历索引和元素。
list1 = ["this", "is", "a", "test"]
for index, item in enumerate(list1):
print index, item
>>>
0 this
1 is
2 a
3 test第四步:启动训练
training_data, test_data = load_data()
net = Network(13)
losses = net.train(training_data, num_epochs=50, batch_size=100, eta=0.1)
plot_x = np.arange(len(losses)) #返回有起点和终点的固定步长的排列
plot_y = np.array(losses)
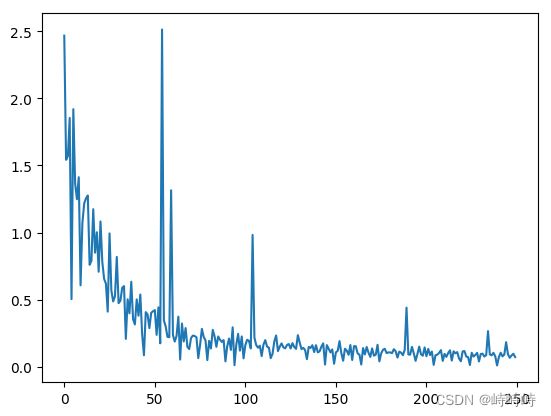
plt.plot(plot_x, plot_y)
plt.show()很简单,直接看结果:
Epoch 0 / iter 0, loss = 2.467436
Epoch 0 / iter 1, loss = 1.541610
Epoch 0 / iter 2, loss = 1.569710
Epoch 0 / iter 3, loss = 1.853896
Epoch 0 / iter 4, loss = 0.503186
Epoch 1 / iter 0, loss = 1.919441
.
.
.
Epoch 49 / iter 0, loss = 0.093340
Epoch 49 / iter 1, loss = 0.066011
Epoch 49 / iter 2, loss = 0.083206
Epoch 49 / iter 3, loss = 0.096158
Epoch 49 / iter 4, loss = 0.071400
这样房价预测模型就训练完了
保存模型用到 np.save('w.npy', net.w)
np.save('b.npy', net.b)
模型的测试在下一个版本记录