西北工业大学2021数模校赛B题 - 波士顿房价的预测

西北工业大学2021数模校赛B题 - 波士顿房价的预测

一.文章声明：

本篇文章是笔者自己结合网上的资料进行学习与建模的过程与心得，本人是python大数据小白，所以在拿到类似数据挖掘的题目时就向着数据挖掘的方向进行前进，5.1-5.3三天校赛数模主编程，第一次数模如有不正确不合适的地方，敬请指正，谢谢！！

二.题目简述：

由于本次B题的3，4问中开放性较高，所以本篇文章仅针对前两个问题进行解析与解答

三.使用python机器学习对于问题进行分析：

首先打开pycharm使用python进行环境变量的配置：

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
import seaborn as sns
import os
from scipy.stats import f as F_TEST

3.1 数据基本样貌解析：

问题一总述分析：
首先我们将所给附件转换为csv格式文件，使用Python的Pandas库将数据导入，用matplotlib和seaborn库绘制前13个变量与第14个变量户主拥有住房价值的中位数（以下简称房价）的散点图，以及变量间的热力相关图，分析出自变量与房价的线性相关关系，以及每一个自变量对房价的影响情况
加载数据集：

os.chdir(r'C:\Users\86135\Desktop\数模校赛B题')
f=open("boston.csv",encoding="utf-8")
df=pd.read_csv(f)

使用dataframe进行数据统计数据基本样貌：

data_pd=pd.DataFrame(data=df,columns=df.columns)
data_des=data_pd.describe()
data_des.plot()
plt.title("Description of data")
plt.legend(loc="best")
plt.savefig("数据基本样貌折线图.png")
plt.show()

对于数据基本面貌的折线图：

作出13个属性对于房价的影响的散点图：

plt.rcParams['font.sans-serif']=['SimHei']              #解决中文无法显示的问题
plt.rcParams['axes.unicode_minus']=False                #用来正常显示负号
titles=['CRIM','LRA','NCS','CR','NOX','ARN','HOB','WD5','RH','TAX','SFR','POAA','LSSP'] #设置标题
plt.figure(figsize=(12,9))                              #配置画布大小
for i in range(13):
    plt.subplot(4,4,i+1)
    plt.scatter(data_pd[titles[i]],data_pd['MV'],marker=".",color='g')
    plt.xlabel(titles[i])
    plt.title(str(i+1)+'.'+titles[i]+'-MV')
plt.tight_layout()
plt.savefig("13个属性的散点图")                            #依次做出13个图并且可视化
plt.show()

13个属性的散点图：

计算相关系数，选出相关系数>0.5的因素作为主要影响因素进行绘图：

print(data_pd.corr()['MV'])
corr = data_pd.corr()
corr = corr['MV']
corr[abs(corr)>0.5].sort_values().plot.bar(color=['lightblue','lightgreen','lightpink','orange'])
plt.title("Show the factors with correlation coefficient > 0.5")
plt.savefig("pearson_sorted_0.5.png")
plt.show()

主要因素：

对于上面的三个主属性进行散点绘图与放大分析：

#展示LSSP和MV之间的关系：
plt.scatter(data_pd['LSSP'],data_pd['MV'],c="lightblue")
plt.title("LSSP - MV")
plt.savefig("LSSP_MV散点图.png")
plt.show()

#展示SFR和MV之间的关系
plt.scatter(data_pd['SFR'],data_pd['MV'],c="lightgreen")
plt.title("SFR - MV")
plt.savefig("SFR_MV散点图.png")
plt.show()

#展示ARN和MV之间的关系
plt.scatter(data_pd['ARN'],data_pd['MV'],c="pink")
plt.title("ARN - MV")
plt.savefig("ARN_MV散点图.png")
plt.show()

三个主属性的相关散点图：



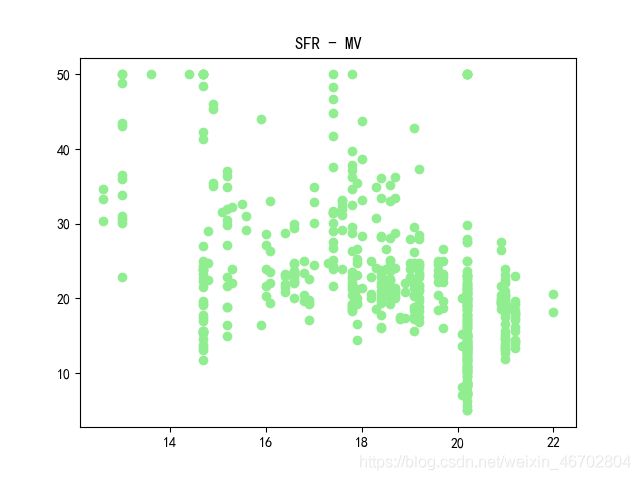
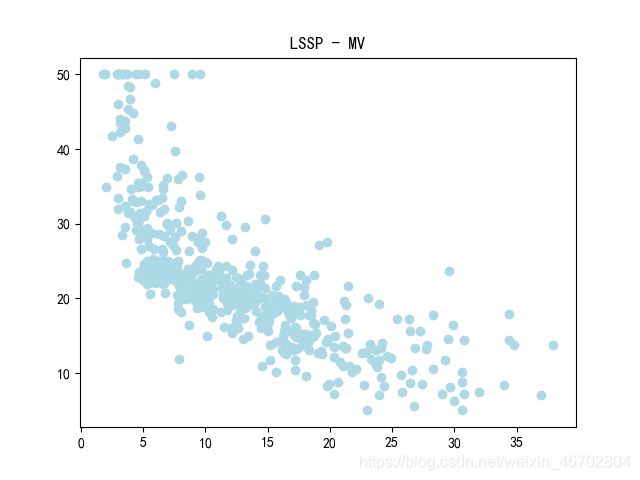
由散点图可以看出，部分变量与房价有比较明显的相关关系，同时从热力相关图的最后一行（13个自变量和房价的相关系数）可以看出，绝大多数的变量与房价的相关系数都超过了0.3，其中有3个超过了0.5，分别为ARN、SFR、LSSP，有着较为明显的相关关系。

3.2 数据相关性简介：

使用热力图进行属性之间的相关性解析：

_, ax = plt.subplots(figsize=(12, 10)) #分辨率1200×1000
ax.set_title("Pearson Heatmap")
corr = df.corr(method='pearson') # 使用皮尔逊系数计算列与列的相关性
sns.heatmap(corr,square=True,cmap="rainbow",cbar_kws={'shrink': .9},ax=ax,annot=True,annot_kws={'fontsize': 12})
plt.savefig("pearson_heatmap.png")
plt.show()

热力相关图：

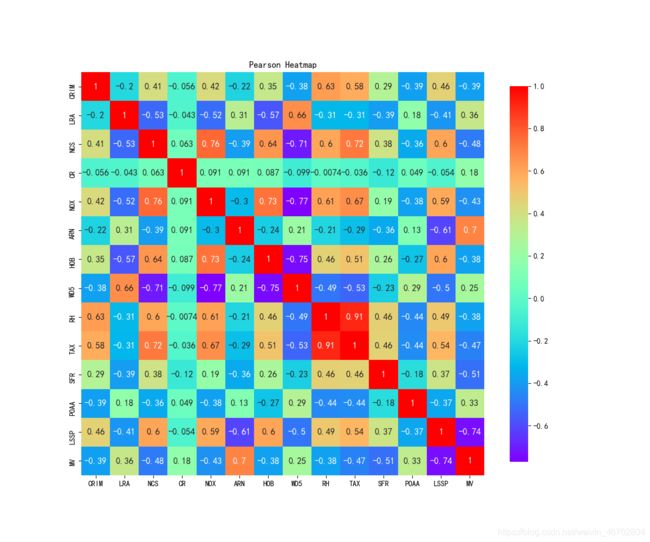
根据13个变量与房价的相关系数（以及热力图中的观测）来说明单个变量如何影响房价并做出一定的解释：
CRIM： 与房价的相关系数为-0.39，为负值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，人均犯罪率高的地区，房价相对低，并且相关程度中等。实际上，人均犯罪率高的地区治安差，人群受教育程度低，黑势力较为集中，房价就较低。
LRA： 与房价的相关系数为0.36，为正值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，大块占地住宅区比例高的地区，房价相对高，并且相关程度中等。实际上LRA，反映的是与市中心的接近程度，显然越接近市中心的地区LRA越高，房价也越高，呈正相关，符合实际情况。
NCS： 与房价的相关系数为-0.48，为负值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，非零售商业占地比例高的地区，房价相对低，相关程度中等。根据资料显示，波士顿的批发厂主要分布在离市中心较远的地区，所以该变量同样能反映距离市中心的距离，比例越大，离市中心越远，房价越低。
CR： 与房价的相关系数为0.18，为正值且绝对值在0.3以下，说明在其它因素相同的情况下，靠近河流的地区，其房价相对高一点，相关程度较弱。实际上，靠近河流的地区，其自然环境相对较好，交通运输相对便利，但可能距离市中心较远，故综合起来看，房价受它的影响不大。更为关键的因素是，CR的取值只有0，1两种，故与其它变量的相关性不能明确的表现。
NOX： 与房价的相关系数为-0.43，为负值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，氮氧化物浓度高的地区，房价相对低，相关程度中等。实际上，氮氧化物浓度高的地区主要在大型工厂附近，自然环境相对差，且距离市中心较远，故房价相对低。
ARN： 与房价的相关系数为0.7，为正值且绝对值大于0.5，说明在其它因素相同的情况下，每户平均房间数高的地区，房价相对高，相关程度较强。实际上，房价最直接的影响因素就是房屋面积，每户平均房间数高的地区，其房屋面积大，甚至可能为别墅区，房价固然高并且影响程度较大。
HOB： 与房价的相关系数为-0.38，为负值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，1940年前建造的户主所有房比例大的地区，房价相对低，相关程度中等。实际上，HOB能反映该地区城市化的程度，HOB越大，说明该地区老旧房屋占比大，城市化程度低，房价自然相对较低。
WD5： 与房价的相关系数为0.25，为正值且绝对值在0.3以下，说明在其它因素相同的情况下，与五个波士顿劳动力聚集区的加权距离大的地区，房价相对高，相关程度较弱。理论上，WD5越大，说明该地区距离中心区相对远，房价应该相对低，但实际上，WD5不能准确的说明该地区是否在市区或者郊区，并且可能考虑到郊区别墅高房价、环境优的影响，使得WD5与房价表现了较弱的正相关性，与理论分析略有不同。
RH： 与房价的相关系数为-0.38，为负值并且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，与辐射式公路的接近指数大的地区，房价相对低。相关程度中等。实际上，RH反映了该地区的交通情况，RH越小，说明附近交通便利，房价相对高。
TAX： 与房价的相关系数为-0.47，为负值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，每一万美元的全值财产税大的地区，房价相对较低。相关程度中等。实际上，TAX越大，说明财产税越大，更少人愿意去买，故而房价低。
SFR： 与房价的相关系数为-0.51，为负值且绝对值在0.5以上，说明在其它因素相同的情况下，学生与教师的比例大的区，房价相对低，相关程度较强。实际上，SFR反映了该地区的教育程度和学校的密集程度，SFR越小，说明教师相对学生多，教育程度高，并且附近学校较多，也可能为学区房，故房价高，呈现负相关。
POAA： 与房价的相关系数为0.33，为正值且绝对值在0.3~0.5之间，说明在其它因素相同的情况下，POAA大的地区，房价相对较高，相关程度中等。实际上，POAA反映了非洲裔美国人的比例，POAA高的地区，非洲裔美国人的比例小，由于美国种族因素的影响，黑人比例大的地区，往往人均社会地位相对较低，房价也低，故POAA高的地区黑人比例小，房价相对高。
LSSP： 与房价的相关系数为-0.74，为负值且绝对值在0.5以上，说明在其它因素相同的情况下，低社会地位人口的比例高的地区，房价相对低，相关程度较强。实际上LSSP越高，说明该地区处于较低层次的社会，生活质量相对低，房价低。

3.3 机器学习与建模部分（使用原数据）：

依次使用四种回归模型分别进行建模以及评价：

data_pd = pd.DataFrame(data=df,columns=df.columns)
data_pd = data_pd[['CRIM','LRA','NCS','CR','NOX','ARN','HOB','WD5','RH','TAX','SFR','POAA','LSSP','MV']]
y = np.array(data_pd['MV'])
data_pd=data_pd.drop(['MV'],axis=1)
X = np.array(data_pd)

# 分割训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=14)

print("--------------------LR-------------------------")
lr=LinearRegression()
lr.fit(X_train,y_train)
y_lr_pred=lr.predict(X_test)
error_lr=mean_squared_error(y_test,y_lr_pred)
print('斜率：',lr.coef_)
print('截距：',lr.intercept_)
print('均方误差：',error_lr)
#计算SST和R^2
ssr_lr=np.sum((y_lr_pred - np.mean(y_test)) ** 2)
R2_lr = 1-error_lr/ssr_lr
print('R方',R2_lr)
#F检验
up = ssr_lr/14
down = error_lr / (506-14-1)
F_lr = up/down
print("实际F值：",F_lr)
F_Theroy_lr=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_lr)

print("------------------------SGD--------------------")
sgd=SGDRegressor()
sgd.fit(X_train,y_train)
y_sgd_pred=sgd.predict(X_test)
error_sgd=mean_squared_error(y_test,y_sgd_pred)
print('斜率：',sgd.coef_)
print('截距：',sgd.intercept_)
print('均方误差：',error_sgd)
#计算SST和R^2
ssr_sgd =np.sum((y_sgd_pred - np.mean(y_test)) ** 2)
R2_sgd = 1-error_sgd/ssr_sgd
print(R2_sgd)
#F检验
up = ssr_sgd/14
down = error_sgd / (506-14-1)
F_sgd = up/down
print("实际F值：",F_sgd)
F_Theroy_sgd=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_sgd)

print("--------------------------LASSO--------------------------")
# 找到Lasso的alapha值
model = LassoCV(cv=20).fit(X, y)
# 进行Lasso回归
lasso = Lasso(max_iter=10000, alpha=model.alpha_)
lasso.fit(X_train, y_train)
y_pred_lasso =lasso.predict(X_test)
# 输出Lasso系数
print('斜率：',lasso.coef_)
print('截距：',lasso.intercept_)
print('lasso回归均方误差：',mean_squared_error(y_test,y_pred_lasso))
SSE = mean_squared_error(y_test,y_pred_lasso)
SSR = np.sum((y_pred_lasso - np.mean(y_test)) ** 2)
R2 = 1- SSE/SSR
print(R2)
#F检验
up = SSR /14
down = SSE / (506-14-1)
F_la = up/down
print("实际F值：",F_la)
F_Theroy_la=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_la)

print("-----------------------------Reidge-----------------------")
rd=Ridge()
rd.fit(X_train,y_train)
print(rd.coef_)
print(rd.intercept_)
y_rd_pred=rd.predict(X_test)
print('岭回归下均方误差：',mean_squared_error(y_test,y_rd_pred))
sse = mean_squared_error(y_test,y_rd_pred)
#计算SST和R^2：
ssr_rd = np.sum((y_rd_pred - np.mean(y_test)) ** 2)
R2_rd = 1 - sse / ssr_rd
print(R2_rd)
#F检验：
up = ssr_rd/14
down = sse / (506-14-1)
F_rd = up/down
print("实际F值：",F_rd)
F_Theroy_rd=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_rd)

运行结果展示：

正则化线性回归：
MV = - 9.21274736 * 10^-2 CRIM + 5.02784306 * 10^-2 LRA + 2.15284959 * 10^-2 NCS + 3.02469962 CR - 1.83410939 * 10^1 NOX + 3.91521885 ARN + 9.58916188 * 10^-3 HOB - 1.47452651 WD5 + 2.87337465 * 10^-1 RH - 1.20880049 * 10^-2 TAX - 9.91327765 * 10^-1 SFR + 6.01417187 * 10 ^-3 POAA - 5.63066192 * 10^-1 LSSP + 37.82941413023578

均方误差： 24.523741433124314
R方： 0.9957443759609029
实际F值： 8241.195239340266
理论F值： 2.118070479011805
---------------------------------------------------------------------------------------------------------------------------------
随机梯度下降回归：
MV = 3.37107738 * 10^10 CRIM + 5.21684013 * 10^11 LRA + 7.58522088 * 10^10 NCS + 1.47131403 * 10^10 CR + 6.73006346 * 10^9 NOX + 1.56414904 * 10^11 ARN + 1.00842835 * 10^11 HOB - 2.91362739 * 10^11 WD5 - 5.62180874 * 10^11 RH + 3.70666065 * 10^11 TAX - 4.25357407 * 10^11 SFR + 7.78190929 * 10^10 POAA - 3.76696379 * 10^11 LSSP - 9.52593132 *10^9

均方误差： 3.5223887252021308 * 10^28
R方： 0.9901960784313725
实际F值： 3577.285714285674
理论F值： 2.118070479011805
---------------------------------------------------------------------------------------------------------------------------------
Lasso回归：
MV = - 0.05735935 CRIM + 0.05190773 LRA - 0.0 NCS + 0.0 CR - 0.0 NOX + 2.02345913 ARN + 0.02554581 HOB - 0.69626584 WD5 + 0.25975989 RH - 0.01531205 TAX - 0.77482949 SFR + 0.00573684 POAA - 0.75441197 LSSP + 35.951395510062476
 
均方误差： 26.10064040505063
R方： 0.9952365271230845
实际F值： 7362.575473325399
理论F值： 2.118070479011805
---------------------------------------------------------------------------------------------------------------------------------
岭回归：
MV = - 8.71811362 * 10^-2 CRIM + 5.17323108 * 10^-2 LRA - 7.87028765 * 10^-3 NCS + 2.86136009 CR - 1.01757489 * 10 NOX + 3.96736900 ARN + 3.11907031 * 10^-3 HOB - 1.33551369 WD5 + 2.72485657 * 10^-1 RH - 1.30064740 * 10^-2 TAX - 8.97488401 * 10^-1 SFR + 6.41338767 * 10^-3 POAA - 5.75516375 * 10^-1 LSSP + 31.997674854058808

均方误差： 24.570308877217364
R方： 0.9956876090864352
实际F值： 8132.710896201309
理论F值： 2.118070479011805

3.4 机器学习与建模部分（数据标准化）：

在机器学习时将原始数据进行标准化之后再依次构建四种回归模型并进行检验：

# 制作训练集和测试集的数据
data_pd = data_pd[['CRIM','LRA','NCS','CR','NOX','ARN','HOB','WD5','RH','TAX','SFR','POAA','LSSP','MV']]
Y = np.array(data_pd['MV'])
data_pd=data_pd.drop(['MV'],axis=1)
X = np.array(data_pd)
X_train,X_test,y_train,y_test=train_test_split(X,Y,random_state=33,test_size=0.2)

#标准化
std=StandardScaler()
x_train=std.fit_transform(X_train)
x_test=std.transform(X_test)
y_train=std.fit_transform(y_train.reshape(-1,1))  #y需要转化为2维
y_test=std.transform(y_test.reshape(-1,1))

print("-----正则化LinearRegression-----")
lr=LinearRegression()
lr.fit(x_train,y_train)
y_lr_pred=std.inverse_transform(lr.predict(x_test))
error_lr=mean_squared_error(std.inverse_transform(y_test),y_lr_pred)
print('斜率：',lr.coef_)
print('截距：',lr.intercept_)
print('均方误差：',error_lr)
#计算SST和R^2
ssr_lr=np.sum((y_lr_pred - np.mean(y_test)) ** 2)
R2_lr = 1-error_lr/ssr_lr
print(R2_lr)
#F检验
up = ssr_lr/14
down = error_lr / (506-14-1)
F_lr = up/down
print("实际F值：",F_lr)
F_Theroy_lr=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_lr)

print("-----随机梯度下降法SGDRegressor-----")
sgd=SGDRegressor()
sgd.fit(x_train,y_train)
y_sgd_pred=std.inverse_transform(sgd.predict(x_test))
error_sgd=mean_squared_error(std.inverse_transform(y_test),y_sgd_pred)
print('斜率：',sgd.coef_)
print('截距：',sgd.intercept_)
print('均方误差：',error_sgd)
#计算SST和R^2
ssr_sgd =np.sum((y_sgd_pred - np.mean(y_test)) ** 2)
R2_sgd = 1-error_sgd/ssr_sgd
print(R2_sgd)
#F检验
up = ssr_sgd/14
down = error_sgd / (506-14-1)
F_sgd = up/down
print("实际F值：",F_sgd)
F_Theroy_sgd=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_sgd)

print("----------------Lasso回归----------------------")
lasso = Lasso()
lasso.fit(X_train, y_train)
y_pred_lasso =lasso.predict(X_test)
# 输出Lasso系数
print('斜率：',lasso.coef_)
print('截距：',lasso.intercept_)
print('lasso回归均方误差：',mean_squared_error(y_test,y_pred_lasso))
sse_la = mean_squared_error(y_test,y_pred_lasso)
ssr_la = np.sum((y_pred_lasso - np.mean(y_test)) ** 2)
R2 = 1- sse_la/ssr_la
print(R2)
#F检验
up = ssr_la/14
down = sse_la / (506-14-1)
F_la = up/down
print("实际F值：",F_la)
F_Theroy_la=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_la)


print("-----岭回归Ridge-----")
rd=Ridge(alpha=1.0)
rd.fit(x_train,y_train)
print(rd.coef_)
print(rd.intercept_)
y_rd_pred=std.inverse_transform(rd.predict(x_test))
print('岭回归下均方误差：',mean_squared_error(std.inverse_transform(y_test),y_rd_pred))
sse = mean_squared_error(std.inverse_transform(y_test),y_rd_pred)
#计算SST和R^2：
ssr_rd = np.sum((y_rd_pred - np.mean(y_test)) ** 2)
R2_rd = 1 - sse / ssr_rd
print(R2_rd)
#F检验：
up = ssr_rd/14
down = sse / (506-14-1)
F_rd = up/down
print("实际F值：",F_rd)
F_Theroy_rd=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_rd)

运行结果展示：

正则化线性回归：
MV = - 0.10652353 CRIM + 0.1248883 LRA + 0.02144814 NCS + 0.08447264 CR - 0.1851724 NOX +  0.3015255 ARN - 0.00436415 HOB - 0.33801186 WD5 + 0.28858221 RH - 0.23677719 TAX - 0.19424453 SFR + 0.07916941 POAA - 0.43398872 LSSP + 4.18819804 * 10 ^ -15

均方误差： 22.042579216213284
R方： 0.9995876421553258
实际F值： 85050.95519435528
理论F值： 2.118070479011805
---------------------------------------------------------------------------------------------------------------------------------
随机梯度下降回归：
MV = - 0.09017088 CRIM + 0.09381253 LRA - 0.029617 NCS + 0.09407728 CR - 0.13883074 NOX +  0.32370686 ARN - 0.01647585 HOB - 0.29189313 WD5 + 0.16190143 RH - 0.1052844 TAX - 0.1859067 SFR + 0.08232581 POAA - 0.42638702 LSSP + 1.36533229 * 10 ^ -5

均方误差： 22.293789831144753
R方： 0.9995866669969736
实际F值： 84850.29822113655
理论F值： 2.118070479011805
---------------------------------------------------------------------------------------------------------------------------------
Lasso回归：
MV = - 0.0 CRIM + 0.00218933 LRA - 0.0 NCS + 0.0 CR + 0.0 NOX + 0.0 ARN + 0.00084594 HOB - 0.0 WD5 + 0.0 RH - 0.00092818 TAX - 0.0 SFR + 0.00082548 POAA - 0.06964242 LSSP + 0.8517611

均方误差： 0.337201147275985
R方： 0.9934775184507464
实际F值： 5377.006942310473
理论F值： 2.118070479011805
---------------------------------------------------------------------------------------------------------------------------------
岭回归：
MV = - 0.10546956 CRIM + 0.12265543 LRA + 0.01810155 NCS + 0.08491327 CR - 0.18178902 NOX + 0.30268784 ARN - 0.00504133 HOB - 0.33433398 WD5 + 0.27964259 RH - 0.2279551 TAX - 0.19351241 SFR + 0.07916974 POAA - 0.43224374 LSSP + 4.19852261 * 10^-15

均方误差： 21.982909442895057
R方： 0.9995888250657292
实际F值： 85295.63854282866
理论F值： 2.118070479011805

3.5 模型评价以及数据分析：

数据分析：

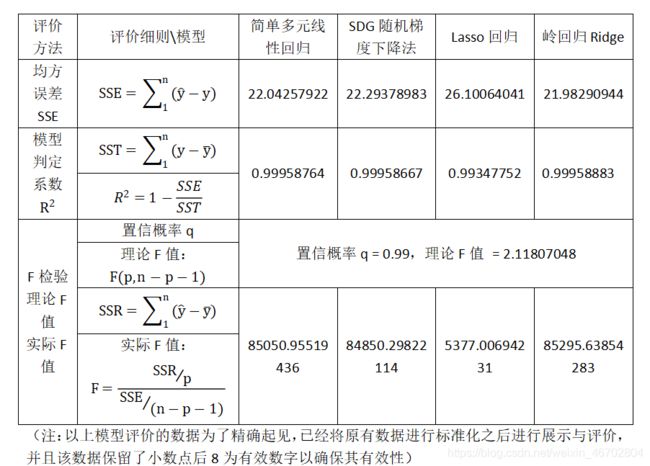
• （1）均方误差SSE： 均方误差表示的是真实值和估计值差的平方和，对于一个回归数学模型的评价中均方误差的值应越小越好，通过比较上面的数据我们可知在均方误差这方面评估模型的优劣性上：岭回归Ridge模型 > 简单多元线性回归模型 > SDG随机梯度下降法模型 > Lasso回归模型 （此处 > 表示优于，下同），说明岭回归Ridge模型总体山真实值跟模型构建出的估计值相差是相对较小的，因此在均方误差上岭回归Ridge模型同样是优于其他三个模型的，这就说明岭回归Ridge模型的模型拟合的精确程度是优于其他三个模型
• （2）模型判定系数： 模型判定系数表示的是模型拟合的好坏，且其取值范围为[ 0 , 1 ]，因此对于判定系数的评价标准有 > 0.8 即可认为拟合程度好，模型可以用于拟合，通过上面的数据我们可知，本次解决问题使用的四个模型的判定系数均 > 0.99 因此说明这四个模型的拟合均可以用于问题的解决，但精确地看其优劣程度，我们不难发现： 岭回归Ridge模型 > 简单多元线性回归模型 > SDG随机梯度下降法模型 > Lasso回归模型 ，因此在判定系数上岭回归Ridge模型同样也是优于其他三个模型的，这就说明岭回归Ridge模型的模型拟合的精确程度是优于其他三个模型
• （3）F检验： F检验分为两部分：理论F值和实际F值：对于理论F值中置信系数q的选择范围是在[ 0 , 1 ]之间，本次我们规范了置信系数为0.99，因此原数据给定的情况下，理论F值是相同的，均为2.11807048 ；对于实际F值，每一个模型是不同的，对于一个模型来说，实际F值 - 理论F值的差值越大，则说明模型的拟合程度越好，理论上差值在100以上就可以说明该模型的精确度较高，因此通过上面的数据，我们可知每个模型的拟合精确程度都较高，但是精确来看是：岭回归Ridge模型 > 简单多元线性回归模型 > SDG随机梯度下降法模型 > Lasso回归模型，因此在F检验上岭回归Ridge模型同样也是优于其他三个模型的，这就说明岭回归Ridge模型的模型拟合的精确程度是优于其他三个模型
• （4）总结（1）（2）（3），通过上面的三条分析，我们不难发现岭回归Ridge模型在各个方面都是优于其他三个模型的，这就说明岭回归Ridge模型的模型拟合的精确程度在总体上确实是优于其他三个模型的，因此在本次数学建模解决问题中，我们最终选择使用岭回归Ridge回归模型作为解决问题的最终模型

3.6 仅对于岭回归中k值较大的4个属性进行单独回归建模：

由3.4中的运行结果可以看到对于岭回归中k值较大的四个属性分别是：‘ARN’,‘WD5’,‘SFR’,'LSSP’这四个，因此将这四个属性单独拎出来进行回归建模：

# 导包
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
import os
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from scipy.stats import f as F_TEST

os.chdir(r'C:\Users\86135\Desktop\数模校赛B题')
f=open("boston.csv",encoding="utf-8")
df=pd.read_csv(f)

#用dataframe进行数据统计
data_pd=pd.DataFrame(data=df,columns=df.columns)
data_pd = data_pd[['ARN','WD5','SFR','LSSP','MV']]
Y = np.array(data_pd['MV'])
data_pd=data_pd.drop(['MV'],axis=1)
X = np.array(data_pd)
X_train,X_test,y_train,y_test=train_test_split(X,Y,random_state=33,test_size=0.2)
#标准化
std=StandardScaler()
x_train=std.fit_transform(X_train)
x_test=std.transform(X_test)
y_train=std.fit_transform(y_train.reshape(-1,1))  #y需要转化为2维
y_test=std.transform(y_test.reshape(-1,1))

rd=Ridge(alpha=1.0)
rd.fit(x_train,y_train)
print(rd.coef_)
print(rd.intercept_)
y_rd_pred=std.inverse_transform(rd.predict(x_test))
print('岭回归下均方误差：',mean_squared_error(std.inverse_transform(y_test),y_rd_pred))
sse = mean_squared_error(std.inverse_transform(y_test),y_rd_pred)
#计算SST和R^2
sst = np.sum((y_rd_pred - np.mean(y_test)) ** 2)
R2 = 1 - sse / sst
print(R2)
#F检验：
up = sst / 14
down = sse / (506-14-1)
F_rd = up/down
print("实际F值：",F_rd)
F_Theroy_rd=F_TEST.ppf(q=0.99,dfn=14,dfd=506-14-1)
print("理论F值：",F_Theroy_rd)

运行结果展示：

4个主要特征岭回归：
MV = 0.33252121 ARN - 0.14154463 WD5 - 0.20936303 SFR - 0.53067059 LSSP + 5.75531201 * 10^-15

均方误差： 26.522384226498634
R方： 0.9995205616473111
实际F值： 73151.07015267797
理论F值： 2.118070479011805