NNDL 作业4：第四章课后题

文章目章

前言

一、习题4-2  试设计一个前馈神经网络来解决 XOR 问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用 ReLU 作为激活函数．

4.2.1  网络的构建

 4.2.2   参数的设置

 4.2.3  训练模型

4.2.4   打印训练结果

4.2.5  可视化

4.2.6 与感知机的比较 

二、习题4-3 试举例说明“死亡ReLU问题”，并提出解决方法.

好了，废话说完了，我们来看一下，代码实例这个是用ReLU来实现的。

使用Leaky ReLU进行模型训练

三、习题4-7 为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化? 

四、习题 4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 w= 0, = 0？

五、习题4-9 梯度消失问题是否可以通过增加学习率来缓解？

总结

---

前言

       这次我还是写的很细，有好多东西查了好多资料，有的我给出链接，真的学到很多，而且这次是一口气写完的，一口气写的真的感觉很连贯，很通畅。

       这次作业是写了一下午到这会了，晚饭都没吃，饭要凉了，但是真的很爽，写完去吃了(哈哈哈)，并且疫情终于要过去了，现在中风险了，有大块的时间来写这个了,河大加油。  

       最后，我在下边，提出了我发现的问题，希望老师和各位大佬帮忙解答一下，去吃饭了(哈哈哈)

---

 

一、习题4-2  试设计一个前馈神经网络来解决 XOR 问题，要求该前馈神经网络具有两个隐藏神经元和一个输出神经元，并使用 ReLU 作为激活函数．

       首先，先说一下，大家都知道咱们用神经网络来解决异或问题的原因是，感知机并不能很好的解决。至于这个的证明，我会在下边放一下(因为之前考试的时候考过，当时想了很长时间，才证明了出来，所以考完之后就写在书上了)。

       然后，由于神经网络解决感知机的问题，训练过程较为简单，所以我感觉大家其实都写的差不多，都是一种写法，因为，根本没有必要去，写一个runner类进行调用，所以我特意做了可视化，这样也方便比较，并且来看直观(可视化真的弄了好长时间，不过这次学习了常规的描绘边沿的方法，感觉还是很有用的，哈哈哈)。

       好了，下边说有用的，下边是一些证明，大家可以看看(写的确实有点乱，呜呜)

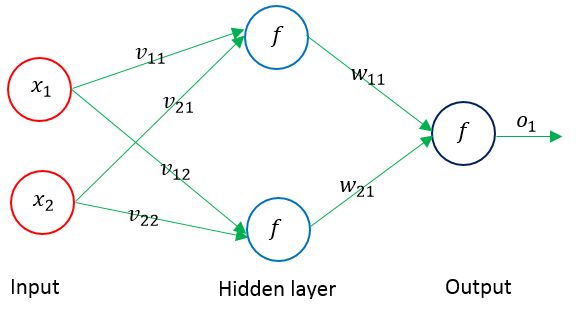
     然后就要，说一说代码的实现了，首先，搭建的神经网络的大致框图为：

     神经网络就是大致按照，下边的架子搭的，也就是一个2个神经元的隐层，最后一个输出。

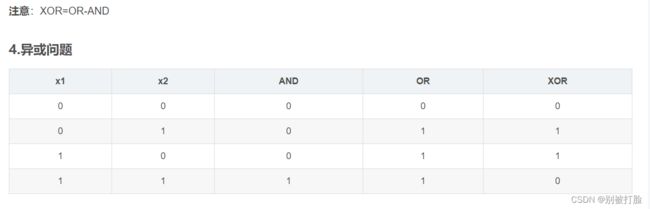
       然后说一下，输入输出的数据，这个从哪来呢，怎么体现异或问题呢，这个从我上边铅笔写的就可以看出，也就是下图中所表现的。）

      由上图可以看出，我们的数据是(0,0)、(0,1)、(1,0)、(1,1)，对应的标签是0,1,1,0。

      然后，解释一下，咱们网络层的构建的公式(其实就是之前博客上解释过的过程)

隐含层的表达式见公式1和公式2所示。

                                                                                                   (1)

                                                                                                    (2)

输出层表达式如公式3所示。

                                                                                                     (3)
 

       下边就是就是代码了(前边我可能有点废话多了，哈哈哈)

4.2.1  网络的构建

# coding=gbk
import torch.nn as nn
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
import math
import numpy as np

from torch.autograd import Variable
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_

        由于我做了一下可视化，所以相较于别人，我用到的库可能相对较多，老师和各位大佬，如果有啥更好的可是化的方法，请多交一交我。

        这个还是我之前说过的问题，注意解码方式，要不然注释有可能会报错，这样弄起来会很麻烦。

# 异或门模块由两个全连接层构成
class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(normal_(w1,mean=0.0, std=1.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(normal_(w2,mean=0.0, std=1.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = nn.ReLU()

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

      这个网络其实就是，咱们上一边博客的网络，我连网络的名都没有改，就是修改了一下激活函数，咱们这个记得激活函数，要用nn.ReLU()，要不然如果用F.relu()的话是会报错的。

      这个问题之前说过好几次了，是函数用法的问题，大家有兴趣的话，去看一看我之前写的博客，帮我批评指正一下。

 4.2.2   参数的设置

# 输入和输出数据
input_x = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
input_x1 = input_x.float()
real_y = torch.Tensor([[0], [1], [1], [0]])
real_y1 = real_y.float()
# 设置损失函数和参数优化函数
net = Model_MLP_L2_V2(2,2,1)
loss_function = nn.MSELoss(reduction='mean')  # 用交叉熵损失函数会出现维度错误
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)  # 用Adam优化参数选不好会出现计算值超出0-1的范围
epochs=2000   #训练次数

       这个就是把数据设置一下，并且设置一下，相关的超参数，这个的设置与调试，在上边博客中有大量的讨论。

 4.2.3  训练模型

# 进行训练
for epoch in range(epochs):
    out_y = net(input_x1)
    loss = loss_function(out_y, real_y1)  # 计算损失函数
    # print('啦啦啦')
    optimizer.zero_grad()  # 对梯度清零，避免造成累加
    loss.backward()  # 反向传播
    optimizer.step()  # 参数更新

        这个就是正常的训练步骤，为了，方便就没有写runner类了。其实，规范的话，最好是写的。

4.2.4   打印训练结果

# 打印计算的权值和偏置
print('w1 = ', net.fc1.weight.detach().numpy())
print('b1 = ', net.fc1.bias.detach().numpy())
print('w2 = ', net.fc2.weight.detach().numpy())
print('b2 = ', net.fc2.bias.detach().numpy())




input_test = input_x1
out_test = net(input_test)
print('input_x', input_test.detach().numpy())
print('out_y', out_test.detach().numpy())

这个就是正常的调用print函数打印一下结果。

w1 =  [[ 1.314425  -2.527302 ]
 [-1.0961039  1.4463567]]
b1 =  [ 0.03252467 -0.15060449]
w2 =  [[0.87763757 0.9123106 ]]
b2 =  [-0.182134]
input_x [[0. 0.]
 [0. 1.]
 [1. 0.]
 [1. 1.]]
out_y [[0.0000000e+00]
 [9.9999440e-01]
 [9.9999964e-01]
 [7.2270632e-06]] 

可以看出，结果非常好。

4.2.5  可视化

# 这里我稍微调整了下plt.contour中的参数，使得结果更好看一点
def plot_decision_boundary(model, x, y):
    x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
    y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
    h = 0.01
    # 绘制网格
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 生成与网格上所有点对应的分类结果
    z = model(np.c_[xx.ravel(), yy.ravel()])
    z = z.reshape(xx.shape)
    # 绘制contour
    plt.contour(xx, yy, z, levels=[0.5], colors=['blue'])
    plt.scatter(x[:, 0], x[:, 1], c=y)
    plt.show()

def plot_network(x):
    x = Variable(torch.from_numpy(x).float())
    x1 = torch.mm(x, net.fc1.weight.T) + net.fc1.bias.T
    x1 = F.relu(x1)
    x2 = torch.mm(x1, net.fc2.weight.T) + net.fc2.bias.T
    out = F.relu(x2)
    out = (out > 0.5) * 1
    return out.data.numpy()




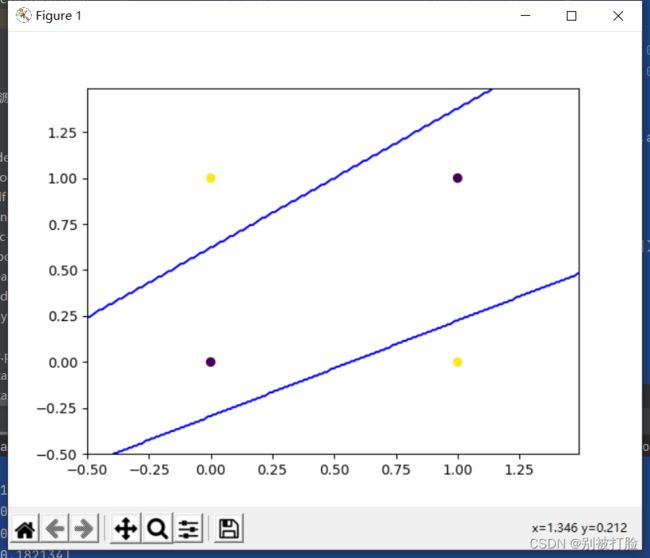
plot_decision_boundary(lambda x: plot_network(x), input_x1.numpy(), real_y1.numpy())

运行结果为：

这个是函数边沿的描绘，这个就可以看出，神经网络的优越性了。

4.2.6 与感知机的比较 

# coding=gbk
import numpy as np
import matplotlib.pyplot as plt

# 载入数据
x_data = np.array([[1, 0, 0],
                   [1, 0, 1],
                   [1, 1, 0],
                   [1, 1, 1]])
y_data = np.array([[-1],
                   [1],
                   [1],
                   [-1]])
# 设置权值,3行1列，取值范围为-1~1
w = (np.random.random([3, 1]) - 0.5) * 2
print(w)
# 学习率
lr = 0.11
# 神经网络输出
out_rs = 0


def update():
    global x_data, y_data, w, lr  # 使用全局变量，当然也可以使用一个return返回
    out_rs = np.sign(np.dot(x_data, w))
    w_c = lr * (x_data.T.dot(y_data - out_rs)) / int(x_data.shape[0])
    w = w + w_c


for i in range(100):
    update()  # 权值更新
    out_rs = np.sign(np.dot(x_data, w))  # 计算当前输出
    print("epoch:", i)
    print("w:", w)
    if (out_rs == y_data).all():  # 如果当前输出与实际输出相当，模型收敛，循环结束（.all是全部相等的意思）
        print("#####################")
        print("finished")
        print("epoch:", i)
        print("#####################")
        break
# 正样本
x1 = [0, 1]
y1 = [1, 0]
# 负样本
x2 = [0, 1]
y2 = [0, 1]

# 计算分界线的斜率以及截距
k = -w[1] / w[2]
b = -w[0] / w[2]
print("k = ", k)
print("b = ", b)

# 绘图，scatter绘点、plot绘制直线
xdata = (0, 5)
plt.figure()
plt.plot(xdata, xdata * k + b, 'r')
plt.scatter(x1, y1, c='b')
plt.scatter(x2, y2, c='y')
plt.show()

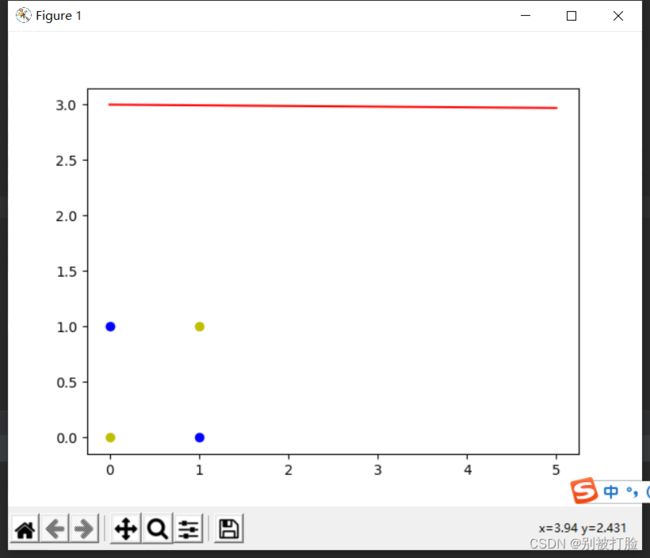
运行结果为：

        从结果中就可以看，神经网络的优越性。可视化之后更为直接，从图像中就可以看出神经网络的优越性。

二、习题4-3 试举例说明“死亡ReLU问题”，并提出解决方法.

    这里先要说一下，什么叫“死亡ReLU问题”

    死亡ReLU问题： ReLU激活函数可以一定程度上改善梯度消失问题，但是ReLU函数在某些情况下容易出现死亡 ReLU问题，使得网络难以训练。这是由于当x<0x<0时，ReLU函数的输出恒为0。在训练过程中，如果参数在一次不恰当的更新后，某个ReLU神经元在所有训练数据上都不能被激活（即输出为0），那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远都不能被激活。

    由于上边说到了，就不得不提一下，梯度消失的问题了，这个下边也会提到。

      梯度消失：其实，最直接的原因就是sigmoid型函数的导数，是小于1的，当层数过多，相乘会越来越趋于零，这就是上课老师说的核心意思，如上图

     好了，废话说完了，我们来看一下，代码实例这个是用ReLU来实现的。

# 定义多层前馈神经网络
class Model_MLP_L5(torch.nn.Module):
    def __init__(self, input_size, output_size, act='sigmoid'):
        super(Model_MLP_L5, self).__init__()
        self.fc1 = torch.nn.Linear(input_size, 3)
        normal_(self.fc1.weight,mean=0.0, std=0.01)
        constant_(self.fc1.bias,val=-8.0)
        self.fc2 = torch.nn.Linear(3, 3)
        normal_(self.fc2.weight,mean=0.0, std=0.01)
        constant_(self.fc2.bias,val=-8.0)
        self.fc3 = torch.nn.Linear(3, 3)
        normal_(self.fc3.weight,mean=0.0, std=0.01)
        constant_(self.fc3.bias,val=-8.0)
        self.fc4 = torch.nn.Linear(3, 3)
        normal_(self.fc4.weight,mean=0.0, std=0.01)
        constant_(self.fc4.bias,val=-8.0)
        self.fc5 = torch.nn.Linear(3, output_size)
        normal_(self.fc5.weight,mean=0.0, std=0.01)
        constant_(self.fc5.bias,val=-8.0)
        # 定义网络使用的激活函数
        if act == 'sigmoid':
            self.act = F.sigmoid
        elif act == 'relu':
            self.act = F.relu
        elif act == 'lrelu':
            self.act = F.leaky_relu
        else:
            raise ValueError("Please enter sigmoid relu or lrelu!")
    # 初始化线性层权重和偏置参数
    def init_weights(self, w_init, b_init):
        # 使用'named_sublayers'遍历所有网络层
        for n, m in self.named_sublayers():
            # 如果是线性层，则使用指定方式进行参数初始化
            if isinstance(m, nn.Linear):
                w_init(m.weight)
                b_init(m.bias)
 
    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        outputs = self.act(outputs)
        outputs = self.fc3(outputs)
        outputs = self.act(outputs)
        outputs = self.fc4(outputs)
        outputs = self.act(outputs)
        outputs = self.fc5(outputs)
        outputs = F.sigmoid(outputs)
        return outputs

    运行结果为：

The weights of the Layers：
-->name: fc1.weight  -->grad_value: tensor([[0., 0.],
        [0., 0.],
        [0., 0.]])
---------------------------------
-->name: fc1.bias  -->grad_value: tensor([0., 0., 0.])
---------------------------------
-->name: fc2.weight  -->grad_value: tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
---------------------------------
-->name: fc2.bias  -->grad_value: tensor([0., 0., 0.])
---------------------------------
-->name: fc3.weight  -->grad_value: tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
---------------------------------
-->name: fc3.bias  -->grad_value: tensor([0., 0., 0.])
---------------------------------
-->name: fc4.weight  -->grad_value: tensor([[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]])
---------------------------------
-->name: fc4.bias  -->grad_value: tensor([0., 0., 0.])
---------------------------------
-->name: fc5.weight  -->grad_value: tensor([[0., 0., 0.]])
---------------------------------
-->name: fc5.bias  -->grad_value: tensor([-0.5106])
---------------------------------
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.52500

使用Leaky ReLU进行模型训练

将激活函数更换为Leaky ReLU进行模型训练，观察梯度情况。代码实现如下：

# 重新定义网络，使用Leaky ReLU激活函数
model =  Model_MLP_L5(input_size=2, output_size=1, act='lrelu')
 
# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
 
# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev],
            num_epochs=1, log_epochps=None,
            save_path="best_model.pdparams",
            custom_print_log=custom_print_log)

运行结果为：

The weights of the Layers：
-->name: fc1.weight  -->grad_value: tensor([[-2.2568e-16,  3.5508e-17],
        [ 1.1090e-16, -1.7448e-17],
        [ 1.9872e-16, -3.1266e-17]])
---------------------------------
-->name: fc1.bias  -->grad_value: tensor([-2.2717e-16,  1.1163e-16,  2.0003e-16])
---------------------------------
-->name: fc2.weight  -->grad_value: tensor([[-1.6787e-14, -1.6798e-14, -1.6811e-14],
        [ 1.1792e-14,  1.1799e-14,  1.1809e-14],
        [-1.3686e-13, -1.3695e-13, -1.3706e-13]])
---------------------------------
-->name: fc2.bias  -->grad_value: tensor([ 2.1013e-13, -1.4761e-13,  1.7131e-12])
---------------------------------
-->name: fc3.weight  -->grad_value: tensor([[-6.6518e-10, -6.6498e-10, -6.6517e-10],
        [-1.2666e-10, -1.2662e-10, -1.2666e-10],
        [ 1.0642e-09,  1.0639e-09,  1.0642e-09]])
---------------------------------
-->name: fc3.bias  -->grad_value: tensor([ 8.3144e-09,  1.5832e-09, -1.3302e-08])
---------------------------------
-->name: fc4.weight  -->grad_value: tensor([[-6.6640e-07, -6.6628e-07, -6.6627e-07],
        [-2.9873e-06, -2.9867e-06, -2.9867e-06],
        [-5.7090e-06, -5.7080e-06, -5.7080e-06]])
---------------------------------
-->name: fc4.bias  -->grad_value: tensor([8.3289e-06, 3.7336e-05, 7.1353e-05])
---------------------------------
-->name: fc5.weight  -->grad_value: tensor([[0.0401, 0.0401, 0.0401]])
---------------------------------
-->name: fc5.bias  -->grad_value: tensor([-0.5012])
---------------------------------
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.55000
[Train] epoch: 0/1, loss: 4.011898994445801 

       从输出结果可以看到，将激活函数更换为Leaky ReLU后，死亡ReLU问题得到了改善，梯度恢复正常，参数也可以正常更新。但是由于 Leaky ReLU 中，x<0x<0 时的斜率默认只有0.01，所以反向传播时，随着网络层数的加深，梯度值越来越小。如果想要改善这一现象，将 Leaky ReLU 中，x<0x<0 时的斜率调大即可。 
      下边说一下我的理解，因为我尝试过输出，好几前千次的结果，所以在这说一下总结。(也是根据老师上课讲的)

       dead relu problem是一个动态的问题，而并不是一个永久性问题，只要不是所有输入都小于0，神经元就可以保持活跃，权重可以更新，网络可以继续学习。因此，dead的relu也是可以复活的。

       之所以可能会出现较长的dead relu problem主要原因在于前面提到过的，relu activation之前的layer的梯度得不到更新，因此relu activation之前的layer的权重保持不变，而我们的输入数据本身是不会发生变化的，这就导致了在每一个epoch中，输入的数据不变还是training数据集，relu activation之后的计算结果一直是0； 

        如果要彻底避免dead relu problem，则我们使用prelu，leaky relu 等relu的简单变体就可以了。但是老师上课说了一句话，并没有任何证明，来证明后边的变体，在实际操作是会明显优于relu，有时还并不会优于，所以大家一定要注意这个，不要像我以前一样，经验主义。

       最后，放一下各个函数的图像，方便大家理解

三、习题4-7 为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化? 

首先，咱们来看一下神书花书的原文

 

神书花书中7.1节，7.5节都写到了中写到：

1. “在神经网络中，参数包括每一层仿射变换的权重和偏置，我们通常只对权重做惩罚而不对偏置做正则惩罚”
2. “正则化偏置参数可能会导致明显的欠拟合”

可以通过如下图来理解，例如我们想要通过wx+b的仿射变换拟合下列散点：

 

• 如果同时对权重w和偏置b进行正则，那么拟合的直线很有可能是一条斜率较小、经过原点的直线，这样会导致欠拟合问题（正如书中所说）；
• 相对的，如果只对w进行正则而不对b进行正则，即使w很小（斜率较小），也可以通过调整偏置b（即平移）来使得直线较好的拟合数据点，从而避免了欠拟合问题。

上课老师也是说过的，并且以前我也问过老师，老师的大致意思是：

       这个正则化其实是一种惩罚策略，是为了防止过拟合的，如果把所有的参数都进行惩罚的话，这样惩罚会太过，会导致欠拟合，并且参数是没有必要进行惩罚的。(我感觉这么理解是非常直观的，好理解的）

       达哥以前讲的时候，没注意，确实是我的问题，呜呜。

 下边有个从数学上解释的，大家要是有兴趣看一看吧(感觉不直观明白，达哥和老师都是我上边写的意思，神书花书也是有数学推导的比较直观，拜一拜）

      从贝叶斯的角度来讲，正则化项通常都包含一定的先验信息，神经网络倾向于较小的权重以便更好地泛化，但是对偏置就没有这样一致的先验知识。另外，很多神经网络更倾向于区分方向信息（对应于权重），而不是位置信息（对应于偏置），所以对偏置加正则化项对控制过拟合的作用是有限的，相反很可能会因为不恰当的正则强度影响神经网络找到最优点。

四、习题 4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令 w= 0, = 0？

    首先，咱们先说一下这个问题叫什么，然后在举个例子，然后咱们再看一下代码，然后咱们说一下解决方案。

    首先，这个问题的名字是：

    如果对每一层的权重和偏置都用0初始化，那么通过第一遍前向计算，所有隐藏层神经元的激活值都相同；在反向传播时，所有权重的更新也都相同，这样会导致隐藏层神经元没有差异性，出现对称权重现象。

     那么，咱们像反向传播那样，代数试试。

     设有一个多层感知机模型，假设输出层只保留一个输出单元o1o_1o1，且隐藏层使用相同的激活函数。如果将每个隐藏单元的 参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。

     在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代 也是如此。在这种情况下，无论隐藏单元有多少，隐藏层本质上只有一个隐藏单元在发挥作用。

     这样就比较清楚了，然后咱们看一下代码。

class Model_MLP_L2_V4(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        # 使用'paddle.nn.Linear'定义线性层。
        # 其中第一个参数（in_features）为线性层输入维度；第二个参数（out_features）为线性层输出维度
        # weight_attr为权重参数属性，这里使用'paddle.nn.initializer.Normal'进行随机高斯分布初始化
        # bias_attr为偏置参数属性，这里使用'paddle.nn.initializer.Constant'进行常量初始化
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1 = torch.empty(hidden_size,input_size)
        b1=  torch.empty(hidden_size)
        self.fc1.weight=torch.nn.Parameter(constant_(w1,val=0.0))
        self.fc1.bias=torch.nn.Parameter(constant_(b1,val=0.0))
        self.fc2 = nn.Linear(hidden_size, output_size)
        w2 = torch.empty(output_size,hidden_size)
        b2 = torch.empty(output_size)
        self.fc2.weight=torch.nn.Parameter(constant_(w2,val=0.0))
        self.fc2.bias=torch.nn.Parameter(constant_(b2,val=0.0))
        # 使用'paddle.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = F.sigmoid
 
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
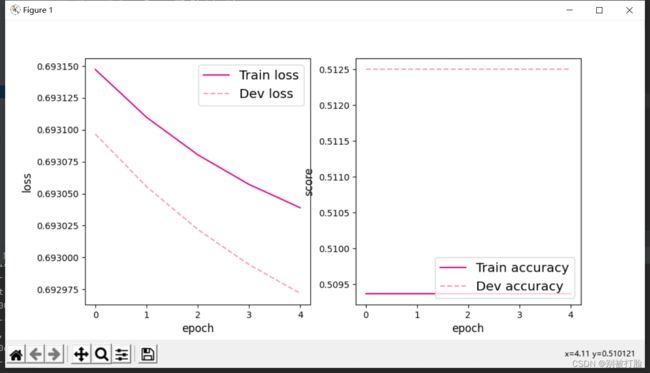
        return a2

运行结果为：

        从输出结果看，二分类准确率为50%左右，说明模型没有学到任何内容。训练和验证loss几乎没有怎么下降。

        为了避免对称权重现象，可以使用高斯分布或均匀分布初始化神经网络的参数。

解决方案

       因此，通常对神经网络的模型参数，特别是权重参数进行随机初始化。随机初始化模型参数的方法有很多，可以使用正态分布 的随机初始化方式。

       还有一种比较常用的随机初始化方法叫做Xavier随机初始化。假设某全连接层的输入个数为a，输出个数为b，Xavier随机初始 化将使该层中权重参数的每个元素都随机采样于均匀分布，它的设计主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数影响，且每层梯度的方差也不该受该层 输出个数影响。

       咱们之前试了第一种，但是看达哥的视频，达哥说了后边的更好一点，那必然是后边的更狠一点了呀。

五、习题4-9 梯度消失问题是否可以通过增加学习率来缓解？

       首先，这个问题我看了好多资料，然后达哥没有重点讲过，他只是稍微说过一点，而且我之前，因为不敢调lr，出现了问题，所以也和老师涉及到过，所以先说一下我的理解。

       首先，直观上说他是可以缓解的，但也只是缓解，因为从直观上看，迭代的时候是lr乘以梯度，所以如果梯度过小，增大lr会有可能稍微缓解，但是这种情况下，会导致在寻找最小值上出问题，这就和之前说过的情况正好相反了(很有可能是从全局最小，变到了局部最小）。

       并且梯度并不会因此而增大，这就会导致每次学到的，特征会非常少，会导致网络极难训练，因为根本的原因，并没有解决，所以我说只会是稍微的缓解，而并不会真正的解决问题。

        然后我看资料，感觉确实有用，下边是一个英文版的(还是老师说的对呀，这些好的文章好多都是英文版的

最后，得出的结论是：

        不行，因为梯度消失不是指梯度太小，而是指的是梯度在最后一层往前传的过程中不断减小，这个消失，指的是最底层的梯度和最高层的梯度量级的差别。

        如果你增大了lr，底层的学习可能确实更加有效了，高层的梯度就可能炸了。

        那能不能每层设置不一样的lr呢，当然可以，adagrad就是这么做的，也确实有一定效果。(这个上边文章中写的)

---

总结

      首先，先说一下感受，终于有时间拿出一个下午来写这个了，查了好多东西，写了一下午，虽然感觉很累，但是我相信这都是值得的(并且这写完感觉真的很爽，解决了好多问题，哈哈哈)

      其次，说一下，遇到的问题，我在写可视化的时候，写了好长时间，一个是注意matplotlib库，这个库不能直接输入tensor变量，所以这里又要重写网络，学到了常用的方法。(据说是经典网络的常用方法，哈哈哈）

        可以看一下，下边的链接，结合我写的，对应就好明白了

可视化技巧：分类问题中的决策面画法 (直观理解plt.contour的用法)_此人姓于名叫罩百灵的博客-CSDN博客_plt.contour       

      

       然后，说一下，我发现的问题，希望老师和各位大佬可以教我一下，我可视化在画图时发现，如果全用relu作为激活函数，效果并不是太好，但是可以第一个用relu函数，第二个用sigmoid函数，损失函数用交叉熵(也可以用均方误差，这个影响不太大,几乎没区别)，这样效果会好一点，但是也不能保证百分之百训练正确，但是出错率会比之前小，也就是会比之前全用relu()，好一点，因为，我后来想了想，其实这个有点偏向与分类的问题。

     

        然后，说一下，感觉之前好多都没想具体过，也就是没啥感觉，就是当时可能听达哥说过，但是没啥感觉，没有注意到，就像这次b的正则化那个，要是这次不写就快忘了。

       其次，又深入了一下之前写过的那几个问题，又看了好多新的理解，感觉又有了新的理解。

       最后，终于变成中风险了，终于快要线下见面了，这几天统计的表也少了不少，终于快要和老师线下见面了(哈哈哈)。

       最后，当然是谢谢老师，感谢老师在学习和生活上的关心(哈哈哈)