Tensor Methods in Computer Vision and Deep Learning学习笔记

学习笔记_边凯昂

第一章 Tensor Methods in Computer Vision and Deep Learning

---

前言

  这是一篇关于张量在计算机视觉和深度学习中的应用的论文。本文回顾了represent learning（表征学习）和深度学习特别是在视觉数据分析和应用中的张量和张量方法，还关注了张量方法逐渐增加给深度学习架构和计算机视觉应用中的影响。
  对于这篇论文，前面比较基础的数学概念我相对熟悉，但后面一些数学模型以及张量方法的应用读不太懂。

---

一、介绍

  张量是矩阵的推广，矩阵是二阶张量（行和列），张量也可以看作是矩阵表示函数的推广。张量的阶数是处理其元素所需的索引的数量。张量被用来表示和分析隐藏在多维数据中的信息，如图像和视频，或捕获和利用向量值变量之间的高阶相似性或依赖性。张量可以展示多维可视化数据，在计算机视觉和深度学习中有着重要的应用。

1.视觉数据中的张量结构

视觉数据是一种多维数据，而张量结构是其中两种固有形式：
A.视觉测量值的张量结构
B.图像形成过程中的潜在张量结构
  多维视觉数据样本需要被扁平成非常高维的向量，在那里，自然拓扑结构和不同模式（例如，空间和时间）之间的依赖性丢失；除了结构损失外，当在训练基于矩阵的机器学习模型中使用高维向量时，在给定的精度水平内估计任意函数（或机器学习模型的参数）所需的数据样本数量随数据维数呈指数增长。这种现象被称为维数的诅咒。

2.计算机视觉表征学习中的张量方法

目的：为了减轻维度的诅咒而不丢弃它们的结构，恢复潜在因素在视觉数据和灵活足以适应大量的结构约束和正则化；表现为降维、聚类和数据压缩。
  深度学习模型通过局部统计来利用数据的统计特性，如平稳性（例如，移位不变性）和组合性（例如，图像的层次结构），这些都存在于视觉数据中。这些特性被卷积体系结构所利用，它们由交替的多维卷积层、点向非线性函数(如ReLU)、下采样（池化）层组成，同时也包含张量结构的全连接层。在深度神经网络中使用多维卷积可以提取跨图像域共享的局部特征，这大大减少了可学习参数的数量，从而减轻了维数诅咒的影响——而不牺牲近似目标函数的能力。

3.基于计算机视觉的深度学习体系结构中的张量方法

  尽管深度神经网络的组成结构减轻了维数的诅咒，但深度学习模型通常被过度参数化，涉及大量（通常是数千万甚至数十亿）的未知参数。张量分解可以显著减少深度模型中未知参数的数量，进一步减轻维数的诅咒。（应用于神经网络层的权值来压缩它们；保留和利用数据中的拓扑结构，同时产生简约的模型）
  随机神经网络的张量分解能有效对抗对抗性攻击和各种类型的随机噪声方面。

二、张量和矩阵代数的基本原理

1.相关记号

描述了一些记号（标量、矩阵、实数、整数集等）
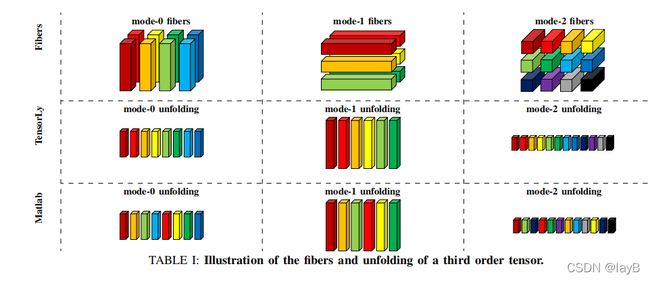
Fibers ：通过固定除一个指数以外的所有指数而得到的（几维就表明有几个索引有几个Fibers模式）
如图一个342规模的3维张量通过控制其中两个指数，可以被分为3种Fibers。下面分别是被分为42，32，34的三种Fibers。
下面Tensorly 和Matlab听学长说，目前没有直接处理张量的软件，所以下面是张量被处理成不同fibers然后被两种软件解析不同Fibers的方式。

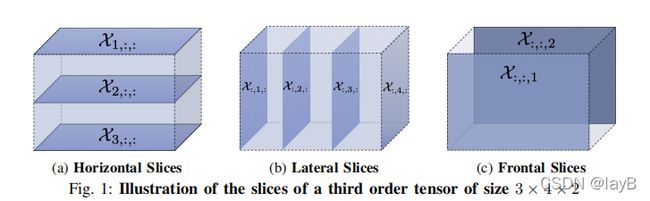
Slices ：通过固定其中一个指数得到的
比如一个34*2的张量有3种切片模式（几维就表明有几个索引有几个Slices模式）

2.将张量转换为矩阵和向量

张量展开：张量展开对应于张量的纤维作为矩阵的列的重新排列，且张量的展开不唯一，随Fibers的顺序变化。
张量向量化：一个N维的张量可以映射到N个向量

3.矩阵和张量的积

Kronecker积：

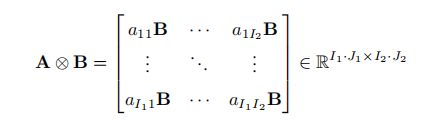
比如一个22 的和33的矩阵的Kronecker积是一个6*6的矩阵

Khatri-Rao 积：要求两个矩阵有相同的列

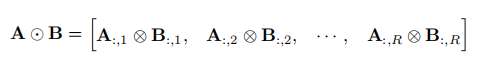
Hadamard积：要求两个矩阵同行同列

外积：N维向量的外积
  被定义了一个一级的n阶张量

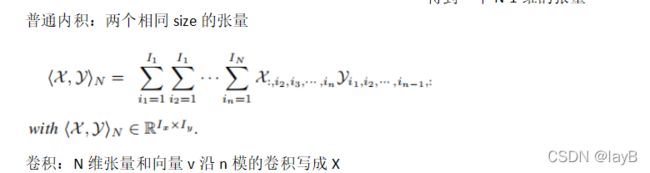
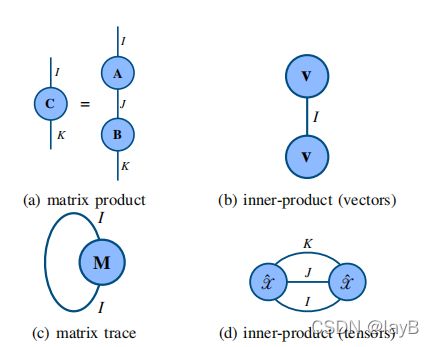
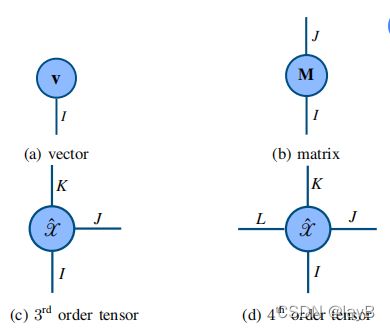
4.张量图

用无向图表示张量的代数运算，顶点表示张量，它的边缘是该张量的模态。

一个张量有几条线就有几个索引有几维

5. 矩阵秩：化简后有几个线性无关的向量矩阵秩就是几

6. 范式

三、现有的计算工具和必要的基础设施的概述

  讨论计算机视觉和深度学习的必要基础软硬件。介绍了可用的张量代数软件包和TensorLy库。

四、张量分解的表征学习（这节涉及具体的数据模型，不是很懂）

1.矩阵分解和表征学习

  视觉对象的外观（例如，照明和姿态的变化，刚性和刚性的变形、刚性和非刚性的变形）、图像结构、语义和噪声，真实世界的视觉数据表现出复杂的可变性。因此，有用的信息被隐藏在高维的视觉测量中。而表征学习寻求提取有用的信息从这样的高维数据通过简单，低维表示。（用低秩和稀疏性来度量）
  矩阵分解用于从高维数据样本中学习简洁、低维的表征.

  此式子表明矩阵X可以表示成两个子矩阵的乘积；但是U1 U2是不唯一的。因为存在可逆矩阵P使得X=U1PP^-1 *U2^T

2.张量分解：三个最基本的张量分解模型

Canonical-Polyadic (CP)分解：将X分解为R秩1张量的和
Tucker分解
列车张量

3.鲁棒张量分解

  为了从噪声测量中恢复一个循环张量，假设存在可能具有较大幅度的非高斯噪声。这些异常值只影响一小部分的测量值，因此，噪声被认为是稀疏的。

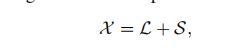
  其中X是一个n阶数据张量，通常由沿张量的第N个模式排列一组N−1阶张量数据样本组成。L和S分别是未知的n阶张量，分别解释了低秩张量和稀疏噪声。

4.张量分量分析：将分量分析的概念扩展到由高阶张量表示的数据

  不同的张量分量分析方法可以作为约束优化问题的不同解。

5.张量结构的稀疏编码

  稀疏编码（或字典学习）方法是许多视觉信息处理任务中的核心。一个数据矩阵X∈RI×M在其列中包含了大小为√I×√I的矢量化图像补丁，而不是数据样本。

6.张量回归

  除了学习表征外，低秩张量分解有助于减少张量回归模型的参数，防止过拟合。张量回归模型的发展过程将线性回归推广到高阶张量。

五、在深度学习（神经网络体系）利用张量方法的研究

六、张量在计算机视觉中的相关应用

1.视觉数据中提取多种潜在变异因素

  在计算机视觉中，考虑视图和假定视觉对象分类问题，需要对不同视角捕获的视觉对象进行分类和处理。需要设计或学习不变的数据表示来查看和姿态变化，同时捕获有关对象类别的判别信息，运动结构（旨在从二维图像序列中估计三维结构）是另一个需要分离多个因素的计算机视觉任务。更具体地说，我们需要解开形状和运动因素，然后利用它们来重建三维视觉物体。人脸编辑和说话人脸合成是需要操纵多个潜在变量的进一步问题。
  用两种不同的方法进行了多因素分析。第一种方法将视觉数据平化为向量，然后根据其形成的因素将向量排列成一个张量，为后续分析准备数据。第二种，最近的方法假设在基于深度自动编码器的架构中有一个张量结构的潜在空间。
  我认为，用低维的数据样本去估计高维数据样本的特征从而展现物体的结构，即需要从视觉对象中提取有一点低维的数据来，根据条件删去杂糅的数据。

2.通过张量分量分析进行降维

3.逆问题中的张量法

  通过将视觉表示为张量，解决逆问题的模型利用低秩张量分解(第IV-B节)，或依赖鲁棒变量来估计低秩张量，该张量形成了一个基础，形成了可以推断或去噪缺失数据的基础。

4.视觉分类的张量回归

  低秩张量回归模型非常适合于大规模视觉数据的分类（如人脸和身体图像和视频，以及高光谱和医学图像）
  所以一个高秩的张量模型可以通过低秩张量回归模型进行数据的分类。

5.利用张量分解进行深度网络参数化

七、实际挑战、建议

  张量方法是从多维数据中学习的方便工具，也是在深度神经网络中注入更多结构的方便框架，利用冗余来获得更紧凑的模型，并增加鲁棒性。但仍有一些挑战目前可能会阻碍它们得到更广泛的采用。如排名选择、哪一种分解、训练紧张化的深度神经网络等。

---

总结

  看了这篇论文，首先我了解了什么是张量，张量是矩阵的推广，是多维的数据结构，用来表示和分析隐藏在多维数据中的信息。张量结构和张量方法在计算机视觉和深度学习中有重要运用。由于其中具体的应用情况，训练基于矩阵的机器学习模型中使用高维向量时，张量的信息和规模是巨大的、杂糅的。所以需要根据特定的需要对张量进行分解，提取出有用的张量来减轻维数的诅咒，保留和利用数据中的拓扑结构，同时产生简约的模型。
  文中第二部分引用其他综述阐述了张量和矩阵代数的基本原理。有相关记号，张量分别对于Fibers和Slices两种不同方式的展开，张量转换矩阵和向量，还有一些矩阵张量积，和张量图用于张量的计算。
  文中第四部分阐述张量分解在表征学习的应用，不是很懂，大致可能是把高维的数据样本根据需要提取出能体现出物体特征的低维数据。是一种高维、杂糅到低维、简约样本的转换，而其中的维数可以用秩和稀疏性来度量。后面列举了三种张量分解的模型，还要张量分量分析，稀疏编码和张量回归。这些内容有待进一步学习。
  由于张量的数据结构，在计算机视觉中有广泛应用。视觉数据中提取多种潜在变异因素，通过张量分量分析进行降维，逆问题中的张量法，利用张量分解进行深度网络参数化，这些大部分都是通过原有的高维数据样本根据特定约束转化到低秩张量，利用低秩张量的优点进行数据分析，我觉得原理都差不多，应用大同小异。
  但对于张量的具体分解和根据约束将高阶张量如何降维等内容还尚不明白；对深度学习和计算机视觉也不是很了解。